数据结构——树_亲节点子节点-优快云博客

本文为个人学习笔记，如有错误，欢迎批评指正，我们一起学习呀。如有侵权，请联系删除。

今日格言：今天应做的事没有做，明天再早也是耽误了。

树

树的概念

树是一种非线性的结构，它是由n个节点组成的一个具有层次关系的集合。为什么把它叫作树呢？因为你一眼看去，它就像是一棵倒挂的树，也就是根朝上，叶朝下。

根节点：根节点是一个特殊的节点，因为它没有直接前驱。

除了根节点之外，其余节点都被分为M个不相交的集合，每一棵子树的根节点有且仅有一个前驱，有0个或者多个后继。每棵树都能看成都能看成根和它的子树构成。因此，树是递归定义的。

所以在树中，子树都是不相交的，图中的标出的树，其根节点都不止一个前驱，不符合数的定义

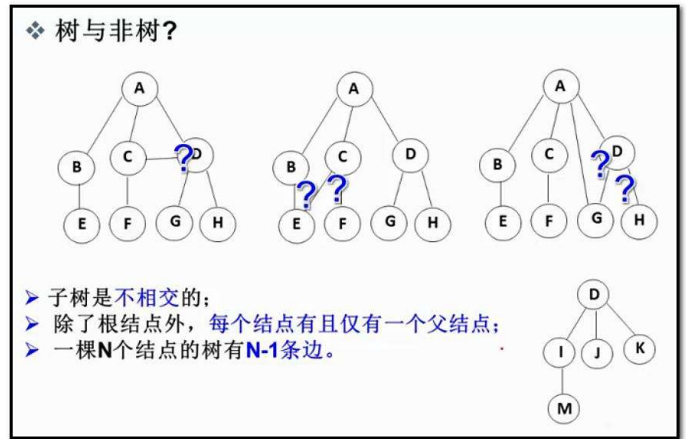
树的结构（其实下面的概念不用死记硬背，联系实际就很容易理解啦）

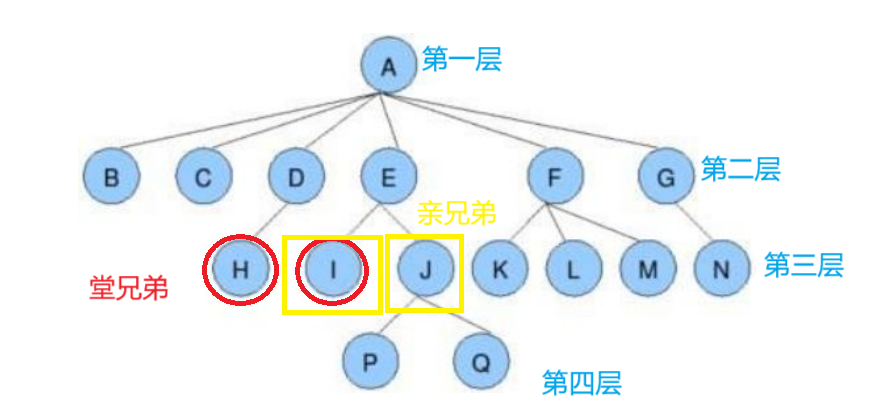
节点的度：一个结点含有子树的个数称为这个节点的度，比如图中的A的度是6（其实我们也可以直接看它有多少条线延伸出去）。

树的度：树的度就是在这棵树中最大的节点的度。在这棵树中，树的度为6.

叶节点（终端结点）：度为0的节点即为叶节点。

父节点（双亲节点）：一个节点含有子节点，那么这个点就称为该子节点的父节点，A是B的父节点

子节点（孩子节点）：与父节点相对应，一个节点含有的子树的根节点称为该节点的子节点，B是A的子节点

兄弟节点：具有相同父节点的节点互为兄弟节点，B和C是兄弟节点

堂兄弟节点：双亲节点在同一层上的节点互为堂兄弟结点，H和I是堂兄弟节点。

这里要区分一下兄弟节点和堂兄弟节点，大家也可以联想一下实际，虽然说亲戚关系的区分总是让人头痛，但是你的亲兄弟和堂兄弟还是很好区分的吧

节点的层次：从根定义开始，根为第一层，以此类推

树的高度（深度）：树中节点的最大层次，该树的高度为4

结点的祖先：从根到该节点所经的分支上的所有节点，所有A是所有节点的祖先

子孙：以某节点为根的子树中任一节点都成为该节点的子孙，所有节点都是A的子孙

森林：由m棵互不相交的的多棵树的集合称为森林

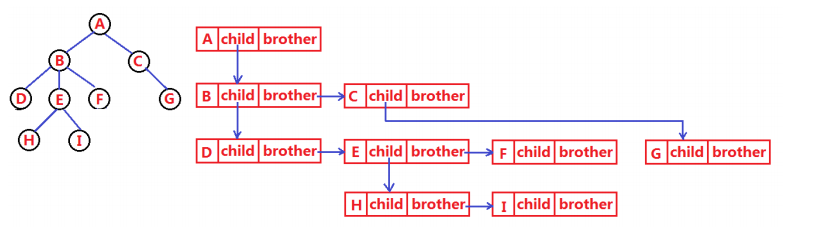
树的表示方法

这里只介绍一种——孩子兄弟表示法

下面是代码形式

typedef int DataType;
struct Node
{
 struct Node* _firstChild1; // 第一个孩子结点
 struct Node* _pNextBrother; // 指向其下一个兄弟结点
 DataType _data; // 结点中的数据域
}

下面是图像，能更清楚的了解这种方法的表示方式

一般使用最多的就是二叉树，下面让我们一起来了解二叉树吧

二叉树

概念：
一棵二叉树是节点的一个有限集合，该集合或者为空，或者是由一个根节点加上两棵左右子树的二叉树构成，这里需要注意的是，子树在左边和在右边是不同的情况，不然我们为什么要多此一举，给他们都起一个名字呢

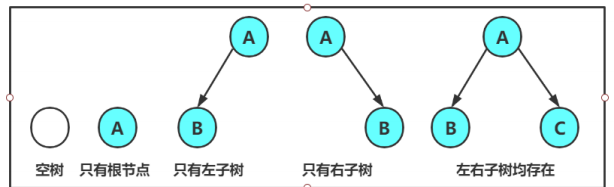
二叉树的特点：
从上面的图中我们也可以看出

（1）每个节点最多有两棵子树，不存在度大于2的树（其实二叉树挺像支持计划生育的树）

（2）二叉树的子树有左右之分，所以子树的顺序不能颠倒

特殊的二叉树

满二叉树：

树的每一层节点数都达到最大值，即每一层都是满的，那么这棵树可以称为满二叉树。

完全二叉树：

完全二叉树是效率很高的树，对于深度为k，有n个节点的二叉树，当且仅当其每一个节点都与深度为k的满二叉树中编号从1~n的节点一一对应时称为完全二叉树。上面是它的概念，我的理解就是除了最后一层外，其余都是满二叉树，最后一层节点是从左到右按顺序排列的

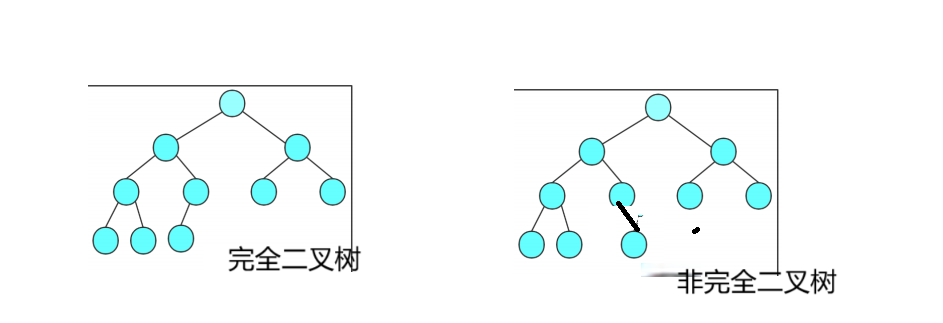
满二叉树其实是特殊的完全二叉树

二叉树的性质

ps:二叉树的性质在做题中应用还是很多的，大家要记住哦

（1）若规定根节点的层数为1，那么一棵非空二叉树的第i层上最多有 2^（i-1）个节点，其实最大的情况就是完全二叉树的情况

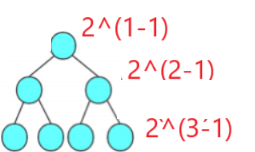
（2）若规定根节点的层数为1，那么深度为h的二叉树的节点个数为2^h-1（即为等比数列求和）

（3）对于任何一棵二叉树，如果度为0的节点个数为n0，度为2的节点个数为n2，那么n0=n2+1，对于完全二叉树而言，度为1的节点个数最大为1。

（4）若规定根节点的层数为1，具有n个节点的满二叉树深度为h=log（n+1）

（5）对于有n个节点的完全二叉树，如果按从上到下从左至右的数组顺序对所有节点从0开始编号，则对序号为i的节点：

a.i>0,起父节点的序号为（i-1）/2；i=0,无父节点

b.2*i+1<n，左孩子：2*i+1

c.2*i+2<n,右孩子，2*i+2

二叉树的存储结构：

顺序存储

顺序存储结构就是用数组来储存，但是数组一般适用于完全二叉树，不然会造成空间的浪费。

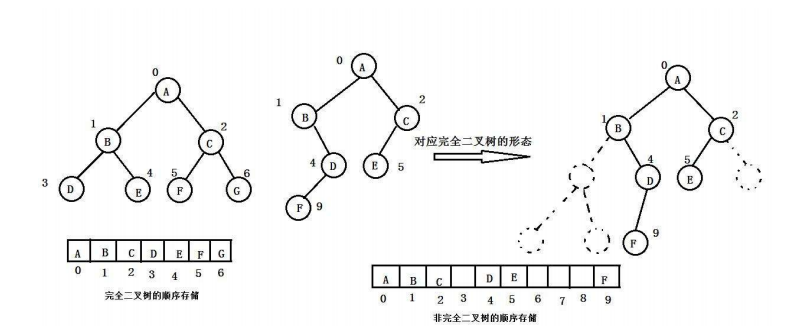
链式存储结构

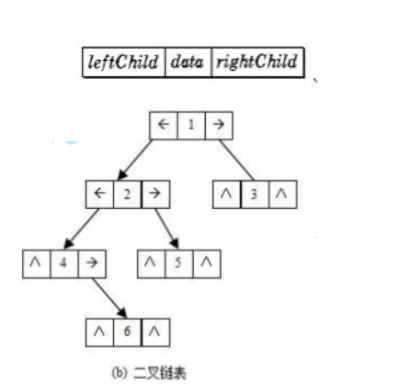
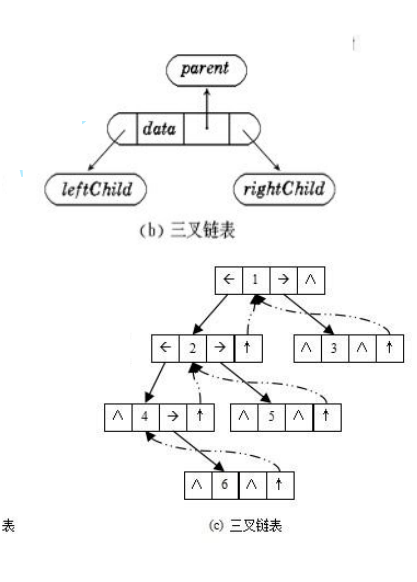
通常情况下，链表中的每一个节点都是由三个域组成，数据域和左右指针域，用左右指针分别表示左右孩子所在链节点的存储地址。链式存储分为二叉链和三叉链。

二叉链

代码表示

typedef int BTDataType;
// 二叉链
struct BinaryTreeNode
{
    struct BinTreeNode* _pLeft; // 指向当前节点左孩子
    struct BinTreeNode* _pRight; // 指向当前节点右孩子
    BTDataType _data; // 当前节点值域
}

图形表示

三叉链

代码表示

// 三叉链
struct BinaryTreeNode
{
 struct BinTreeNode* _pParent; // 指向当前节点的双亲
 struct BinTreeNode* _pLeft; // 指向当前节点左孩子
 struct BinTreeNode* _pRight; // 指向当前节点右孩子
 BTDataType _data; // 当前节点值域
}；

图形表示

堆

堆是一棵完全二叉树。堆分为大堆和小堆，关于大堆和小堆的定义这里就不说了，我说说自己的理解（如有理解不到位的地方，请指出）。

大堆：

根节点总是最大的完全二叉树，是一个大堆

小堆：

与大堆相对应，根节点总是最小的完全二叉树，是一个小堆

堆的实现

我们现在已经知道了堆是一棵完全二叉树，并且完全二叉树可以用数组来表示，那么堆就用数组储存。所以定义了三个变量，分别是存储数据的数组a，数组元素个数size以及数组容量大小capacity，之所以定义size和capacity是为了后面插入数据是扩容方便。

1.堆的初始化

代码表示

void HeapInit(HP* php) {
	assert(php);
	php->size = 0;
	php->capacity = 4;
	HeapDataType* a = (HeapDataType*)malloc(sizeof(HeapDataType)*4);
	if (a == NULL) {
		printf("error\n");
		return;
	}
	
	php->a = a;

}

2.堆的销毁

对于堆的销毁，我们只需要将数组的空间释放，并将指针置空，空间和元素个数置零即可。

代码表示

void HeapDestory(HP* php) {
	assert(php);
	php->size = php->capacity = 0;
	free(php->a);
	php->a = NULL;
}

3.堆的判空

对于堆的判空，我们可以直接利用之前设置的变量size来判断是否为空，通过size，我们就可以知道这个数组里面是否还有元素

bool HeapEmpty(HP* php) {
	assert(php);
	return php->size == 0;
}

4.判断堆中的数据个数

这里和堆的判空类似，我们可以直接通过size得出数组中还剩下多少数据

代码表示

int HeapSize(HP* php) {
	assert(php);
	return php->size;
}

5.取堆顶的元素

因为堆是按照数组存储的，所以我们只需要返回数组中下标为0的元素即可

HeapDataType HeapTop(HP* php) {
	assert(php);
	return php->a[0];
}

6.堆的插入

堆的插入就上点难度了

step 1：将所要插入的数据插入到数组的末端（尾插）；

step 2：调整堆中数据，是其符合大堆或者小堆的要求（我们插入数据时，可能运气超好，插入数据后依旧满足要求。但是，我们不能全靠运气啊，还是要有应对特殊情况的能力的）；

因此这里就要用到向上调整法（从最后一个非叶子节点开始调整），这里以小堆为例：

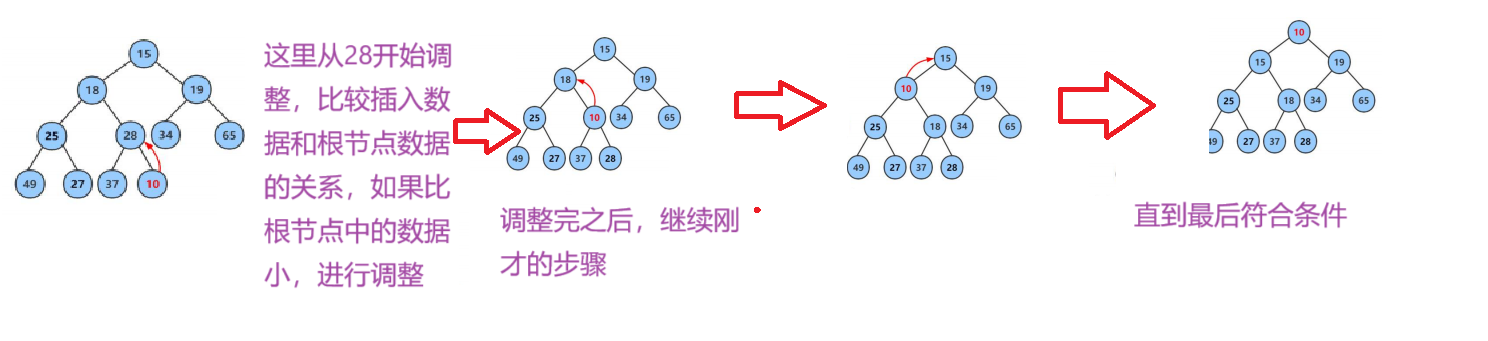
那么我们现在来看看代码是如何实现的吧

void AdjustUp(HeapDataType* a, int child) {
	int parent = (child - 1) / 2;//这里运用了二叉树的性质哦，不记得的话可以往上翻翻
	while (child > 0) {
		if (a[child] < a[parent]) {
			HeapDataType temp = a[child];
			a[child] = a[parent];
			a[parent] = temp;
			child = parent;
			parent = (child - 1) / 2;
		}
		else {
			break;
		}
	}
}

准备工作完成后，我们现在就可以正式开始插入过程啦！

代码表达

void HeapPush(HP* php, HeapDataType x) {
	assert(php);
	//插入数据前我们还得判断数组是不是已经满了，如果满了，则需要扩容
	if (php->size == php->capacity) {
		HeapDataType* temp = (HeapDataType*)realloc(php->a, sizeof(HeapDataType) * php->capacity * 2);
		if (temp == NULL) {
			printf("error\n");
			return;
		}
		php->a = temp;
		php->capacity *= 2;
	}
	php->a[php->size] = x;
	php->size++;
	AdjustUp(php->a, php->size - 1);//减一是因为要与数组的下标相对应

}

7.堆的删除

堆的删除一般是删除对堆顶的元素进行删除，那么你是不是想的是，直接对下标为0的元素删除就好了。可是现实很骨感，这样做不能达到预期的效果，反而会让你的辈分升高。因为你直接删除之后，堆的结构就会混乱，也就会产生我原本是你兄弟，但是现在是你爸爸的结果，这可不辈分又升高了吗！

那么正确的删除步骤是什么呢？

step 1 ：先将堆顶元素与堆尾元素互换位置

step 2 ：删除堆尾元素

step 3：从堆顶开始，进行向下调整

向下调整算法：
前提：左右子树必须是堆

因为我们只是交换了堆顶元素和堆尾元素，那么其余元素的关系并没有改变，因此可以采用向下调整法。

下面具体介绍向下调整算法

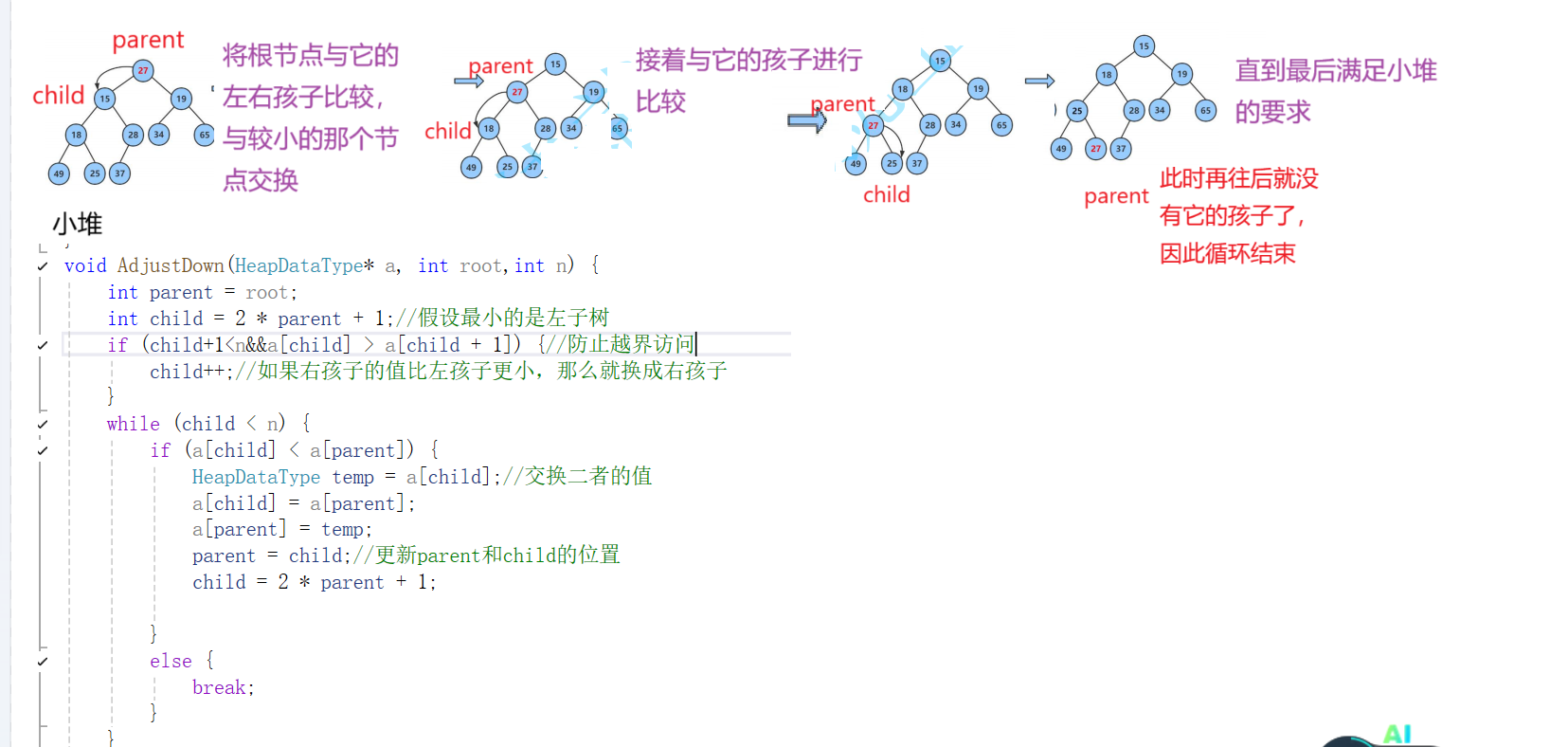
代码表达

void AdjustDown(HeapDataType* a, int root,int n) {
	int parent = root;
	int child = 2 * parent + 1;//假设最小的是左子树
	if (child+1<n&&a[child] > a[child + 1]) {//防止越界访问
		child++;//如果右孩子的值比左孩子更小，那么就换成右孩子
	}
	while (child < n) {
		if (a[child] < a[parent]) {
			HeapDataType temp = a[child];//交换二者的值
			a[child] = a[parent];
			a[parent] = temp;
			parent = child;//更新parent和child的位置
			child = 2 * parent + 1;

		}
		else {
			break;
		}
	}
}

准备工作完毕，正式开始堆的删除

void HeapPop(HP* php) {
	assert(php);
	assert(!HeapEmpty(php)); // 确保堆非空

	// 直接把最后一个元素覆盖堆顶，然后调整
	php->a[0] = php->a[php->size - 1];
	php->size--;
	AdjustDown(php->a, 0, php->size); // 从 root=0 开始调整
}

完整代码（这个代码只适用于小堆，但是大堆的逻辑是差不多的，可以自己尝试一下）

Heap.h
#pragma once
#include<assert.h>
#include<stdio.h>
#include<string.h>
#include<stdbool.h>
#include<stdlib.h>
typedef int HeapDataType;
typedef struct Heap{
	HeapDataType* a;
	int size;
	int capacity;

}HP;
void HeapInit(HP* heap);
void HeapDestory(HP* heap);
bool HeapEmpty(HP* heap);
int HeapSize(HP* heap);
HeapDataType HeapTop(HP* heap);
void AdjustUp(HeapDataType*a,int child);
void HeapPush(HP* heap,HeapDataType x);
void AdjustDown(HeapDataType* a, int root,int n);
void HeapPop(HP* heap);

Heap.c
#include"heap.h"
void HeapInit(HP* php) {
	assert(php);
	php->size = 0;
	php->capacity = 4;
	HeapDataType* a = (HeapDataType*)malloc(sizeof(HeapDataType)*4);
	if (a == NULL) {
		printf("error\n");
		return;
	}
	
	php->a = a;

}
void HeapDestory(HP* php) {
	assert(php);
	php->size = php->capacity = 0;
	free(php->a);
	php->a = NULL;
}
bool HeapEmpty(HP* php) {
	assert(php);
	return php->size == 0;
}
int HeapSize(HP* php) {
	assert(php);
	return php->size;
}
HeapDataType HeapTop(HP* php) {
	assert(php);
	return php->a[0];
}
void AdjustUp(HeapDataType* a, int child) {
	int parent = (child - 1) / 2;//这里运用了二叉树的性质哦，不记得的话可以往上翻翻
	while (child > 0) {
		if (a[child] < a[parent]) {
			HeapDataType temp = a[child];
			a[child] = a[parent];
			a[parent] = temp;
			child = parent;
			parent = (child - 1) / 2;
		}
		else {
			break;
		}
	}
}
void HeapPush(HP* php, HeapDataType x) {
	assert(php);
	//插入数据前我们还得判断数组是不是已经满了，如果满了，则需要扩容
	if (php->size == php->capacity) {
		HeapDataType* temp = (HeapDataType*)realloc(php->a, sizeof(HeapDataType) * php->capacity * 2);
		if (temp == NULL) {
			printf("error\n");
			return;
		}
		php->a = temp;
		php->capacity *= 2;
	}
	php->a[php->size] = x;
	php->size++;
	AdjustUp(php->a, php->size - 1);//减一是因为要与数组的下标相对应

}
void AdjustDown(HeapDataType* a, int root,int n) {
	int parent = root;
	int child = 2 * parent + 1;//假设最小的是左子树
	if (child+1<n&&a[child] > a[child + 1]) {//防止越界访问
		child++;//如果右孩子的值比左孩子更小，那么就换成右孩子
	}
	while (child < n) {
		if (a[child] < a[parent]) {
			HeapDataType temp = a[child];//交换二者的值
			a[child] = a[parent];
			a[parent] = temp;
			parent = child;//更新parent和child的位置
			child = 2 * parent + 1;

		}
		else {
			break;
		}
	}
}
void HeapPop(HP* php) {
	assert(php);
	assert(!HeapEmpty(php)); // 确保堆非空

	// 直接把最后一个元素覆盖堆顶，然后调整
	php->a[0] = php->a[php->size - 1];
	php->size--;
	AdjustDown(php->a, 0, php->size); // 从 root=0 开始调整
}