数据结构上课笔记（连载中...）-优快云博客

本文链接：https://blog.youkuaiyun.com/2401_87059016/article/details/146493564

二叉树

完全二叉树的两个性质：

1、具有n个节点的完全二叉数的深度为： $\left \lfloor log_{2}n \right \rfloor+1$

2、完全二叉树的节点编号与父子关系：对任意节点 i ，它的左孩子为 2*i , 右孩子为 2*i+1.

证明：用数学归纳法证明，i = 1时，其左孩子为 2；假设对任意节点 i ，它的左孩子为 2*i ，所以对于 i+1 的节点，因为其有左孩子，所以节点 i 有右孩子 2*i + 1,所以 i+1 的左节点作为其的后继，所以其左孩子的编号为 2*(i+1).

一颗完全二叉数上有1001个节点，其中叶子节点的个数为？

答案：501；

分析：先求最后的非叶子节点的编号，由最后的叶子节点编号1001，所以其父节点为最后的非叶子节点 $\left \lfloor 1001/2 \right \rfloor$ = 500；所以叶子节点个数为 1001 - 500 = 501 个。

二叉树的存储：

1、顺序存储

满二叉树或完全二叉数的顺序结构。用一组连续的内存单元，按编号顺序依次存储完全二叉树的元素。

非完全二叉树的形式补齐二叉树所缺少的那些结点，对二叉树结点编号，将二又树原有的结点按编号存储到内存单元“相应”的位置上。

由于一般二又树必须仿照完全二又树存储，可能会浪费很多存储空间，单支树就是一个极端情况

2、链式存储

二叉链表中每个结点包含三个域:数据域、左指针域、右指针域。

typedef struct node{
    int data;
    struct node *left_child;
    struct node *right_child;
}node,*BiTree;

若一个二叉树含有n个节点，则它的二叉链表中必含有2n个指针域，其中必有多少个空的链域？

答案：n+1;

分析：空链域 = 总指针域 - 边 = 2n - (n-1) = n+1;

三叉链表：为了便于找到双亲结点，可以增加一个Parent域，以指向该结点的双亲结点。三叉链表中每个结点包含四个域:数据域、双亲指针域、左指针域、右指针域

typedef struct node{
    int data;
    struct node *left_child;
    struct node *right_child;
    struct node *parent;
}node,*BiTree;

二叉树的遍历：

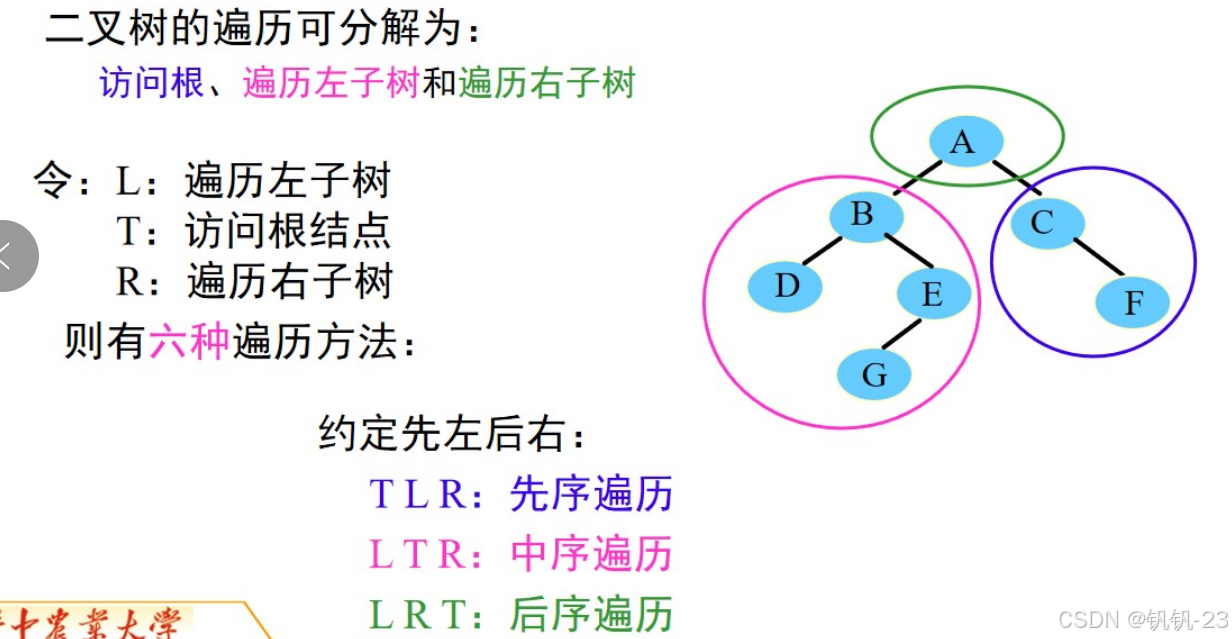
1、先序遍历

void TLR(BiTree root){
    if(root==NULL)return;
    cout << root->data << " ";
    TLR(root->left_child);
    TLR(root->right_child);
}

2、中序遍历

void LTR(BiTree root){
    if(root==NULL)return;
    LTR(root->left_child);
    cout << root->data << " ";
    LTR(root->right_child);
}

3、后序遍历

void LRT(BiTree root){
    if(root==NULL)return;
    LRT(root->left_child);
    LRT(root->right_child);
    cout << root->data << " ";
}

4、非递归遍历（用栈模拟先序，中序，后序遍历）

void stackRTL(BiTree root) {
    if (root == NULL) return;
    stack<BiTree> s;
    s.push(root);
    while (!s.empty()) {
        BiTree node = s.top();
        s.pop();
        cout << node->data << " ";
        
        if (node->right_child) s.push(node->right_child);
        if (node->left_child) s.push(node->left_child);
    }
}
void stackLTR(BiTree root){
    stack<BiTree>s;
    BiTree curr = root;
    while(curr != NULL || !s.empty()){
        while(curr != NULL){
            s.push(curr);
            curr = curr->left_child;
        }
        curr = s.top();
        s.pop();
        cout << curr->data << " ";

        curr = curr->right_child;
    }
}
void stackRTL(BiTree root){
    if(root == NULL)return;
    stack<BiTree>s1,s2;
    while(!s1.empty()){
        BiTree node  = s1.top();
        s1.pop();
        s2.push(node);

        if(node->left_child)s1.push(node->left_child);
        if(node->right_child)s2.push(node->right_child);
    }
    while(!s2.empty()){
        cout << s2.top()->data << " ";
        s2.pop();
    }
}

二叉数的创建

1、用前序遍历创建二叉树

void creatTree(Tree &root, string &s, int &index) {
    if (index >= s.length()) return;
    
    char c = s[index++];
    if (c == '.') {
        root = NULL;
    } else {
        root = new node{c, NULL, NULL};
        creatTree(root->left_child, s, index);
        creatTree(root->right_child, s, index);
    }
}

2、计算节点的个数

二叉树的结点个数等于左子树的结点数加上右子树的结点数再加上根结点数1，因此求二叉树的结点数的问题可以分解为计算其左右子树的结点数目问题

int nodecounthelp(Tree root) { // 修改1：添加返回值类型int
    if(root == NULL){
        return 0;
    }else{
        return 1 + nodecounthelp(root->left_child) + nodecounthelp(root->right_child); // 修改2：修正函数名拼写
    }
}

3、求二叉树的高度

int heighthelp(Tree root){
    if(root == NULL){
        return 0;
    }else{
        return 1+max(heighthelp(root->left_child),heighthelp(root->right_child));
    }
}

4、二叉树的销毁

void DestroyHelp(BinTreeNode* r) {
    if(r != NULL) {
        DestroyHelp(r->leftChild);
        DestroyHelp(r->rightChild);
        delete r;
    }
}

5、统计子节点的个数

int CountLeaves(BinTreeNode* root) {
    if(root == nullptr) return 0;
    if(root->leftChild == nullptr && root->rightChild == nullptr) return 1;
    return CountLeaves(root->leftChild) + CountLeaves(root->rightChild);
}

6、按树状打印二叉树

void DisplayBTWithTreeShapeHelp(Bin TreeNode*r,int level)
{
    if(r != NULL)
    {
        DisplayBTWithTreeShapeHelp(r->rightChild,level+1);
        for(int i = 0;i < level-1;i++){
            cout << " ";
        }
        cout << r->data;
        DisplayBTWithTreeShapeHelp(r->leftChild,level+1);
    }
}

7、二叉树的宽度

int MaxWidth(BinTreeNode* root) {
    if(root == nullptr) return 0;
    
    queue<BinTreeNode*> q;
    q.push(root);
    int max_width = 1;
    
    while(!q.empty()) {
        int level_size = q.size();
        max_width = max(max_width, level_size);
        
        for(int i = 0; i < level_size; i++) {
            BinTreeNode* node = q.front();
            q.pop();
            
            if(node->leftChild != nullptr) {
                q.push(node->leftChild);
            }
            if(node->rightChild != nullptr) {
                q.push(node->rightChild);
            }
        }
    }
    return max_width;
}

8、由二叉树的先序和中序序列建树

P1827 [USACO3.4] 美国血统 American Heritage - 洛谷https://www.luogu.com.cn/problem/P1827

#include <bits/stdc++.h>
#include <cstring>
using namespace std;
typedef struct Node{
    char date;
    struct Node * left;
    struct Node * right;
}Node,*Tree;

int get_place(string pre,char c){
    for(int i = 0;i < pre.size();i++){
        if(pre[i] == c){
            return i;
        }
    }
    return -1;
}
void F(string mid,string prv,string & left_mid,string & left_prv,string & right_mid,string & right_prv,int place){
    if (place > 0) {
        left_mid = mid.substr(0, place);
        left_prv = prv.substr(1, place);  // 仅当有左子树时分割
    }
    
    // 右子树分割
    if (place < mid.size()-1) {  // 添加右子树存在判断
        right_mid = mid.substr(place+1);
        // 添加保护防止越界
        if (prv.size() > place+1) {
            right_prv = prv.substr(place+1);
        }
    }
}
void solve(string mid,string prv,Tree & nownode){
    if(mid.empty()){
        nownode = NULL;
        return;
    }
    char c = prv[0];
    Tree newnode = new Node{c,NULL,NULL};
    nownode = newnode;
    if(mid.size() == 1){
        return;
    }
    int place = get_place(mid,c);
    string left_mid;
    string left_prv;
    string right_mid;
    string right_prv;
    F(mid,prv,left_mid,left_prv,right_mid,right_prv,place);
    solve(left_mid,left_prv,newnode->left);
    solve(right_mid,right_prv,newnode->right);
}

void ans(Tree & head){
    if(head == NULL){
        return;
    }
    ans(head->left);
    ans(head->right);
    cout << head->date;
}
int main(){
    string mid;
    string prv;
    cin >> mid;
    cin >> prv;
    Tree head = NULL;
    solve(mid,prv,head);

    ans(head);

    return 0;
}

线索二叉树

线索二叉树的出现是为了充分利用叶子节点的左右孩子的指针，所以可以让其指向（先序，中序，后序）遍历的前驱和后继。

所以我们需要增加两个标识符

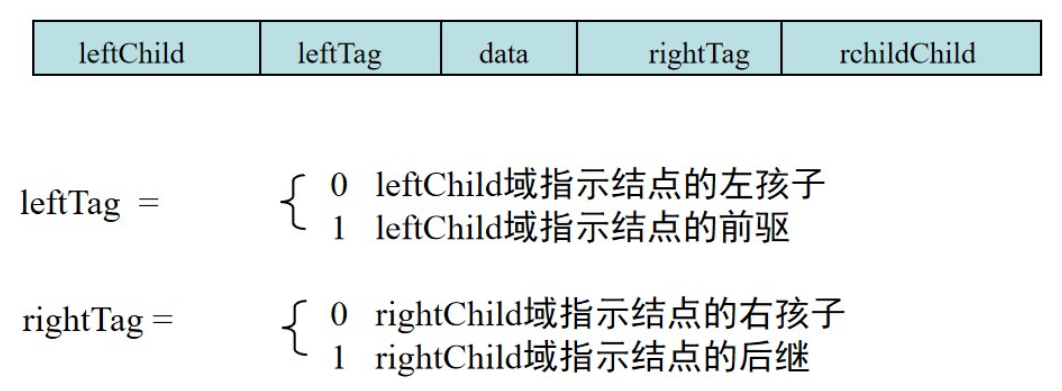
typedef struct Node{
    int data;
    Tree leftchild,rightchild;
    int lefttag,righttag;
}Node,*Tree;

线索二叉树（线索化）

以中序线索二叉树的线索化为例。

// 全局变量，用于线索化时记录前驱节点
Node *pre = nullptr;

// 中序线索化二叉树
void InThreading(Node *p) {
    if (p) {
        InThreading(p->leftchild); // 递归左子树线索化
        
        if (!p->leftchild) {       // 左孩子为空，建立前驱线索
            p->lefttag = 1;
            p->leftchild = pre;
        } else {
            p->lefttag = 0;
        }
        
        if (pre && !pre->rightchild) { // 前驱节点的右孩子为空，建立后继线索
            pre->righttag = 1;
            pre->rightchild = p;
        }
        
        pre = p; // 保持pre指向p的前驱
        
        InThreading(p->rightchild); // 递归右子树线索化
    }
}

线索二叉树的遍历

1、中序线索二叉树的遍历

void InOrderTraverse_Thr(Tree T) {
    Node *p = T;
    while (p) {
        // 1. 找到最左下的节点（中序遍历起点）
        while (p->lefttag == 0) {
            p = p->leftchild;
        }
        
        // 2. 访问当前节点
        cout << p->data << " ";
        
        // 3. 如果右指针是线索，直接访问后继
        while (p->righttag == 1) {
            p = p->rightchild;
            cout << p->data << " ";
        }
        
        // 4. 否则转向右子树
        p = p->rightchild;
    }
}

2、中序线索二叉树求后继节点

Node* InOrderSuccessor(Node* p) {
    if (p == nullptr) return nullptr;
    
    // 如果右标记是线索，直接返回右孩子（即后继）
    if (p->righttag == 1) {
        return p->rightchild;
    }
    // 否则，后继是右子树的最左下节点
    else {
        Node* temp = p->rightchild;
        while (temp && temp->lefttag == 0) {
            temp = temp->leftchild;
        }
        return temp;
    }
}

3、中序线索二叉树求前驱节点

Node* InOrderPredecessor(Node* p) {
    if (p == nullptr) return nullptr;
    
    // 如果左标记是线索，直接返回左孩子（即前驱）
    if (p->lefttag == 1) {
        return p->leftchild;
    }
    // 否则，前驱是左子树的最右下节点
    else {
        Node* temp = p->leftchild;
        while (temp && temp->righttag == 0) {
            temp = temp->rightchild;
        }
        return temp;
    }
}

线索二叉树的节点插入与删除

1、在中序线索二叉树中插入节点

1、新的节点插入到二叉树中，作为某节点的左孩子：

2、新的节点插入到二叉树中，作为某节点的右孩子：

// 在节点p的右子树插入新节点newNode
void InsertRightChild(Node* p, Node* newNode) {
    if (p == nullptr || newNode == nullptr) return;
    
    // 保存p原来的右子树
    Node* oldRight = p->rightchild;
    
    // 设置新节点的左右指针
    newNode->leftchild = p;       // 新节点的前驱是p
    newNode->lefttag = 1;         // 设置为线索
    newNode->rightchild = oldRight; // 新节点的后继是p原来的后继
    newNode->righttag = p->righttag;
    
    // 更新p的右孩子为新节点
    p->rightchild = newNode;
    p->righttag = 0;  // 设置为普通孩子指针
    
    // 如果p原来有右孩子(不是线索)
    if (oldRight != nullptr && newNode->righttag == 0) {
        // 找到oldRight的最左下节点(中序第一个节点)
        Node* temp = oldRight;
        while (temp->lefttag == 0) {
            temp = temp->leftchild;
        }
        // 更新oldRight的前驱线索
        temp->leftchild = newNode;
    }
}

2、在中序线索二叉树中删除节点

树

树的存储结构

1、双亲表示法

采用一组连续的空间存储树的节点，通过存储每个节点的双亲位置，表示节点之间的结构关系。

// 1、双亲表示法
typedef struct ParentTreeNode{
    int data;
    int parent;
}ParentTreeNode;
typedef struct Tree{
    ParentTreeNode arr[50];
    int nodenum;
}Tree;

2、孩子表示法

把每个节点的孩子节点排列在一起，看成一个线性表

// 2、孩子表示法（邻接表形式）
typedef struct ChildNode {   // 孩子节点
    int index;               // 孩子下标
    struct ChildNode* next;  // 指向下一个孩子
} ChildNode;

typedef struct {
    int data;                // 节点数据
    ChildNode* firstChild;   // 第一个孩子指针
} TreeNode;

typedef struct {
    TreeNode nodes[50];      // 节点数组
    int root;                // 根节点位置
    int nodeNum;             // 节点总数
} ChildTree;

3、孩子兄弟表示法（二叉树表示法）

用二叉链表作为树的存储结构。链表的两个指针域分别指向该节点的第一个孩子节点和下一个兄弟节点


// 3、孩子兄弟表示法（二叉树表示法）
typedef struct CSNode {
    int data;
    struct CSNode* firstChild;  // 第一个孩子指针
    struct CSNode* nextSibling; // 右兄弟指针
} CSNode, *CSTree;

二叉树表示法转化为孩子表示法

// ... 原有结构体定义保持不变 ...

// 递归转换辅助函数
static int convertNode(CSTree node, int parentIdx, ChildTree* ct) {
    int currentIdx = ct->nodeNum++;
    ct->nodes[currentIdx].data = node->data;
    ct->nodes[currentIdx].firstChild = nullptr;

    // 将当前节点添加到父节点的孩子链表
    if (parentIdx != -1) {
        ChildNode* newChild = new ChildNode{currentIdx, ct->nodes[parentIdx].firstChild};
        ct->nodes[parentIdx].firstChild = newChild;
    }

    // 递归处理第一个孩子
    if (node->firstChild) {
        convertNode(node->firstChild, currentIdx, ct);
    }

    // 递归处理右兄弟
    if (node->nextSibling) {
        convertNode(node->nextSibling, parentIdx, ct);
    }

    return currentIdx;
}

void CSTreeToChildTree(CSTree cs, ChildTree* ct) {
    ct->nodeNum = 0;
    ct->root = -1;
    if (!cs) return;
    
    ct->root = convertNode(cs, -1, ct);
}

森林和二叉树的转换

可以做一个虚拟根（在二叉树中不表示，只是方便理解）连接所以树的根节点。

树与森林的遍历

先根遍历

        -若树非空，则遍历方法为：

        -1、访问根节点

        -2、从左到右，依次先根遍历根节点的每一颗子树

后根遍历

-若树非空，则遍历方法为：

-1、从左到右，依次后根遍历根节点的每一颗子树

-2、访问根节点

哈夫曼树（huffmam）

基本概念

路径：从一个节点到另一个节点之间的若干个分支；

路径长度：路径上的分支数目称路径长度；

节点的路径长度：从根到该节点的路径长度；

树的路径长度：树中所有节点的路径长度之和；一般记为PL;

在节点数相同的条件下，完全二叉树是路径最短的二叉树。

节点的权：根据应用需要可以给树的节点赋权值；

节点的带权路径长度：从根到该节点的路径长度与该节点权的乘积；

树的带权路径长度=树中所有叶子节点的带权路径之和，常记作：WPL.

在求得某些判定问题时，利用哈夫曼树获得最佳判定算法。

程序结构的不同，导致比较的次数不同，所以我们应该如何设计程序来减小程序比较的次数？

可以通过哈夫曼树来解决问题。

哈夫曼树的构造

        - 根据给定的n个权值，构造n棵只有一个根结点的二叉树，n个权值分别是这些二叉树根结点的权。设F是由这n棵二叉树构成的集合。

        - 在F中选取两棵根结点树值最小的树作为左、右子树，构造一棵新的二叉树，置新二叉树根的权值=左、右子树根结点权值之和；

        - 从F中删除这两颗树，并将新树加入F；

        - 重复2、3，直到F中只含一棵树为止；

#include <bits/stdc++.h>
using namespace std;
typedef struct Node{
    int data;
    int left,right;
    // 小的为left,大的为right
    int8_t parent;
}Node;
int main(){
    int n;cin >> n;
    vector<Node>arr(2*n);
    priority_queue<int,vector<int>,greater<int>>pq;
    for(int i = 1;i <= n;i++){
        int temp;cin >> temp;
        arr[i].data = temp;
        arr[i].left = arr[i].right = arr[i].parent = 0;
        pq.push(temp);
    }
    for(int i = n+1;i <= 2*n-1;i++){
        int a = pq.top();pq.pop();int a_place = 0;
        for(int j = 1;j < i;j++){
            if(arr[j].data == a){
                a_place = j;
            }
        }
        int b = pq.top();pq.pop();int b_place = 0;
        for(int j = 1;j < i;j++){
            if(arr[j].data == b){
                b_place = j;
            }
        }
        int c = a+b;pq.push(c);
        arr[i].data = c;
        arr[i].left = a_place;
        arr[i].right = b_place;
        arr[a_place].parent = i;
        arr[b_place].parent = i;
    }
    return 0;
}

哈夫曼树的应用

哈夫曼编码

前缀码：如果在任何一个编码系统中，任何一个编码都不是其他编码的前缀，则称该编码系统中的编码是前缀码。

我们可以通过哈夫曼树来设计各个编码与前缀码的对应关系

【问题描述】读入n个字符所对应的权值，自底向上构造一棵哈夫曼树，自顶向下生成每一个字符对应的哈夫曼编码，并依次输出。另，求解某字符串的哈夫曼编码，求解某01序列的译码。

【输入形式】输入的第一行包含一个正整数n，表示共有n个字符需要编码。其中n不超过100。第二行中有n个用空格隔开的正整数，分别表示n个字符的权值，依次按照abcd...的默认顺序给出。然后是某字符串和某01序列。

【输出形式】前n行，每行一个字符串，表示对应字符的哈夫曼编码。然后是某字符串的哈夫曼编码，某01序列的译码。

【注意】保证每次左子树比右子树的权值小；如出现相同权值的，则先出现的在左子树，即下标小的在左子树。

【样例输入】

8
5 29 7 8 14 23 3 11

aabchg

00011110111111001

【样例输出】

0001
10
1110
1111
110
01
0000
001

000100011011100010000

acdef

#include <bits/stdc++.h>
using namespace std;
typedef struct Node{
    char c;
    int data;
    int left,right;
    // 小的为left,大的为right
    int parent;
    string str;
}Node;
string F(int place, vector<Node>& arr) {
    if (arr[place].parent == 0) return "";
    if (arr[arr[place].parent].left == place) {
        return F(arr[place].parent, arr)+"0";
    } else {
        return F(arr[place].parent, arr)+"1";
    }
}

int main(){
    int n;cin >> n;
    vector<Node>arr(2*n);
    priority_queue<int,vector<int>,greater<int>>pq;
    for(int i = 1;i <= n;i++){
        int temp;cin >> temp;
        arr[i].data = temp;
        arr[i].left = arr[i].right = arr[i].parent = 0;arr[i].c = 'a'+i-1;
        pq.push(temp);
    }
    string s;cin >> s;
    string t;cin >> t;
    for(int i = n+1;i <= 2*n-1;i++){
        
        int a = pq.top();pq.pop();int a_place = 0;
        for(int j = 1;j < i;j++){
            if(arr[j].data == a && arr[j].parent == 0){  
                a_place = j;
                break; 
            }
        }
        
        int b = pq.top();pq.pop();int b_place = 0;
        for(int j = 1;j < i;j++){
            if(arr[j].data == b && arr[j].parent == 0 && j != a_place){  
                b_place = j;
                break;
            }
        }
        int c = a+b;pq.push(c);
        arr[i].data = c;
        arr[i].left = a_place;
        arr[i].right = b_place;
        arr[a_place].parent = i;
        arr[b_place].parent = i;
    }
    
    
    for(int i = 1;i <= n;i++){
        string code = F(i,arr);
        arr[i].str = code;
        cout << code << '\n';
    }

    for(int i = 0;i < s.size();i++){
        cout << arr[s[i]-'a'+1].str;
    }
    cout << '\n';
    int nowplace = 2*n-1;
    for(int i = 0;i < t.size();i++){
        if(t[i]=='1'){
            nowplace = arr[nowplace].right;
        }else{
            nowplace = arr[nowplace].left;
        }
        if(arr[nowplace].left==0&&arr[nowplace].right==0){
            cout << arr[nowplace].c;
            nowplace = 2*n-1;
        }
    }
    return 0;
}

图

图的定义与基础术语

定义：图是由顶点集合与边的集合组成的一种数据结构；

完全图：

        1、无向完全图：有n(n-1)/2条边（图中的每个顶点和其余的n-1个顶点都有边相连）的无向图为无向完全图。

        2、有向完全图：有n(n-1)条边（图中的每个顶点和其余的n-1个顶点都有弧相连）的有向图为有向完全图。

联通图（强连通图）：

        在无（有）向图G中，若任何两个顶点v,u有存在v到u的路径，则称G是联通图（强连通图）。

联通分量（强联通分量）：

无向图G的极大联通子图称为G的联通分量

极大联通子图：

将G的任何不在该子图中的顶点加入，子图不再联通。

生成树：

包含无向图G所有顶点的极小联通子图称为G的生成树。若T是G的生成树当前仅当T满足以下条件：1、T是G的联通子图；2、T包含G的所有顶点；3、T中无回路

图的存储结构

邻接矩阵表示法

无向图的邻接矩阵为对称矩阵，有向图不是。对于带权重的图可以用将权重填入邻接表中表示带权重的图。

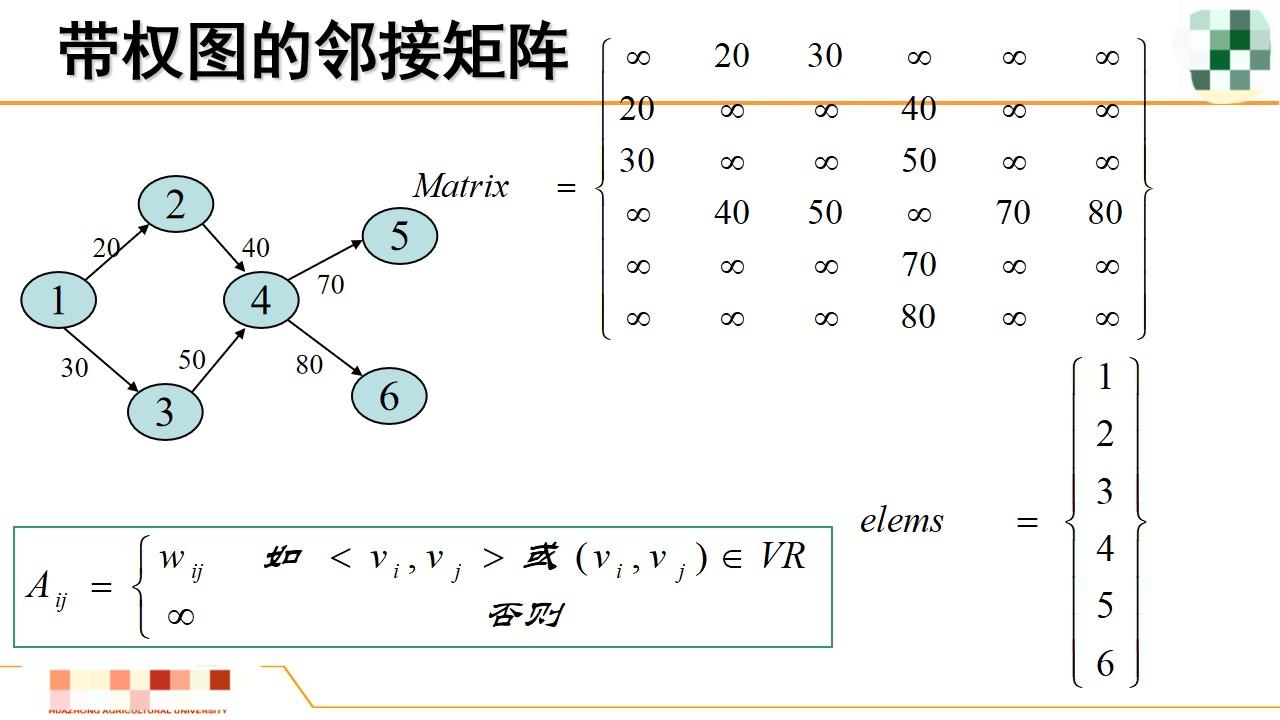
#define MAX_VERTEX_NUM 20  // 最大顶点数

// 图的邻接矩阵存储结构
struct Graph {
    int v;                      // 顶点数
    int e;                      // 边数
    char vexs[MAX_VERTEX_NUM];  // 顶点表
    int matrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; // 邻接矩阵
};

邻接表

#define MAX_VERTEX_NUM 20  // 最大顶点数

class Grape{
private:
    int v;   // 顶点数
    int e;   // 边数
    vector<char>vexs;
    vector<int>adj[MAX_VERTEX_NUM];
};

逆邻接表（为了方便求入度）

与邻接表的代码一样，但是 vector<int>adj 的意义不同；

#define MAX_VERTEX_NUM 20  // 最大顶点数

class Grape{
private:
    int v;   // 顶点数
    int e;   // 边数
    vector<char>vexs;
    vector<int>adj[MAX_VERTEX_NUM];
};

图的遍历

深度优先搜索(DFS)

DFS（函数递归版）模版：

void dfs(int step){
    if(达到目的地){
        输出解
        返回
    }
    合理的剪枝操作
    for(int i = 1;i <= 枚举数;i++){
        if(满足条件){
            更新状态位
            dfs(step+1)
            恢复状态位
        }
    }
}

非递归进行DFS：

#include <bits/stdc++.h>
using namespace std;
const int N = 8;
vector<int>g[N+1];
vector<bool>visited(N+1,false);
int main(){
    for(int i = 0;i < 9;i++){
        int u,v;
        cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    stack<int>st;
    st.push(1);
    while(!st.empty()){
        int v = st.top();
        if(!visited[v]){
            cout << v << ' ';
            visited[v]=true;
        }
        int w = -1;
        for(int i : g[v]){
            if(visited[i]==false){
                w = i;
                break;
            }
        }
        if(w != -1){
            st.push(w);
        }else{
            st.pop();
        }
    }
    return 0;
}

例题：

P1219 [USACO1.5] 八皇后 Checker Challengehttps://www.luogu.com.cn/problem/P1219

广度优先搜索(BFS)

#include <bits/stdc++.h>
using namespace std;
const int N = 8;
vector<int>g[N+1];
vector<bool>visited(N+1,false);
int main(){
    for(int i = 0;i < 9;i++){
        int u,v;
        cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    queue<int>q;
    q.push(1);
    while(!q.empty()){
        int a = q.front();
        q.pop();
        if(visited[a]==false){
            cout << a << ' ';
            visited[a] = true;
        }
        for(int i : g[a]){
            if(visited[i]==false){
                q.push(i);
            }
        }
    }
    return 0;
}

例题：

P5318 【深基18.例3】查找文献 - 洛谷https://www.luogu.com.cn/problem/P5318

图的连通性问题

最小生成树问题

1、Prim 算法

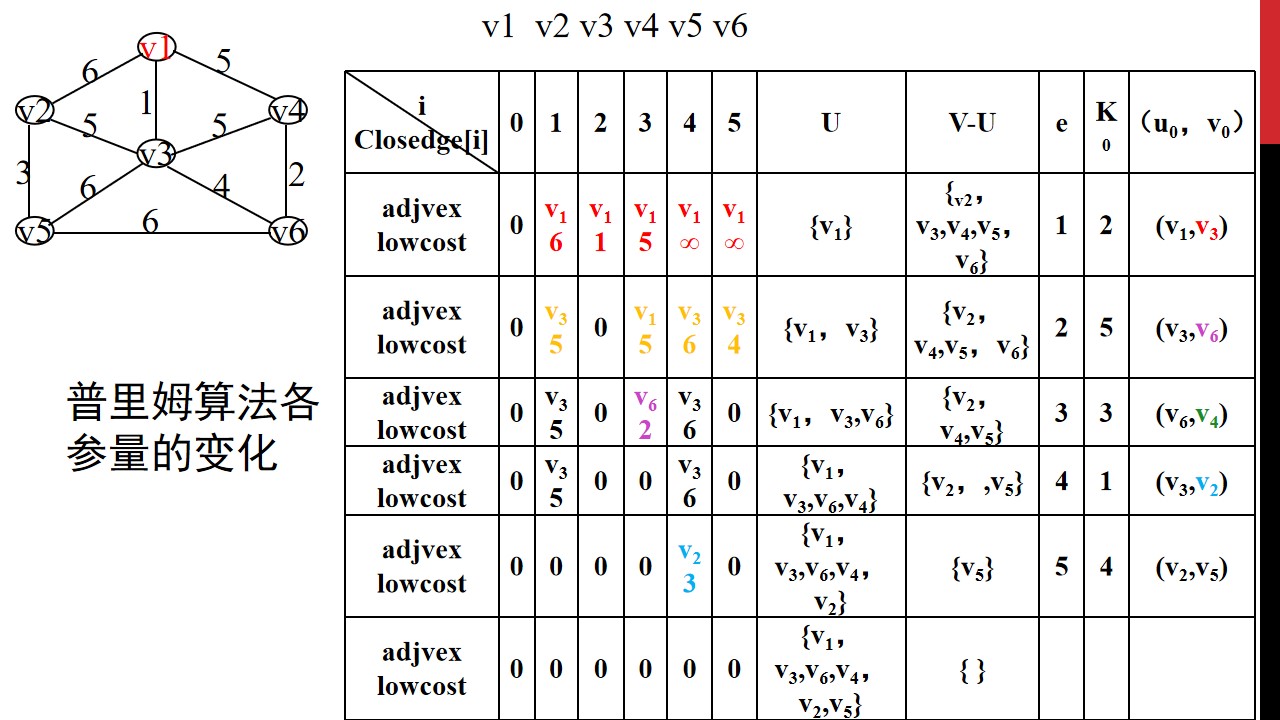
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5;
typedef pair<int,int> pii;
// 修改邻接表存储结构：pair<相邻节点, 边权>
vector<pair<int, int>> g[N+1]; 
vector<bool> vis(N+1, false); // 新增访问标记数组

int main(){
    int n, m;
    cin >> n >> m;
    
    // 构建邻接表
    for(int i = 0; i < m; i++){
        int u, v, w;
        cin >> u >> v >> w;
        g[u].emplace_back(v, w); // 无向图双向存储
        g[v].emplace_back(u, w);
    }

    // Prim算法核心实现
    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;
    int mst = 0;
    
    pq.push({0, 1}); // 从节点1开始（可根据题目要求调整）
    while(!pq.empty()){
        pii a = pq.top();
        int cost = a.first;
        int u = a.second;

        pq.pop();
        
        if(vis[u]) continue;
        vis[u] = true;
        mst += cost;
        
        for(auto i : g[u]){
            int v = i.first;
            int w = i.second;
            if(!vis[v]){
                pq.push({w, v});
            }
        }
    }
    
    cout << mst << endl;
    return 0;
}

2、Kruskal 算法

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5;
typedef struct edge{
    int u,v;
    int dit;
}edge;
bool cmp(edge a,edge b){
    return a.dit > b.dit;
}

int Find(int num,vector<int>&find){
    if(num == find[num]){
        return num;
    }else{
        return find[num] = Find(num,find);
    }
}
int main(){
    int n, m;
    cin >> n >> m;

    vector<int>g[n+1];
    vector<edge>edges(n+1);
    vector<int>find(n+1);
    vector<bool>visited(n+1,false);
    set<int>have_visited;
    
    for(int i = 0;i <= n;i++){
        find[i] = i;
    }

    for(int i = 0; i < m; i++){
        int u, v, w;
        cin >> u >> v >> w;
        g[u].push_back(v);
        g[v].push_back(u);
        edges.push_back({u,v,w});
    }

    int mst = 0;

    sort(edges.begin(),edges.end(),cmp);

    for(int i = 0;i < m;i++){
        edge e = edges[i];
        int u = e.u;
        int v = e.v;
        if(Find(u,find)==Find(v,find))continue;
        find[u]=v;
        mst+=e.dit;
        have_visited.insert(u);
        have_visited.insert(v);
        if(have_visited.size()==n){
            break;
        }
    }

    cout << mst << endl;
    return 0;
}

例题：P3366 【模板】最小生成树https://www.luogu.com.cn/problem/P3366 P1194 买礼物https://www.luogu.com.cn/problem/P1194

有向无环图的应用

拓扑排序

void topologicalSort(vector<vector<int>>& graph, int vertices) {
    vector<int> inDegree(vertices, 0);
    queue<int> q;
    // 计算每个顶点的入度
    for(int i = 0; i < vertices; i++) {
        for(int neighbor : graph[i]) {
            inDegree[neighbor]++;
        }
    }
    // 将所有入度为0的顶点加入队列
    for(int i = 0; i < vertices; i++) {
        if(inDegree[i] == 0) {
            q.push(i);
        }
    }
    int count = 0;
    vector<int> topOrder;
    while(!q.empty()) {
        int u = q.front();
        q.pop();
        topOrder.push_back(u);
        // 减少相邻顶点的入度
        for(int neighbor : graph[u]) {
            if(--inDegree[neighbor] == 0) {
                q.push(neighbor);
            }
        }
        count++;
    }
    // 检查是否有环
    if(count != vertices) {
        cout << "图中存在环，无法进行拓扑排序" << endl;
        return;
    }
    // 输出拓扑排序结果
    for(int i : topOrder) {
        cout << i << " ";
    }
    cout << endl;
}

例题：

B3644 【模板】拓扑排序 / 家谱树 - 洛谷https://www.luogu.com.cn/problem/B3644

#include <bits/stdc++.h>
using namespace std;
int n;
vector<vector<int>>arr;
int to[101];
int main(){
    cin >> n;
    for(int i = 0;i <= n;i++){
        vector<int>temp;
        arr.push_back(temp);
    }
    for(int i = 1;i <= n;i++){
        while(true){
            int num;
            cin >> num;
            if(num == 0){
                break;
            }else{
                arr[i].push_back(num);
                to[num]++;
            }
        }
    }
    queue<int>q;
    for(int i = 1;i <= n;i++){
        if(to[i] == 0){
            q.push(i);
        }
    }
    while(!q.empty()){
        int a = q.front();
        q.pop();
        cout << a << ' ';
        to[a]--;
        for(int i = 0;i < arr[a].size();i++){
            to[arr[a][i]]--;
            if(to[arr[a][i]] == 0){
                q.push(arr[a][i]);
            }
        }
    }
    return 0;
}

AOE(Activity On Edge)网络的关键路径分析

最短路径

Dijkstra算法

Dijkstra算法是一种用于解决单源最短路径问题的经典算法，由荷兰计算机科学家Edsger W. Dijkstra于1956年提出。该算法主要用于计算从起点到图中所有其他顶点的最短路径。

以下是Dijkstra算法的基本步骤：

初始化：将起点到自身的距离设置为0，将其余节点到起点的距离设置为无穷大。
选择距离起点最近的未访问节点作为当前节点。
根据当前节点更新与其相邻节点的距禮：对于每一个相邻节点，如果通过当前节点到该节点的距离小于当前记录的最短距离，则更新最短距离。
将当前节点标记为已访问。
重复步骤2至4，直到所有节点都被标记为已访问或者没有可以访问的节点。
根据记录的最短距离，得到起点到每个节点的最短路径。

Dijkstra算法通常使用优先级队列来实现，以提高搜索效率。这样在每一步选择最短路径节点时，可以快速找到距离起点最近的未访问节点。

总的来说，Dijkstra算法是一种贪婪算法，通过每次选择当前最优解来逐步构建最短路径。该算法保证了在图中没有负权边的情况下，能够找到从起点到其他所有节点的最短路径。

例题：

P4779 【模板】单源最短路径（标准版） - 洛谷https://www.luogu.com.cn/problem/P4779

#include <iostream>
#include <vector>
#include <queue>
#define int long long
using namespace std;

int n,m,s;
struct edge{
    int v,w;
};
struct node{
    int dis,u;
    bool operator > (const node & a)const{
        return  dis > a.dis;
    }
};

vector<edge>e[100005];
int dis[100005],vis[100005];
priority_queue<node,vector<node>,greater<node>>q;

void dijkstra(int n,int s){
    // memset(dis,0x3f3f3f3f3f,(n+1)*sizeof(int));
    // memset(vis,0,(n+1)*sizeof(int));
    for(int i = 0;i <= n;i++){
        dis[i] = 0x3f3f3f3f3f;
        vis[i] = 0;
    }
    dis[s] = 0;
    q.push({0,s});
    while(!q.empty()){
        int u = q.top().u;
        q.pop();
        if(vis[u])continue;
        vis[u] = 1;
        for(auto ed : e[u]){
            int v = ed.v,w = ed.w;
            if(dis[v] > dis[u]+w){
                dis[v] = dis[u] + w;
                q.push({dis[v],v});
            }
        }
    }
}
signed main(){
    cin >> n >> m >> s;
    for(int i = 0;i < m;i++){
        int u,v,dis;
        cin >> u >> v >> dis;
        e[u].push_back({v,dis});
    }
    dijkstra(n,s);
    for(int i = 1;i <= n;i++){
        cout << dis[i] << ' ';
    }
    return 0;
}

Floyd算法

Floyd算法，也称为Floyd-Warshall算法，是一种用于求解图中所有节点之间最短路径的动态规划算法。它采用一个二维数组来存储任意两点之间的最短距离，通过对这个数组的不断更新，最终得到所有节点之间的最短路径。

具体步骤如下：

初始化一个二维数组，用于存储任意两点之间的最短距离。将这个数组初始化为图中节点之间的直接距离，若两点之间没有直接相连，则距离设置为无穷大。
通过三重循环，对数组进行不断更新，更新规则为：若存在一个节点k，使得从节点i经过节点k再到节点j的路径距离更短，则更新节点i到节点j的最短距离为节点i到节点k再到节点j的距离。
最终得到的二维数组即为所有节点之间的最短路径。

Floyd算法的时间复杂度为O(n^3)，适用于有向图或无向图，可以处理有负权边但不能处理有负权环的情况。

例题：

B3647 【模板】Floyd - 洛谷https://www.luogu.com.cn/problem/B3647

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1001;
vector<vector<int>>ans(MAXN,vector<int>(MAXN,0x3f3f3f3f));
int main(){
    int n,m;
    cin >> n >> m;
    for(int i = 0;i< m;i++){
        int u,v,w;
        cin >> u >> v >> w;
        ans[u][v] = min(ans[u][v],w);
        ans[v][u] = min(ans[v][u],w);
    }
    for(int i = 1;i <= n;i++){
        ans[i][i] = 0;
    }
    for(int k = 1;k <= n;k++){
        for(int i = 1;i <= n;i++){
            for(int j = 1;j <= n;j++){
                ans[i][j] = min(ans[i][j],ans[i][k]+ans[k][j]);
            }
        }
    }
    for(int i = 1;i <= n;i++){
        for(int j = 1;j <= n;j++){
            cout << ans[i][j] << ' ';
        }
        cout << '\n';
    }
    return 0;
}

查找

基于树的查找

二叉排序树

二叉排序树（Binary Search Tree，BST）是一种特殊的二叉树，其中每个节点包含一个键值，并且满足以下性质：

左子树中所有节点的键值小于父节点的键值。
右子树中所有节点的键值大于父节点的键值。
左子树和右子树也都是二叉排序树。

由于这种特性，二叉排序树可以支持快速的搜索、插入和删除操作。通过保持树的有序性，可以在平均情况下实现对数时间复杂度的这些操作。

在实际应用中，二叉排序树常用于实现动态集合的数据结构，例如实现集合的查找、插入、删除等操作。但需要注意的是，如果二叉排序树的形态较为倾斜，可能会使得其性能下降至线性级别。

二叉排序树的创建

#include <iostream>
using namespace std;

struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;

    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

void insert(TreeNode* &root, int val) {
    if (root == nullptr) {
        root = new TreeNode(val);
        return;
    }

    if (val < root->val) {
        insert(root->left, val);
    } else {
        insert(root->right, val);
    }
}

void inorderTraversal(TreeNode* root) {
    if (root != nullptr) {
        inorderTraversal(root->left);
        cout << root->val << " ";
        inorderTraversal(root->right);
    }
}

int main() {
    TreeNode* root = nullptr;

    insert(root, 5);
    insert(root, 3);
    insert(root, 7);
    insert(root, 1);
    insert(root, 4);

    cout << "Inorder traversal of the binary search tree: ";
    inorderTraversal(root);
    cout << endl;

    return 0;
}

二叉排序树的查找

二叉排序树（BST）是一种特殊的二叉树，其每个节点包含一个值，且对于任意一个节点，其左子树上所有节点的值小于该节点的值，右子树上所有节点的值大于该节点的值。在二叉排序树中进行查找操作时，我们可以利用其特定的性质来快速定位目标值。

具体的查找过程如下：

从根节点开始，比较目标值与当前节点的值：
- 如果目标值等于当前节点的值，则直接返回当前节点，表示找到了目标值。
- 如果目标值小于当前节点的值，则在当前节点的左子树中继续查找。
- 如果目标值大于当前节点的值，则在当前节点的右子树中继续查找。
重复上述过程，直到找到目标值或者遇到空节点（表示未找到目标值）为止。

由于二叉排序树的性质，每次查找都可以根据目标值与当前节点值的大小关系，通过比较选择向左子树或右子树移动，可以在较快地时间内定位到目标值，最坏情况下的时间复杂度为 O(h)，其中 h 为树的高度。

需要注意的是，二叉排序树的查找算法仅适用于已经建立好的二叉排序树。在插入、删除节点时，需要保持二叉排序树的性质，以确保查找算法的正确性和效率。

#include <iostream>
using namespace std;

struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;

    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

TreeNode* search(TreeNode* root, int val) {
    if (root == nullptr || root->val == val) {
        return root;
    }

    if (val < root->val) {
        return search(root->left, val);
    } else {
        return search(root->right, val);
    }
}

int main() {
    TreeNode* root = nullptr;

    root = new TreeNode(5);
    root->left = new TreeNode(3);
    root->right = new TreeNode(7);
    root->left->left = new TreeNode(1);
    root->left->right = new TreeNode(4);

    cout << "Enter a value to search: ";
    int target;
    cin >> target;

    TreeNode* result = search(root, target);
    if (result != nullptr) {
        cout << "Value " << target << " is found in the binary search tree." << endl;
    } else {
        cout << "Value " << target << " is not found in the binary search tree." << endl;
    }

    return 0;
}

二叉排序树的删除

二叉排序树的删除操作相对复杂，需要考虑节点的不同情况。删除一个节点后，需要保持二叉排序树的性质不变。

具体的删除操作可以分为以下几种情况：

删除的节点是叶子节点（没有子节点）：直接删除该节点，将其父节点指向它的指针置为NULL。
删除的节点只有一个子节点：将父节点指向被删除节点的指针指向删除节点的子节点。
删除的节点有两个子节点：找到删除节点的中序遍历的前驱或后继节点来替换删除节点。中序遍历的前驱节点是小于删除节点值的最大节点，即删除节点左子树的最右节点；中序遍历的后继节点是大于删除节点值的最小节点，即删除节点右子树的最左节点。用这个前驱或后继节点替换删除节点，再删除前驱或后继节点。

下面是一个简单的示例代码，实现二叉排序树的删除操作：

struct Node {
    int value;
    Node* left;
    Node* right;
};

Node* findMin(Node* node) {
    while (node->left != NULL) {
        node = node->left;
    }
    return node;
}

Node* deleteNode(Node* root, int key) {
    if (root == NULL) {
        return root;
    }
    
    if (key < root->value) {
        root->left = deleteNode(root->left, key);
    } else if (key > root->value) {
        root->right = deleteNode(root->right, key);
    } else {
        if (root->left == NULL) {
            Node* temp = root->right;
            delete root;
            return temp;
        } else if (root->right == NULL) {
            Node* temp = root->left;
            delete root;
            return temp;
        }
        
        Node* temp = findMin(root->right);
        root->value = temp->value;
        root->right = deleteNode(root->right, temp->value);
    }
    return root;
}

在代码中，函数 deleteNode 实现了二叉排序树的节点删除操作，根据不同情况选择合适的操作。需要注意，在实际应用中可能还需要考虑更多情况和细节，例如内存释放等。

二叉排序树的查找性能

平衡二叉排序树

平衡二叉排序树（Balanced Binary Search Tree）是一种特殊的二叉排序树，其左子树和右子树的高度差不超过 1，从而保持树的平衡性。平衡二叉排序树的平衡性可以确保在最坏情况下，搜索、插入和删除等操作的时间复杂度能够保持在较低水平，通常为 O(log n)。

常见的平衡二叉排序树包括：

AVL 树：最早被发明的平衡二叉搜索树，保证了树的高度相对较低，从而保持了较好的性能。
红黑树（Red-Black Tree）：一种自平衡的二叉搜索树，通过一系列旋转和颜色变换操作来维持树的平衡。
Splay 树：一种自适应的平衡树，通过旋转和伸展操作来调整节点位置，使得经常访问的节点会被调整到根节点位置，提高了访问性能。

这些平衡二叉排序树的设计旨在保持树的平衡，从而确保树的高度不会过高，提高搜索效率，适用于大部分需要频繁搜索、插入、删除操作的应用场景。

AVL 树的构造

AVL 树是一种自平衡的二叉搜索树，它通过保持每个节点的平衡因子（Balance Factor）来确保树的平衡。平衡因子是指某个节点的左子树高度减去右子树高度的值，即 Balance Factor = Height(left) - Height(right)。在 AVL 树中，每个节点的平衡因子只能是 -1、0 或 1。

AVL 树的构造过程包括插入和删除节点时的旋转操作，以恢复树的平衡。具体构造过程如下：

插入节点：当向 AVL 树中插入新节点时，首先按照二叉搜索树的规则找到插入位置，将新节点插入到合适的位置。然后，从插入节点到根节点的路径上，检查每个祖先节点的平衡因子，如果出现了平衡因子不为 -1、0 或 1 的情况，说明树失去了平衡，需要通过旋转操作来恢复平衡。平衡维护的具体方法通常有四种：左旋、右旋、左右旋和右左旋。
删除节点：当从 AVL 树中删除节点时，首先按照二叉搜索树的规则找到要删除的节点。删除节点后，同样需要从删除节点到根节点的路径上检查每个祖先节点的平衡因子，如果平衡因子不符合要求，需要进行旋转操作来重新平衡 AVL 树。

通过以上的插入和删除操作并配合旋转操作，AVL 树能够保持每个节点的平衡因子在 -1、0 或 1，从而确保树的平衡。总的来说，AVL 树的构造过程是一个不断调整平衡因子并进行旋转操作的过程，以维持树的平衡性。

LL情况：（新插入结点在危机结点的左子树的左子树上）

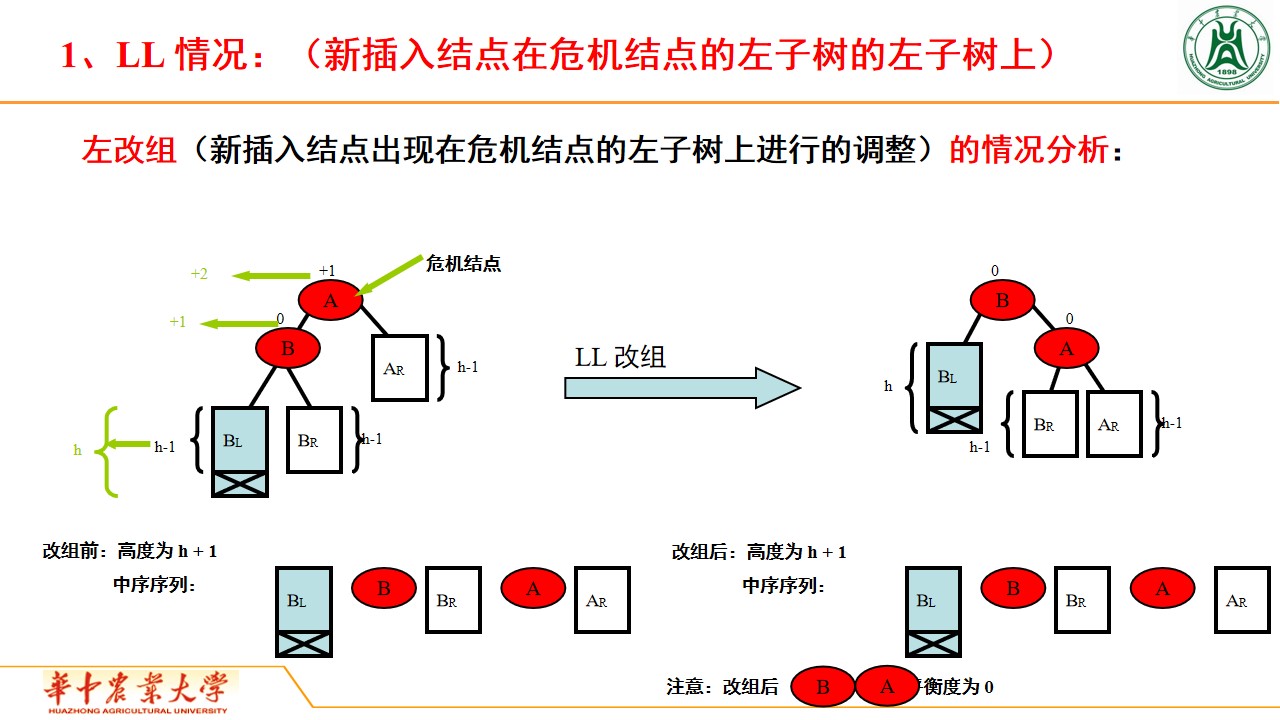
RR型

LR型

RL型

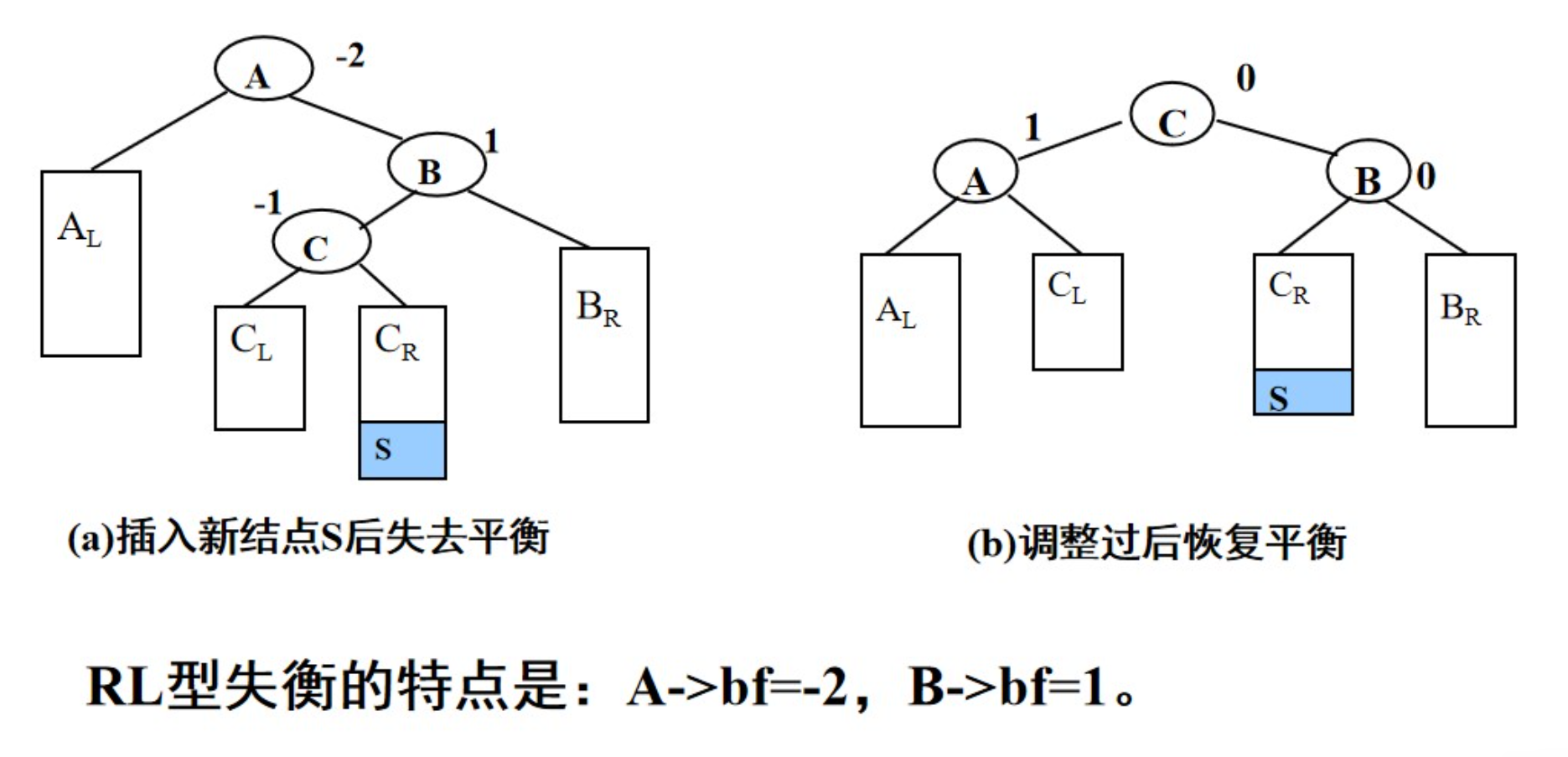
#include <bits/stdc++.h>
#define endl '\n'
using namespace std;
// 首先定义结构体
struct node {
    int data;
    int tag;
    struct node* left_child;
    struct node* right_child;
};

// 然后定义类型别名
typedef struct node* tree;

// 获取二叉树节点的高度
int get_height(tree node) {
    // 如果节点为空，返回高度0
    if (!node) return 0;
    // 递归计算左右子树的高度，取最大值并加1（当前节点）
    return max(get_height(node->left_child), get_height(node->right_child)) + 1;
}

// 计算节点的平衡因子
int get_balance_factor(tree node) {
    // 如果节点为空，返回平衡因子0
    if (!node) return 0;
    // 返回左子树高度减去右子树高度
    return get_height(node->left_child) - get_height(node->right_child);
}

tree right_rotate(tree y) {
    // x指向y的左子节点
    tree x = y->left_child;
    // T2指向x的右子节点
    tree T2 = x->right_child;

    // 将y作为x的右子节点
    x->right_child = y;
    // 将T2作为y的左子节点
    y->left_child = T2;

    // 返回新的根节点x
    return x;
}

tree left_rotate(tree x) {
    // y指向x的右子节点
    tree y = x->right_child;
    // T2指向y的左子节点
    tree T2 = y->left_child;

    // 将x作为y的左子节点
    y->left_child = x;
    // 将T2作为x的右子节点
    x->right_child = T2;

    // 返回新的根节点y
    return y;
}

tree insert(tree node, int key) {
    if (!node) {
        struct node* newNode = new struct node();  
        newNode->data = key;
        newNode->left_child = newNode->right_child = nullptr;
        return newNode;
    }

    // 如果key小于当前节点的值，递归插入到左子树
    if (key < node->data)
        node->left_child = insert(node->left_child, key);
    // 如果key大于当前节点的值，递归插入到右子树
    else if (key > node->data)
        node->right_child = insert(node->right_child, key);
    // 如果key等于当前节点的值，直接返回当前节点（不允许重复值）
    else
        return node;

    // 获取当前节点的平衡因子
    int balance = get_balance_factor(node);

    // Left Left Case：左子树过高且新节点插入在左子树的左子树
    if (balance > 1 && key < node->left_child->data)
        return right_rotate(node);

    // Right Right Case：右子树过高且新节点插入在右子树的右子树
    if (balance < -1 && key > node->right_child->data)
        return left_rotate(node);

    // Left Right Case：左子树过高且新节点插入在左子树的右子树
    if (balance > 1 && key > node->left_child->data) {
        node->left_child = left_rotate(node->left_child);
        return right_rotate(node);
    }

    // Right Left Case：右子树过高且新节点插入在右子树的左子树
    if (balance < -1 && key < node->right_child->data) {
        node->right_child = right_rotate(node->right_child);
        return left_rotate(node);
    }

    // 返回当前节点（不需要旋转的情况）
    return node;
}

tree build_tree(vector<int>& arr, int n) {
    tree root = nullptr;
    for (int i = 1; i <= n; i++) {
        root = insert(root, arr[i]);
    }
    return root;
}

// 打印二叉树的辅助函数
void print_tree_helper(tree node, int space) {
    const int COUNT = 4;  // 每层的缩进量
    if (node == nullptr) return;

    // 先打印右子树
    space += COUNT;
    print_tree_helper(node->right_child, space);

    // 打印当前节点
    cout << endl;
    for (int i = COUNT; i < space; i++)
        cout << " ";
    cout << node->data << "\n";

    // 最后打印左子树
    print_tree_helper(node->left_child, space);
}

// 打印二叉树的接口函数
void print_tree(tree root) {
    print_tree_helper(root, 0);
}

int main(){
    int n;cin >> n;
    vector<int>arr(n+1,0);
    for(int i = 1;i <= n;i++){
        cin >> arr[i];
    }
    tree root = build_tree(arr,n);
    
    // 添加使用root的代码，例如打印树的高度
    cout << "Tree height: " << get_height(root) << endl;
    
    // 打印二叉树
    cout << "\nBinary Tree Structure:\n";
    print_tree(root);

    return 0;
}

总结：

AVL 树的构造可以总结为以下几个关键步骤：

插入节点：在 AVL 树中插入新节点时，按照二叉搜索树的规则找到插入位置，并插入节点。然后，从插入节点到根节点的路径上检查每个祖先节点的平衡因子，如果出现不平衡情况，通过旋转操作进行调整。
删除节点：在 AVL 树中删除节点时，按照二叉搜索树的规则找到要删除的节点，并进行节点删除。接着从删除节点到根节点的路径上检查每个祖先节点的平衡因子，如果有不平衡情况，通过旋转操作进行调整。
旋转操作：AVL 树的旋转操作包括左旋、右旋、左右旋和右左旋，通过这些旋转操作可以保持树的平衡性。具体的旋转操作根据节点的失衡情况和旋转方向进行选择，以恢复树的平衡。
平衡因子更新：在进行插入、删除和旋转操作后，需要更新每个节点的平衡因子，并根据新的平衡因子再次检查是否需要进行旋转操作。
构造过程迭代：在插入和删除节点时，可能需要进行多次旋转操作才能恢复树的平衡。因此，AVL 树的构造过程是一个不断迭代调整节点平衡因子和进行旋转操作的过程。

总的来说，AVL 树的构造过程通过不断调整平衡因子、进行旋转操作和更新节点信息来维护树的平衡性，从而确保 AVL 树具有较好的查找性能和平衡性。

B树

1、B树的定义

B 树（B-tree）是一种自平衡的搜索树，能够保持数据有序。这种数据结构能够让查找数据、顺序访问、插入数据及删除的动作，都在对数时间内完成。B 树的每个节点可以拥有两个以上的子节点，因此 B 树是一种多路搜索树。

2、查找过程

B树是一种多路搜索树，其查找过程与二叉搜索树有所不同。

#include <iostream>
#include <vector>

using namespace std;

const int MAX_KEYS = 3;
const int MAX_CHILDREN = MAX_KEYS + 1;

struct Node {
    vector<int> keys;
    vector<Node*> children;
    Node* parent;

    Node() {
        parent = nullptr;
    }

    bool isLeaf() {
        return children.empty();
    }
};

class BTree {
private:
    Node* root;

    Node* search(Node* node, int key) {
        int i = 0;
        while (i < node->keys.size() && key > node->keys[i]) {
            i++;
        }
        if (i < node->keys.size() && key == node->keys[i]) {
            return node;
        } else if (node->isLeaf()) {
            return nullptr;
        } else {
            return search(node->children[i], key);
        }
    }

public:
    BTree() {
        root = new Node();
    }

    Node* search(int key) {
        return search(root, key);
    }
};

int main() {
    BTree btree;

    // Insert some keys into the B-tree
    // (Not shown here as it's not relevant to the search process)

    // Search for a key in the B-tree
    Node* result = btree.search(10);
    if (result) {
        cout << "Key 10 found in the B-tree\n";
    } else {
        cout << "Key 10 not found in the B-tree\n";
    }

    return 0;
}

在这个示例中，我们定义了一个B树的基本结构和操作，其中包含一个search函数用于查找给定的关键字。

3、插入

向B树中插入一个数据，可能会导致节点的数据变满，即不满足上面提到的节点数据数量在[t,2t-1]这个性质。此时需要对节点进行分裂节点操作：

将数据变满（即节点数据量为2t）的节点，分为左右两个数据量分别为t-1的节点，同时将中间的数据提升到父节点的合适位置上。
如果父节点由于新增了这个被提升的数据导致了变满，就继续上面的分裂节点操作。
沿着树向上一直执行该操作，直到不再变满为止。

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

const int MAX_KEYS = 3;
const int MIN_KEYS = MAX_KEYS / 2;
const int MAX_CHILDREN = MAX_KEYS + 1;

struct Node {
    vector<int> keys;
    vector<Node*> children;
    Node* parent;

    Node() {
        parent = nullptr;
    }

    bool isLeaf() {
        return children.empty();
    }
};

class BTree {
private:
    Node* root;

    Node* splitNode(Node* node) {
        Node* newNode = new Node();
        int mid = node->keys.size() / 2;

        // Move keys and children to the new node
        newNode->keys.assign(node->keys.begin() + mid + 1, node->keys.end());
        node->keys.erase(node->keys.begin() + mid, node->keys.end());

        if (!node->isLeaf()) {
            newNode->children.assign(node->children.begin() + mid + 1, node->children.end());
            for (Node* child : newNode->children) {
                child->parent = newNode;
            }
            node->children.erase(node->children.begin() + mid + 1, node->children.end());
        }

        // Insert mid key and promote to parent node
        int midKey = node->keys[mid];
        if (node->parent) {
            int index = 0;
            while (index < node->parent->keys.size() && midKey > node->parent->keys[index]) {
                index++;
            }
            node->parent->keys.insert(node->parent->keys.begin() + index, midKey);
            node->parent->children.insert(node->parent->children.begin() + index + 1, newNode);
            newNode->parent = node->parent;
        } else {
            Node* newRoot = new Node();
            newRoot->keys.push_back(midKey);
            newRoot->children.push_back(node);
            newRoot->children.push_back(newNode);
            node->parent = newRoot;
            newNode->parent = newRoot;
            root = newRoot;
        }

        return newNode;
    }

    void insertNonFull(Node* node, int key) {
        int i = node->keys.size() - 1;
        if (node->isLeaf()) {
            node->keys.push_back(0); // Make room for the new key
            while (i >= 0 && key < node->keys[i]) {
                node->keys[i + 1] = node->keys[i];
                i--;
            }
            node->keys[i + 1] = key;
        } else {
            while (i >= 0 && key < node->keys[i]) {
                i--;
            }
            i++;
            if (node->children[i]->keys.size() == MAX_KEYS) {
                Node* splitChild = splitNode(node->children[i]);
                if (key > node->keys[i]) {
                    i++;
                }
            }
            insertNonFull(node->children[i], key);
        }
    }

public:
    BTree() {
        root = new Node();
    }

    void insert(int key) {
        Node* node = root;
        if (node->keys.size() == MAX_KEYS) {
            Node* newRoot = new Node();
            newRoot->children.push_back(root);
            root->parent = newRoot;
            root = newRoot;
            splitNode(node);
        }
        insertNonFull(root, key);
    }
};

int main() {
    BTree btree;

    // Insert keys into the B-tree
    btree.insert(10);
    btree.insert(20);
    btree.insert(5);
    btree.insert(15);

    return 0;
}

4、删除

B树的删除操作相对复杂，因为删除可能导致节点的合并或者重新平衡。下面是一个简单的C++实现B树的删除过程：

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

const int MAX_KEYS = 3;
const int MIN_KEYS = MAX_KEYS / 2;
const int MAX_CHILDREN = MAX_KEYS + 1;

struct Node {
    vector<int> keys;
    vector<Node*> children;
    Node* parent;

    Node() {
        parent = nullptr;
    }

    bool isLeaf() {
        return children.empty();
    }
};

class BTree {
private:
    Node* root;

    Node* findSuccessor(Node* node) {
        Node* current = node->children[node->keys.size()];
        while (!current->isLeaf()) {
            current = current->children[0];
        }
        return current;
    }

    void borrowKeyFromPrev(Node* node, int keyIndex) {
        Node* child = node->children[keyIndex];
        Node* sibling = node->children[keyIndex - 1];

        child->keys.insert(child->keys.begin(), node->keys[keyIndex - 1]);
        node->keys[keyIndex - 1] = sibling->keys.back();

        if (!sibling->isLeaf()) {
            child->children.insert(child->children.begin(), sibling->children.back());
            sibling->children.back()->parent = child;
            sibling->children.pop_back();
        }

        sibling->keys.pop_back();
    }

    void borrowKeyFromNext(Node* node, int keyIndex) {
        Node* child = node->children[keyIndex];
        Node* sibling = node->children[keyIndex + 1];

        child->keys.push_back(node->keys[keyIndex]);
        node->keys[keyIndex] = sibling->keys.front();

        if (!sibling->isLeaf()) {
            child->children.push_back(sibling->children.front());
            sibling->children.front()->parent = child;
            sibling->children.erase(sibling->children.begin());
        }

        sibling->keys.erase(sibling->keys.begin());
    }

    void mergeNodes(Node* node, int keyIndex) {
        Node* child = node->children[keyIndex];
        Node* sibling = node->children[keyIndex + 1];
        
        child->keys.push_back(node->keys[keyIndex]);

        for (int i = 0; i < sibling->keys.size(); i++) {
            child->keys.push_back(sibling->keys[i]);
            if (!sibling->isLeaf()) {
                child->children.push_back(sibling->children[i]);
                sibling->children[i]->parent = child;
            }
        }

        if (!sibling->isLeaf()) {
            child->children.push_back(sibling->children.back());
            sibling->children.back()->parent = child;
        }

        node->keys.erase(node->keys.begin() + keyIndex);
        node->children.erase(node->children.begin() + keyIndex + 1);

        delete sibling;
    }

    void deleteFromNode(Node* node, int key) {
        int keyIndex = 0;
        while (keyIndex < node->keys.size() && key > node->keys[keyIndex]) {
            keyIndex++;
        }

        if (keyIndex < node->keys.size() && key == node->keys[keyIndex]) { // Key found in current node
            if (node->isLeaf()) {
                node->keys.erase(node->keys.begin() + keyIndex);
            } else {
                Node* successor = findSuccessor(node);
                node->keys[keyIndex] = successor->keys[0];
                deleteFromNode(successor, successor->keys[0]);
            }
        } else { // Key not found in current node
            if (node->isLeaf()) {
                cout << "Key " << key << " not found in the B-tree" << endl;
                return;
            }

            if (node->children[keyIndex]->keys.size() >= MIN_KEYS + 1) { // Case 3: Key in child has at least t keys
                deleteFromNode(node->children[keyIndex], key);
            } else { // Cases 1 and 2: Merge, borrow or recurse
                // Try borrowing from left sibling
                if (keyIndex > 0 && node->children[keyIndex - 1]->keys.size() >= MIN_KEYS + 1) {
                    borrowKeyFromPrev(node, keyIndex);
                } 
                // Try borrowing from right sibling
                else if (keyIndex < node->keys.size() && node->children[keyIndex + 1]->keys.size() >= MIN_KEYS + 1) {
                    borrowKeyFromNext(node, keyIndex);
                } 
                // Merge with left sibling
                else if (keyIndex > 0) {
                    mergeNodes(node, keyIndex - 1);
                    deleteFromNode(node->children[keyIndex - 1], key);
                } 
                // Merge with right sibling
                else {
                    mergeNodes(node, keyIndex);
                    deleteFromNode(node->children[keyIndex], key);
                }
            }
        }
    }

public:
    BTree() {
        root = new Node();
    }

    void insert(int key) {
        // Insertion implementation goes here
    }

    void remove(int key) {
        if (root->keys.empty()) {
            cout << "B-tree is empty, cannot delete key" << endl;
            return;
        }

        deleteFromNode(root, key);
    }

    void printInOrder(Node* node) {
        if (node) {
            for (int i = 0; i < node->keys.size(); i++) {
                printInOrder(node->children[i]);
                cout << node->keys[i] << " ";
            }
            printInOrder(node->children.back());
        }
    }

    void print() {
        cout << "B-tree keys in order: ";
        printInOrder(root);
        cout << endl;
    }
};

int main() {
    BTree btree;

    // Insert keys into the B-tree
    btree.insert(10);
    btree.insert(20);
    btree.insert(5);
    btree.insert(15);
    btree.insert(25);
    btree.insert(13);
    btree.insert(16);

    btree.print();

    // Delete key from the B-tree
    btree.remove(20);

    btree.print();

    return 0;
}

在这个示例中，我们定义了B树的删除过程。当删除一个关键字时，需要考虑节点合并、节点分裂等情况。您可以根据需要扩展此代码，例如添加搜索操作或其他功能。

哈希表

一、Hash 表

哈希表（Hash Table）是一种数据结构，用于实现关联数组（Associative Array）或映射（Map）这类抽象数据类型。哈希表通过利用哈希函数（Hash Function）来将关键字（Key）映射到存储位置的数组中，以实现快速的查找、插入和删除操作。

哈希表的定义通常包括以下几个主要组件：

哈希函数（Hash Function）：哈希函数接受一个关键字作为输入，然后计算出该关键字对应的哈希值。哈希函数应该将不同的关键字映射到不同的哈希值，但也可能存在不同关键字映射到相同哈希值的情况（哈希冲突）。
哈希表（Hash Table）：哈希表是一个存储哈希桶（Hash Bucket）或槽位（Slot）的数组。每个槽位可以存储一个键值对或者指向存储键值对的链表或其他数据结构的指针。
键值对（Key-Value Pair）：在哈希表中存储的数据通常采用键值对的形式，其中键是用来进行查找的搜索键，值则是关联到该键的数据。
哈希冲突处理：由于哈希函数可能导致不同的关键字映射到同一个位置，因此需要解决哈希冲突问题。解决哈希冲突的常用方法包括链地址法（Separate Chaining）、开放寻址法（Open Addressing）等。

总的来说，哈希表提供了快速的数据访问效率，平均情况下，查找、插入和删除操作的时间复杂度为 O(1)。在需要高效的查找操作时，哈希表是一种常用且重要的数据结构。

二、哈希函数的构造方法

哈希函数是哈希表中最关键的部分，它确定了键值如何映射到哈希表的槽位上。以下是几种常见的哈希函数构造方法：

直接选址法（Direct Addressing）：直接选址法是一种简单的哈希函数构造方法，直接将关键字作为哈希值。例如，对于一个整数关键字 k，哈希函数可以简单地返回 k 作为哈希值，即 h(k) = k。
数字分析法（Digit Analysis）：数字分析法适用于关键字为数字串的情况。通过观察数字串的分布情况，选取其中几位作为哈希值。例如，对于一个电话号码，可以选取其中几个数字作为哈希值。
折叠法（Folding Method）：折叠法将关键字分割成若干段，然后将这些段相加或者进行其他运算，得到最终的哈希值。例如，对于一个长数字串，可以将其分割成若干段，然后相加得到哈希值。
平方取中法（Mid-square Method）：平方取中法适用于整数关键字。首先对关键字进行平方运算，然后取平方结果的中间几位数作为哈希值。例如，对于关键字 k，哈希函数可以计算 h(k) = (k^2 / 100) % 10000
除留余数法（Division Method）：除留余数法是一种常见的哈希函数构造方法。将关键字除以一个数（通常是哈希表的大小）取余数作为哈希值。例如，对于整数关键字 k，哈希函数可以计算 h(k) = k % m，其中 m 是哈希表的大小。

以上是常见的一些哈希函数构造方法，根据不同的应用场景和数据特点，选择适合的哈希函数非常重要。良好设计的哈希函数应该具有高效的散列性能，尽可能避免哈希冲突，并保持均匀的散列结果分布。

三、冲突的处理

1、线性探测法

2、二次探测法

3、随机探测法

4、拉链法

在哈希表中，冲突指的是当两个不同的键被映射到了同一个哈希表的槽位上。冲突的处理是设计一个解决冲突的机制，以确保哈希表的性能和正确性。其中一种常见的冲突处理方法是拉链法（Chaining），也被称为链地址法。

在拉链法中，每个哈希表的槽位维护一个链表（或者其他数据结构，如红黑树）来存放发生冲突的键值对。当发生冲突时，新的键值对会被插入到链表中。这样，同一个哈希槽中可以存放多个键值对，每个哈希槽对应一个链表。

下面是拉链法处理冲突的基本步骤：

初始化哈希表，为每个槽位创建一个空链表。
当需要插入一个键值对时，首先计算该键对应的哈希值，并找到对应的槽位。
如果槽位上已经有键值对存在，执行下一步；否则，将新的键值对插入到槽位对应的链表中。
遍历链表，查找是否已经存在相同的键。若存在相同的键，则更新其对应的值；否则，将新的键值对插入链表末尾。

拉链法的优点是简单且容易实现，适用于动态变化的哈希表，因为可以动态调整链表的长度。然而，链表的查询操作需要遍历整个链表，可能导致性能下降。在实际应用中，通常需要根据具体情况选择适当的冲突处理方法，以确保哈希表的性能和效率。

#include <iostream>
#include <vector>
#include <list>
#include <string>

// 定义一个结构体表示键值对
struct KeyValuePair {
    std::string key;
    int value;
};

// 定义哈希表类
class HashTable {
private:
    static const int TABLE_SIZE = 10;
    std::vector<std::list<KeyValuePair>> table;

    // 哈希函数，这里使用简单的除留余数法
    int hashFunction(const std::string& key) {
        int hash = 0;
        for(char ch : key) {
            hash += ch;
        }
        return hash % TABLE_SIZE;
    }

public:
    HashTable() {
        table.resize(TABLE_SIZE);
    }

    // 插入键值对到哈希表
    void insert(const std::string& key, int value) {
        int index = hashFunction(key);
        for(auto& pair : table[index]) {
            if(pair.key == key) {
                pair.value = value; // 如果键已经存在，则更新对应的值
                return;
            }
        }
        table[index].push_back({key, value}); // 在链表末尾插入新的键值对
    }

    // 查找键对应的值
    int get(const std::string& key) {
        int index = hashFunction(key);
        for(auto& pair : table[index]) {
            if(pair.key == key) {
                return pair.value;
            }
        }
        return -1; // 找不到对应的键，返回一个特殊值
    }
};

int main() {
    HashTable hashTable;

    // 插入键值对到哈希表
    hashTable.insert("apple", 5);
    hashTable.insert("orange", 8);
    hashTable.insert("banana", 3);

    // 查找键对应的值
    std::cout << "Value of 'apple': " << hashTable.get("apple") << std::endl;
    std::cout << "Value of 'grape': " << hashTable.get("grape") << std::endl;

    return 0;
}