)
O(\rho|Q|)
O(ρ∣Q∣)），当
∣
Q
∣
|Q|
∣Q∣很大的时候（比如
n
2
n^2
n2），这个误差没什么意义，那么我们可以得到大量查询下仍旧有意义的误差吗？
这是可以的，使用boosting技术可以实现一个差分隐私算法，对于每个回答误差大致为
O
(
ρ
n
log
3
/
2
∣
Q
∣
)
O(\rho\sqrt{n}\log^{3/2}|Q|)
O(ρn
log3/2∣Q∣)！并且针对线性查询，该算法运行时间可以变为多项式时间。
算法概述
简单叙述一下这个算法，它有T轮迭代，在每一轮当中，
- 我们根据分布
D
t
\mathcal{D}_t
Dt选出来k个query，然后送到bsg(base synopsis generator)里面，bsg返回对于所有query的回答。
2. 我们对于bsg给出的回答做个评判，然后分别打个分，越准确的回答，对应系数
a
t
,
q
a_{t,q}
at,q约大。
3. 归一化打分，把它作为一个分布更新。
T轮之后，我们得到了
T
∣
Q
∣
T|Q|
T∣Q∣个结果，对于每个query选一个好的回答，返回。
整个算法流程大致就是这样，然后有几个比较有趣的点。
- bsg是什么？bsg有四个参数（
k
k
k,
λ
\lambda
λ,
η
\eta
η,
β
\beta
β），分别构建所需要的查询数量，回答误差，平衡参数，失败概率。代表简单地说，他是一个黑盒，你给他k个query，它就能给你一系列回答，对于这k个query有着比较好的近似。然后有一个事实，如果k个query是从一个分布里选的，那对k个query的良好近似，可以得到对于
∣
Q
∣
|Q|
∣Q∣个query里面重要的（分值高的，或者是分布概率大的）有着良好近似。
2. 和boosting区别在哪？可以看到我们对于回答的质量，并不仅仅用
λ
\lambda
λ来衡量，而是
λ
\lambda
λ和
λ
μ
\lambda+\mu
λ+μ两个阈值来衡量。在中间区域，我们根据回答的误差来更新。以上操作均是因为需要保证DP。
3. 如果你仔细观察
u
t
,
q
u_{t,q}
ut,q你就会发现，生成的
D
\mathcal{D}
D和指数机制有着密切联系。
OK，现在我们得到了一系列回答，对于Q里面那些重要的查询有着比较好的回答，那么之后干的事情就是在做boosting，也就是核心技术，得到对于所有
q
∈
Q
q\in Q
q∈Q的良好回答。简单地说，把一个weak回答器，变成strong回答器。
总结
给大家的福利
零基础入门
对于从来没有接触过网络安全的同学，我们帮你准备了详细的学习成长路线图。可以说是最科学最系统的学习路线，大家跟着这个大的方向学习准没问题。
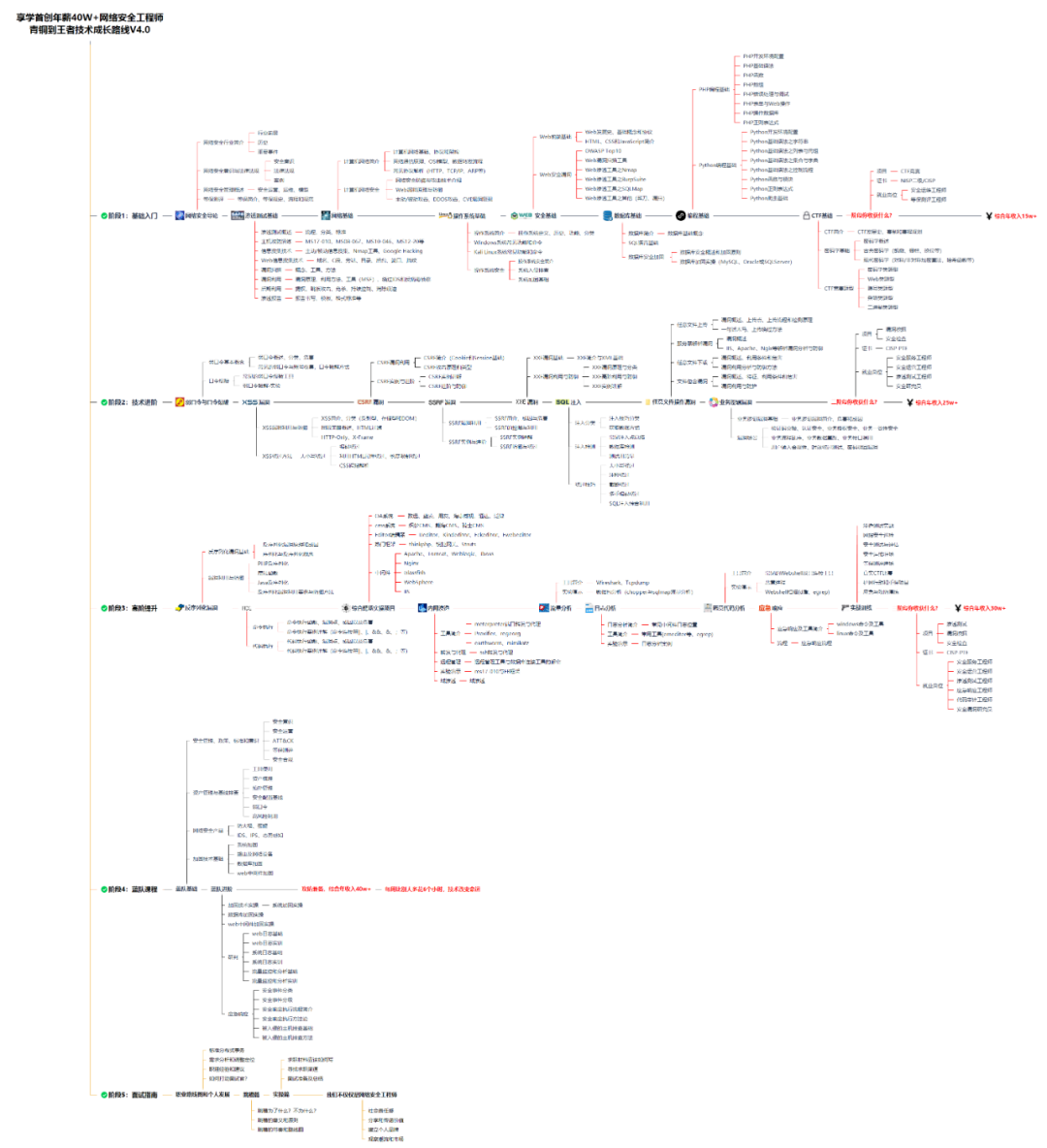
同时每个成长路线对应的板块都有配套的视频提供：
因篇幅有限，仅展示部分资料
网络安全面试题
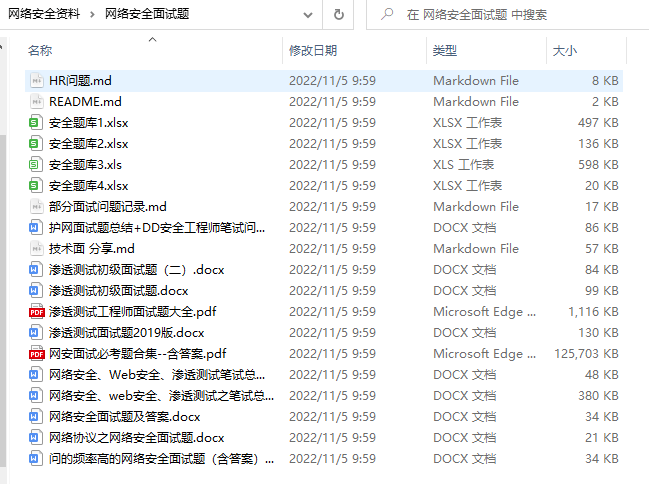
绿盟护网行动
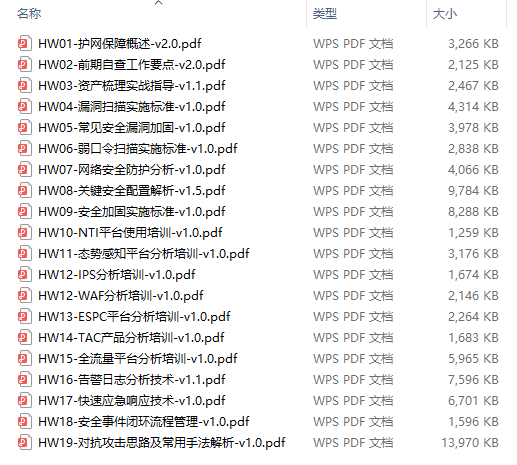
还有大家最喜欢的黑客技术
网络安全源码合集+工具包
所有资料共282G，朋友们如果有需要全套《网络安全入门+黑客进阶学习资源包》，可以扫描下方二维码领取（如遇扫码问题，可以在评论区留言领取哦）~
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
