【数据结构与算法】——二叉树OJ题

前言

了解完二叉树基础知识后，来刷一些典型OJ题吧，
如：单值二叉树、相同二叉树、对称二叉树、另一棵树的子树……
如果知识点有问题复习一下吧：二叉树

正文

1.二叉树的算法题

1.2 [单值二叉树]

(https://leetcode.cn/problems/univalued-binary-tree/description/)
题目：

单值二叉树要求每个结点都有相同的值， 1、如果二叉树是空树，即为二叉树
2.节点值比较：查看左子节点是否存在，若存在且其值和根节点值不同，就返回 false；同样查看右子节点是否存在，若存在且其值和根节点值不同，也返回 false。
3.递归检查：对左子树和右子树分别递归调用 isUnivalTree 函数，只有当左右子树都是单值二叉树时，整棵树才是单值二叉树，所以返回两者的逻辑与结果。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool isUnivalTree(struct TreeNode* root) {
    if(root == NULL)
    {
        return true;
    }
    if(root->left&&root->val != root->left->val)
    {
        return false;
    }
    if(root->right&&root->val != root->right->val)
    {
        return false;
    }

    return isUnivalTree(root->left)&&isUnivalTree(root->right);
}

这里有人可能问，能不能把！=改成==，false改成true？不能，当节点值相等时，我们不能直接返回 true，因为还需要递归检查子树的情况。不过可以把判断逻辑改成当节点值不相等时直接返回 false，相等时继续递归检查。如

if (root->left) {
        if (root->val == root->left->val) {
            // 若左子节点值和根节点值相同，继续递归检查左子树
            if (!isUnivalTree(root->left)) {
                return false;
            }
        } else {
            // 若左子节点值和根节点值不同，直接返回 false
            return false;
        }
    }

显然这样很麻烦。

1.2 [相同的树]

(https://leetcode.cn/problems/same-tree/)

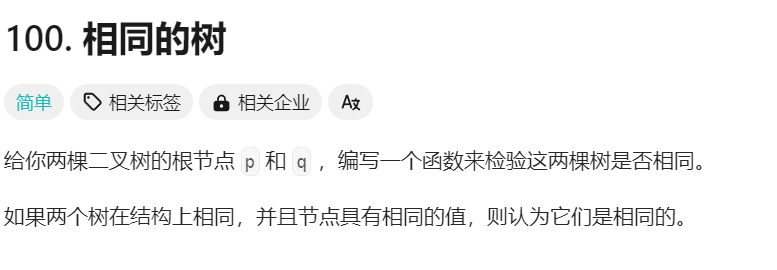
1.若两个二叉树都为空树，则相同
2.若一个二叉树为空一个不为空，肯定不是
3.从头结点开始，比较val值是否相同，不同直接 return false
4.若当前结点val值相同，同时递归两个二叉树左子树和两个二叉右子树，当其中之一或全部为空时，递归结束，返回最终结果

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
    if(p == NULL&&q == NULL)
    {
        return true;
    }
    if(p == NULL||q == NULL)
    {
        return false;
    }
    if(p->val != q->val)
    {
        return false;
    }
    return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}

画了个图自己理解一下（二叉树的题目一定要画图！！！！）

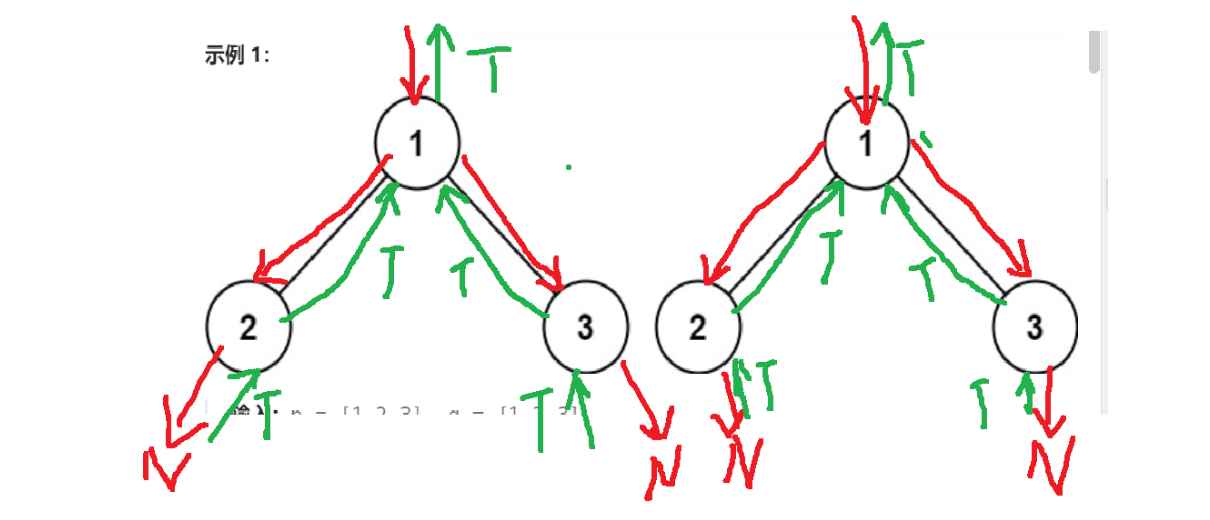
拓展：[对称二叉树]

(https://leetcode.cn/problems/symmetric-tree/submissions/622617856/)

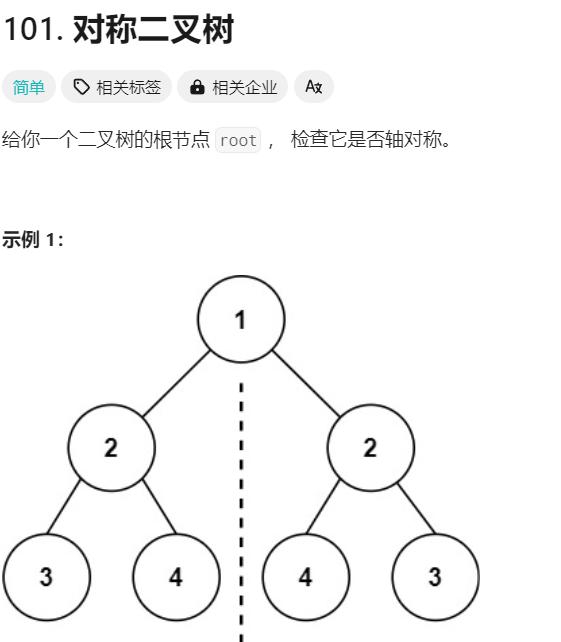
这道题和前面一道题十分相似
简单说一下思路：
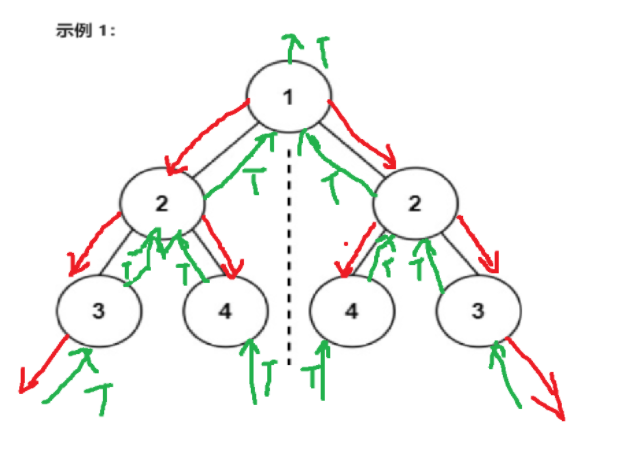
1.一个二叉树，从头结点开始，需要检查左子树的左子节点和右子树的右子节点是否相等，以及左子树的右子节点和右子树的左子节点是否相等。
2.直接把之前相等的代码拿下来，不过递归的参数改为左子树的左子节点和右子树的右子节点
3.对称函数中，利用相等函数递归左右字数，这里因为不是递归isSymmetric对称函数，所以不需要终止条件

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

 bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
    if(p == NULL&&q == NULL)
    {
        return true;
    }
    if(p == NULL||q == NULL)
    {
        return false;
    }
    if(p->val != q->val)
    {
        return false;
    }
    return isSameTree(p->left,q->right)&&isSameTree(p->right,q->left);
}
bool isSymmetric(struct TreeNode* root) {
    return isSameTree(root->left,root->right);
}

1.3 [另一棵树的子树]

(https://leetcode.cn/problems/subtree-of-another-tree/description/)

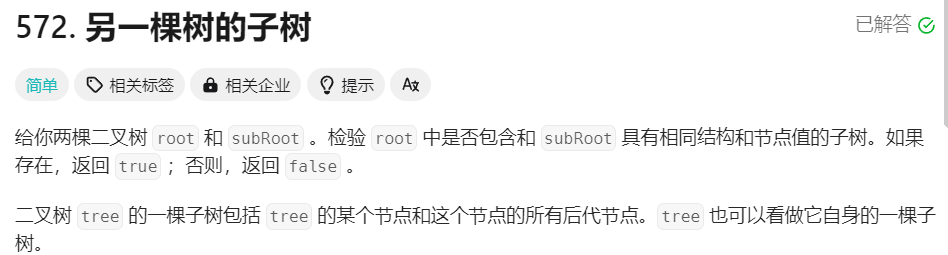
如下图root的左子树=subRoot

这道题似乎也和判断而二叉树的相等有关系，那么我们给出这样一种思路：从头结点开始，判断两个二叉树是否相等（利用之前的思路），若相等，返回true，不过不相等，分别递归左右子树，如果找到相等的子树则返回true，||有其一即可
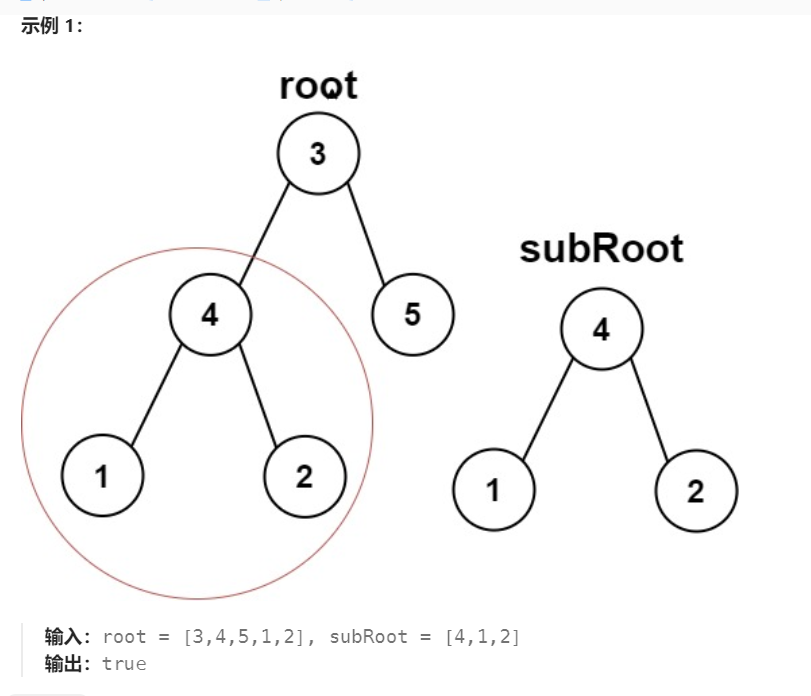
但要注意的是：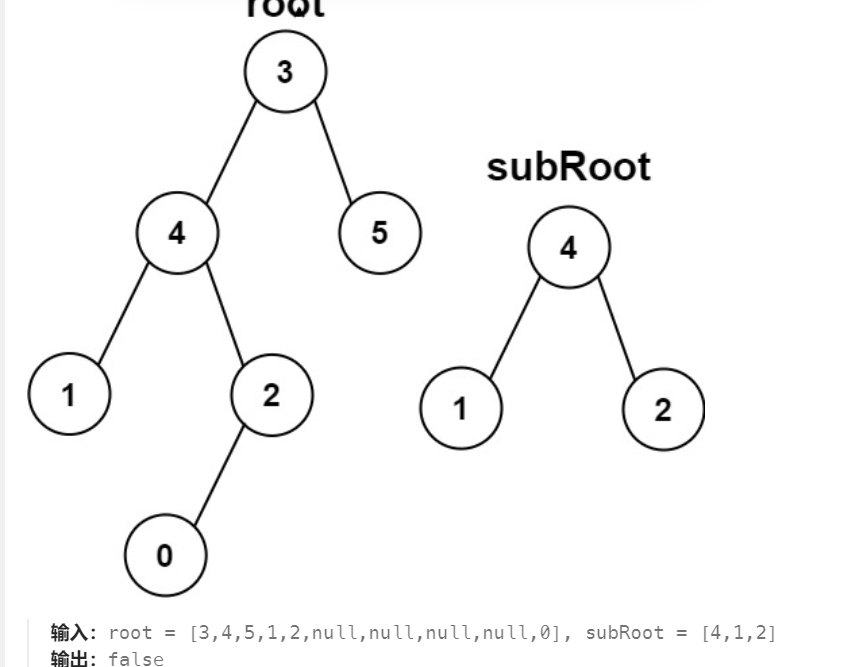
这种不算，因为subRoot的2的后继为NULL,两者不同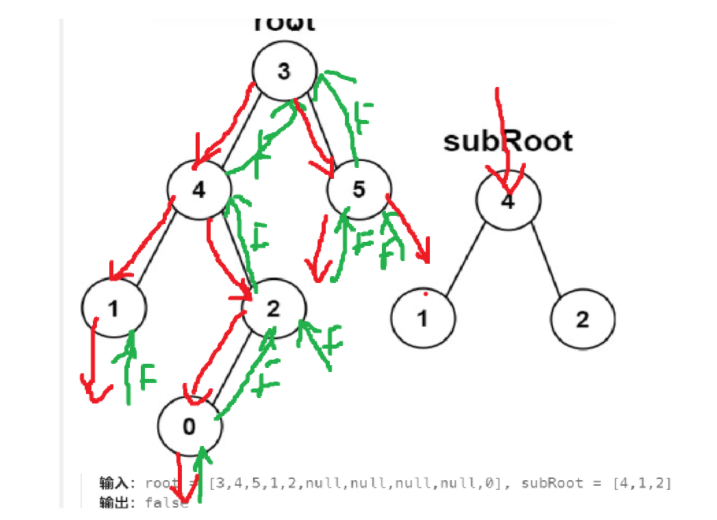

1. 辅助函数 sisame
   功能：判断两棵二叉树是否完全相同（结构和节点值均一致）。
   思路：若两棵树当前节点均为空，返回 true（空树相等）。
   若其中一棵树当前节点为空而另一棵不为空，返回 false（结构不一致）。
   若当前节点值不同，返回 false（值不一致）。
   递归检查左右子树是否完全相同。
2. 辅助函数 sisame
   功能：判断两棵二叉树是否完全相同（结构和节点值均一致）。
   思路：若两棵树当前节点均为空，返回 true（空树相等）。
   若其中一棵树当前节点为空而另一棵不为空，返回 false（结构不一致）。
   若当前节点值不同，返回 false（值不一致）。
   递归检查左右子树是否完全相同。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

bool sisame(struct TreeNode* root, struct TreeNode* subRoot){
    if(root == NULL && subRoot ==NULL)
        return true;

    if(root==NULL || subRoot ==NULL)
        return false;
    
    if(root->val != subRoot->val)
        return false;
    
    return sisame(root->left,subRoot->left) && sisame(root->right,subRoot->right);
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) {
    if(root == NULL)
        return false;
    if(subRoot == NULL)
        return true;
    
    if(sisame(root,subRoot))
        return true;

    return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}

1.4 [二叉树的前序遍历]

(https://leetcode.cn/problems/binary-tree-preorder-traversal/)（前中后序遍历）

这道OJ题和之前那篇文章不太一样，因为给出的函数参数不一样，我们还需要序节点个数
1.计算节点个数：节点个数 = 根节点（1）+左子树结点个数+右子树结点个数
2.前序遍历：先将节点值存入arr中，注意因为每次递归都会销毁栈帧，所以我们直接将arr[i]中的i作为参数传递其地址，保证其正常++，将值存入。
3.完成题目代码：为arr创建内存，调用函数，最后返回arr
如果这几种方法还有问题，看我这篇文章：二叉树

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
 typedef struct TreeNode TreeNode;
 int treeSize(TreeNode* root)
 {
    if(root == NULL)
    {
        return 0;
    }
    return 1+treeSize(root->right)+treeSize(root->left);
 }
void order(TreeNode* root,int*arr,int*pi)
 {
    if(root == NULL)
    {
        return;
    }
    arr[(*pi)++] = root->val;
    order(root->left,arr,pi);
    order(root->right,arr,pi);
 }
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
    *returnSize = treeSize(root);
    int* arr = (int *)malloc(sizeof(int)*(*returnSize));
    int i = 0;
    order(root,arr,&i);
    return arr;
}

至于，其他的两道题目：中序遍历和后序遍历，我想已经会写了，没错，就是将
这三行调换顺序即可，不明白的可以看这篇文章：二叉树

	arr[(*pi)++] = root->val;
    order(root->left,arr,pi);
    order(root->right,arr,pi);

1.5 [二叉树的构建和遍历]

(https://www.nowcoder.com/practice/4b91205483694f449f94c179883c1fef)

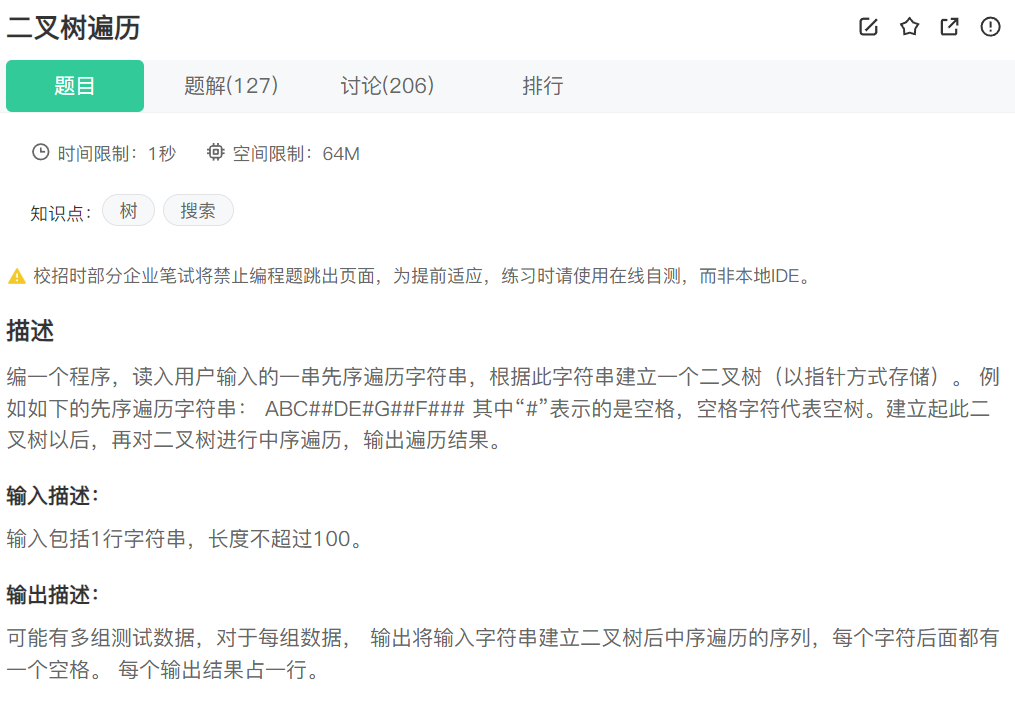
思路比较简单：先序遍历->构建二叉树->中序遍历

1. 定义二叉树节点结构
   定义了一个二叉树节点的结构体 TreeNode，包含一个字符类型的数据域 data 用于存储节点的值，以及两个指针域 left 和 right 分别指向左子节点和右子节点。
2. 创建新节点
   buyNode 函数用于动态分配一个新的二叉树节点。它接收一个字符参数 ch，将其作为节点的数据域。如果内存分配失败，使用 perror 函数输出错误信息并终止程序。初始化节点的左右子节点指针为 NULL 后返回该节点。
3. 根据前序遍历序列创建二叉树
   createTree 函数是创建二叉树的核心函数，采用递归的方式根据前序遍历序列构建二叉树。使用一个指针 pi 来跟踪当前处理的字符位置。如果当前字符是 #，表示该位置为空节点，指针 pi 后移并返回 NULL；否则，创建一个新节点，指针 pi 后移，递归调用 createTree 函数分别创建左子树和右子树。
4. 中序遍历二叉树
   inOrder 函数实现了二叉树的中序遍历（左 根 右）。如果当前节点为空，直接返回；否则，先递归遍历左子树，输出当前节点的值，再递归遍历右子树。

#include <stdio.h>
#include <stdlib.h> 

typedef struct TreeNode{
    char data;
    struct TreeNode* left;
    struct TreeNode* right;
}TreeNode;

TreeNode* buyNode(char ch)
{
    TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));
    if(node == NULL)
    {
        exit(1);
    }
    node->data = ch;
    node->left = node->right = NULL;
    return node;
}

TreeNode* createTree(char* arr,int* pi)
{
    if(arr[*pi] == '#')
    {
        (*pi)++;
        return NULL;
    }
    TreeNode* root = buyNode(arr[*pi]);
    (*pi)++;
    root->left = createTree(arr, pi);
    root->right = createTree(arr,pi);

    return root;
}

// 中序 -- 左根右
void inOrder(TreeNode* root)
{
    if(root == NULL)
    {
        return;
    }
    inOrder(root->left);
    printf("%c ",root->data);
    inOrder(root->right);
}

int main()
{
    // 读取输入的前序遍历字符串
    char arr[100];
    scanf("%s",arr);
    // 根据前序遍历字符串创建二叉树
    int i = 0;
    TreeNode* root = createTree(arr, &i);
    // 二叉树的中序遍历
    inOrder(root);
    return 0;
}

2.二叉树选择题

二叉树性质

对于任何一棵二叉树，若度为0的叶结点个数为 (n0)，度为2的分支结点个数为 (n2)，则满足：
[n0 = n2 + 1]

证明：
假设二叉树中度为2的结点数为 (a)，度为1的结点数为 (b)，叶结点数为 (c)。

• 二叉树的边数可通过结点度计算：总边数 = (2a + b)
• 二叉树的边数也可通过结点总数计算：总边数 = 结点总数 - 1 = (a + b + c - 1)
  联立得：(2a + b = a + b + c - 1)，化简后 (a = c - 1)，即 (n_0 = n_2 + 1)。

选择题

1. 题目：某二叉树共有399个结点，其中有199个度为2的结点，则该二叉树中的叶子结点数为（ ）
   • A. 不存在这样的二叉树
   • B. 200
   • C. 198
   • D. 199

套公式：[n0 = n2 + 1]
答案：B

2. 题目：在具有2n个结点的完全二叉树中，叶子结点个数为（ ）

   • A. n
   • B. n+1
   • C. n-1
   • D. n/2
     解答：n0+n1+n2 = 2n
     套公式：2n0+n1=2n
     我们知道一个完全二叉树度为一的结点可能有0个或1个，如图：
     
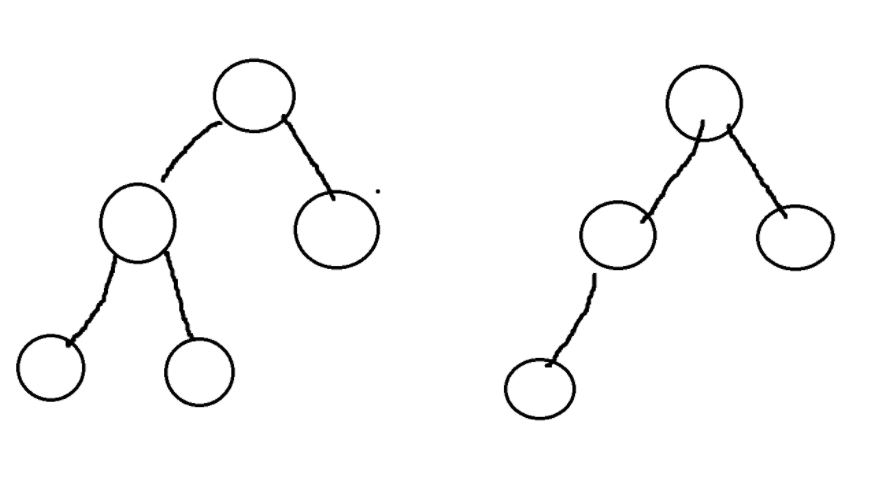
     所以0或1代入，结点数必须是整数，得出结果。
     答案：A

3. 题目：一棵完全二叉树的结点数为531个，那么这棵树的高度为（ ）

   • A. 11
   • B. 10
   • C. 8
   • D. 12
     

   答案：B

4. 题目：一个具有767个结点的完全二叉树，其叶子结点个数为（ ）

   • A. 383
   • B. 384
   • C. 385
   • D. 386
     答案：B

链式二叉树遍历选择题

先自己做然后看后面思路

1. 题目：某完全二叉树按层次输出（同一层从左到右）的序列为ABCDEFGH，该完全二叉树的前序序列为（ ）

   • A. ABDHECFG
   • B. ABCDEFGH
   • C. HDBEAFCG
   • D. HDEBFGCA
     答案：A

2. 题目：二叉树的先序遍历和中序遍历如下：先序遍历为EFHIGJK，中序遍历为HFIEJKG，则二叉树根结点为（ ）

   • A. E
   • B. F
   • C. G
   • D. H
     答案：A

3. 题目：设一棵二叉树的中序遍历序列为badce，后序遍历序列为bdeca，则二叉树前序遍历序列为（ ）

   • A. adbce
   • B. decab
   • C. debac
   • D. abcde
     答案：D

4. 题目：某二叉树的后序遍历序列与中序遍历序列相同，均为ABCDEF，则按层次输出（同一层从左到右）的序列为（ ）

   • A. FEDCBA
   • B. CBAFED
   • C. DEFCBA
   • D. ABCDEF
     答案：A

链式二叉树遍历选择题解题思路

第一题

1. 构建完全二叉树结构：
   • 层次遍历按层从左到右填充结点，完全二叉树的结点编号严格遵循从上到下、从左到右的顺序。
   • 根结点为 A（第1层），第2层左到右为 B、C，第3层为 D、E、F、G，第4层为 H（仅左子树存在）。
2. 前序遍历规则：根 → 左子树 → 右子树。
   • 根 A 优先访问，然后递归遍历左子树（以 B 为根），再遍历右子树（以 C 为根）。
   • 左子树 B 的左孩子是 D，D 无左孩子，右孩子是 H；B 的右孩子是 E，E 的左孩子是 F，右孩子是 G。
3. 前序序列：A → B → D → H → E → F → G → C，即 ABDHECFG（选项A）。

第二题

1. 先序遍历性质：第一个结点为根结点。
   • 先序序列 EFHIGJK 的第一个结点是 E，因此根结点为 E。 （秒了）
2. 验证中序遍历：
   • 中序遍历以根结点 E 为中心，左子树为 HFI，右子树为 JKG，符合二叉树结构。
     答案：A（E）

第三题

1. 后序遍历性质：最后一个结点为根结点。
   • 后序序列 bdeca 的最后一个结点是 a，故根结点为 a。
2. 划分中序左右子树：
   • 中序序列 badce 中，a 左侧为左子树 b，右侧为右子树 dce。
3. 递归处理右子树：
   • 右子树后序序列为 bdeca 去掉 a 和左子树 b，剩余 deca，最后一个结点 c 为右子树的根。
   • 中序右子树 dce 中，c 左侧为 d，右侧为 e。
4. 构建树结构：
   • 根 a → 左孩子 b，右孩子 c；c 的左孩子 d，右孩子 e。
5. 前序遍历规则：根 → 左 → 右，序列为 a → b → c → d → e，即 abcde（选项D）。

第四题

• 思路：
  1. 后序与中序相同的条件：
     • 后序遍历顺序为“左 → 右 → 根”，中序为“左 → 根 → 右”。若两者相同，则所有结点 没有右子树（否则中序的“根”和“右”顺序会与后序不同）。
  2. 树结构：
     • 树为 左斜树，每个结点只有左孩子，最后一个结点 F 是根（后序最后一个结点）。
     • 结点层次关系：F 是根，E 是 F 的左孩子，D 是 E 的左孩子，依此类推，形成 F ← E ← D ← C ← B ← A 的左链。
  3. 层次遍历规则：从上到下、从左到右。
     • 根结点 F 在第1层，E 在第2层，D 在第3层，C 在第4层，B 在第5层，A 在第6层。
  4. 层次序列：F, E, D, C, B, A，即 FEDCBA（选项A）。

总结

• 先序遍历：根结点为序列首元素，用于快速定位根。
• 后序遍历：根结点为序列尾元素，用于划分左右子树。
• 中序遍历：通过根结点分割左右子树，递归构建树结构。
• 完全二叉树：层次序列直接对应结点编号，前序遍历需按“根左右”规则逐层展开。
• 特殊情况：后序与中序相同 ⇒ 无右子树；先序与中序相同 ⇒ 无左子树。