二叉树高频题--part1（不含树型dp）-优快云博客

本文链接：https://blog.youkuaiyun.com/2401_86679269/article/details/144459609

树型dp简介

一，二叉树的层序遍历

把树按一层一层的搜索，访问。

这个问题里我们要放回一个链表，其包含该层所有节点。

之前设计不使用递归实现前后中序二叉树遍历的算法，就是使用栈来完成，用栈来模拟递归函数。

现在我们使用队列，利用先进后出，弹出的节点后，又将它的子节点加入队列中，这样只有在这层访问完后才会访问下一层。

但是问题又出现了：虽然节点访问是按照层进行，但我不知道访问的节点是第几层（如果不给节点增添信息的话）。

错误

1，构造二叉树

代码展示

Node* create_tree(int* arr, int len)
{
	Node* root = new Node(arr[0]);

	for (int i = 1; i < len; i++)
	{
		Node* current = root;
		Node* pre = root;
		while (current)
		{
			pre = current;
			if (arr[i] <= current->value)
			{
				current = current->left;
			}
			else
			{
				current = current->right;
			}
		}

		Node* newNode = new Node(arr[i]);
		if (!pre->left) pre->left = newNode;
		else pre->right = newNode;
	}

	return root;
}

你会发现，我的代码构造的二叉树是会先将所在层填满后再往下一层添加。

修改

Node* newNode = new Node(arr[i]);
if (arr[i] <= pre->value) pre->left = newNode;
else pre->right = newNode;

2，范围循环

3，链表插入

unordered_map<int,Node*> ans;
ans[level].next = newNode;

这么链接节点会丢失节点

所有选择数据结构list

代码

#include<iostream>
#include<queue>
#include<unordered_map>
#include<list>

using namespace std;

struct Node
{
	int value;
	Node* left;
	Node* right;

	Node(int x) : value(x), left(NULL), right(NULL) {};
};



Node* create_tree(int* arr, int len)
{
	Node* root = new Node(arr[0]);

	for (int i = 1; i < len; i++)
	{
		Node* current = root;
		Node* pre = root;
		while (current)
		{
			pre = current;
			if (arr[i] <= current->value)
			{
				current = current->left;
			}
			else
			{
				current = current->right;
			}
		}

		Node* newNode = new Node(arr[i]);
		if (arr[i] <= pre->value) pre->left = newNode;
		else pre->right = newNode;
	}

	return root;
}

class Search
{
private:
	queue<Node*> myqueue;
	unordered_map<int, int> record;
	unordered_map<int, list<int>> ans;

public:

	Search(Node* root)
	{ 
		myqueue.push(root); 
		record[root->value] = 0;
	};

	void search()
	{
		Node* cur;
		
		while (!myqueue.empty())
		{
			cur = myqueue.front();
			myqueue.pop();
			int level = record.find(cur->value)->second;
			record.erase(cur->value);
			ans[level].push_back(cur->value);

			if (cur->left)
			{
				record.insert({ cur->left->value,level + 1 });
				myqueue.push(cur->left);
			}
			if (cur->right)
			{
				record.insert({ cur->right->value,level + 1 });
				myqueue.push(cur->right);
			}
		}
	}

	void print_ans()
	{
		for (const auto& list : ans)
		{
			cout << "the level of " << list.first << " :";
			for (const auto& node : list.second)
			{
				cout << node << " ";
			}
			cout << endl;
		}
	}
};


void preOrder_traverse(Node* root)
{
	if (!root) return;
	cout << root->value << " ";
	preOrder_traverse(root->left);
	preOrder_traverse(root->right);
}


int main()
{
	int arr[] = { 5,1,4,7,3,9,10,6,8,2 };
	int len = sizeof(arr) / sizeof(int);
	Node* root = create_tree(arr, len);

	Search bfs(root);
	bfs.search();
	bfs.print_ans();
	return 0;
}

二，加强版

使用数组来实现队列

class Queue
{
private:
	Node* arr[100] = { 0 };
	int head, tail;
	int remain = 100;
	//head和tail是数组索引，但模拟队列头和尾
public:

	Queue() :head(0), tail(0) {};
	bool empty()
	{
		if (remain == 100) return true;
		else return false;
	}

	Node* front()
	{
		return arr[head];
	}

	void pop()
	{
		head = (head + 1) % 100;
		remain++;
	}

	void push(Node* input)
	{
		if (remain < 1)
		{
			cout << "no room !" << endl;
			return;
		}
		arr[tail] = input;
		tail = (tail + 1) % 100;
		remain--;
	}
};

利用有限的数组设置队列，通过变量remain来判断队列是否满，从而避免头尾相碰。

后面也是直接将queue<Node*> myqueue 改为Queue myqueue就行。

再改进

在已知树节点的个数，这样可以确定数组队列大小。

代码

#include<iostream>
#include<queue>
#include<unordered_map>
#include<list>

using namespace std;

struct Node
{
	int value;
	Node* left;
	Node* right;

	Node(int x) : value(x), left(NULL), right(NULL) {};
};


Node* create_tree(int* arr, int len);


class Search
{
private:
	Node* arr[10];
	unordered_map<int, int> record;
	unordered_map<int, list<int>> ans;

public:
	int head, tail;
	

	void search(Node* root)
	{
		head = tail = 0;
		int level = 0;
		arr[tail++] = root;

		while (head < tail)
		{
			int size = tail - head;
			list<int> newlist;
			//size决定了接下来进行几次操作。
			for (int i = 0; i < size; i++)
			{
				Node* temp = arr[head++];
				newlist.push_back(temp->value);
				//这是将队列里的节点加入到答案节点。

				if (temp->left)arr[tail++] = temp->left;
				if (temp->right)arr[tail++] = temp->right;
				//将队列里的节点的子节点加入队列中。
			}
			//在执行完这个for循环后，该层的所有节点都完成了遍历，
			// 同时下一层的节点全部都加入到队列中去了
			ans.insert({ level++,newlist });

			//为了避免head和tail最后抵达边界
			//就要使用环形队列。
		}
	}

	void print_ans()
	{
		for (const auto& it : ans)
		{
			cout << "Level " << it.first << " :";
			for (const auto& node : it.second)
			{
				cout << node << " ";
			}
			cout << endl;
		}
	}
};



int main()
{
	int arr[] = { 5,1,4,7,3,9,10,6,8,2 };
	int len = sizeof(arr) / sizeof(int);
	Node* root = create_tree(arr, len);

	Search bfs;
	bfs.search(root);
	bfs.print_ans();
	return 0;
}


Node* create_tree(int* arr, int len)
{
	Node* root = new Node(arr[0]);

	for (int i = 1; i < len; i++)
	{
		Node* current = root;
		Node* pre = root;
		while (current)
		{
			pre = current;
			if (arr[i] <= current->value)
			{
				current = current->left;
			}
			else
			{
				current = current->right;
			}
		}

		Node* newNode = new Node(arr[i]);
		if (arr[i] <= pre->value) pre->left = newNode;
		else pre->right = newNode;
	}

	return root;
}

如果害怕数组越界，可以参考前面的使用remain表示剩余空间的方法。

三，二叉树的锯齿形层序遍历

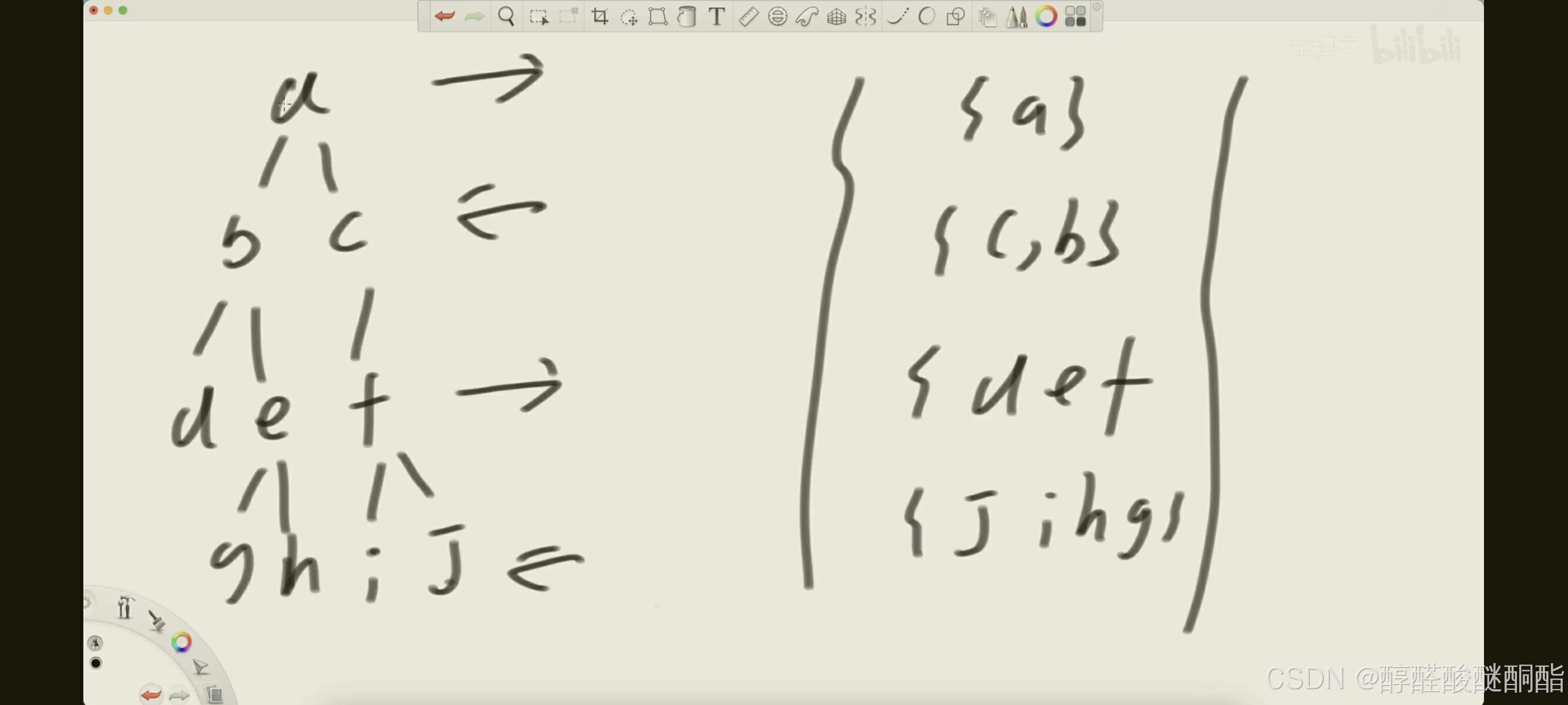
蛇形遍历吧

如果不嫌烦的话，可以像上面的层序遍历一样，只是有了翻转链表的过程。

1，使用数组队列

错误

a，

for (int i = reverse ? tail - 1 : head, int j = reverse ? -1 : 1, int k = 0;
	k < size; i += j, k++)
{
	Node* cur = arr[i];
	newlist.push_back(cur->value);
}

变量声明只需要一个类型标识符。

b，

忘记更新reverse，导致一直从左往右遍历。

代码

void search(Node* root)
{
	bool reverse = false;
	//当reverse为false，代表从左往右遍历；为true，代表从右往左遍历。
	int level = 0;
	head = tail = 0;
	arr[tail++] = root;

	while (head < tail)
	{
		int size = tail - head;
		list<int> newlist;

		//如果是false，就是从左到右，head……tail-1，索引增。
		//如果是true，就是从右到左，tail-1……head，索引减。
		for (int i = reverse ? tail - 1 : head, j = reverse ? -1 : 1, k = 0;
			k < size; i += j, k++)
		{
			Node* cur = arr[i];
			newlist.push_back(cur->value);
		}
		//完成了该层节点的遍历。

		//下面是为下次宽度遍历做准备，由size决定操作次数，
		// 要将多少个子节点加入到队列中
		for (int i = 0; i < size; i++)
		{
			Node* temp = arr[head++];

			if (temp->left)arr[tail++] = temp->left;
			if (temp->right)arr[tail++] = temp->right;
			//将队列里的节点的子节点加入队列中。
		}
		//在执行完这个for循环后，该层的所有节点都都加入到队列中去了
		ans.insert({ level++,newlist });

		//一定不能忘了更新reverse，我第一次就是忘了导致输出是基础的bfs
		reverse = !reverse;
	}
}

2，使用双向队列

首先看看错误代码

我是看AI给的代码改的，傻B的AI，真不能全信，关键时刻还得靠自己。

void search(Node* root)
{
    deque<Node*> queue;
    bool reverse = true;
    int level = 0;
    queue.push_back(root);
    int size = queue.size();

    while (!queue.empty())
    {
        list<int> newlist;
        for (int i = 0; i < size; i++)
        {
            Node* cur;
            if (reverse)
            {
                cur = queue.front();
                queue.pop_front();
                newlist.push_back(cur->value);
            }
            else
            {
                cur = queue.back();
                queue.pop_back();
                newlist.push_back(cur->value);
            }
            
            if (cur->left)queue.push_back(cur->left);
            if (cur->right)queue.push_back(cur->right);
        }
        
        size = queue.size();
        reverse = !reverse;
        ans[level++] = newlist;
    }
}

错误点在后面插入子节点时，都采用后序插入，如果是从头部访问弹出无影响，但是从尾部就有问题了。

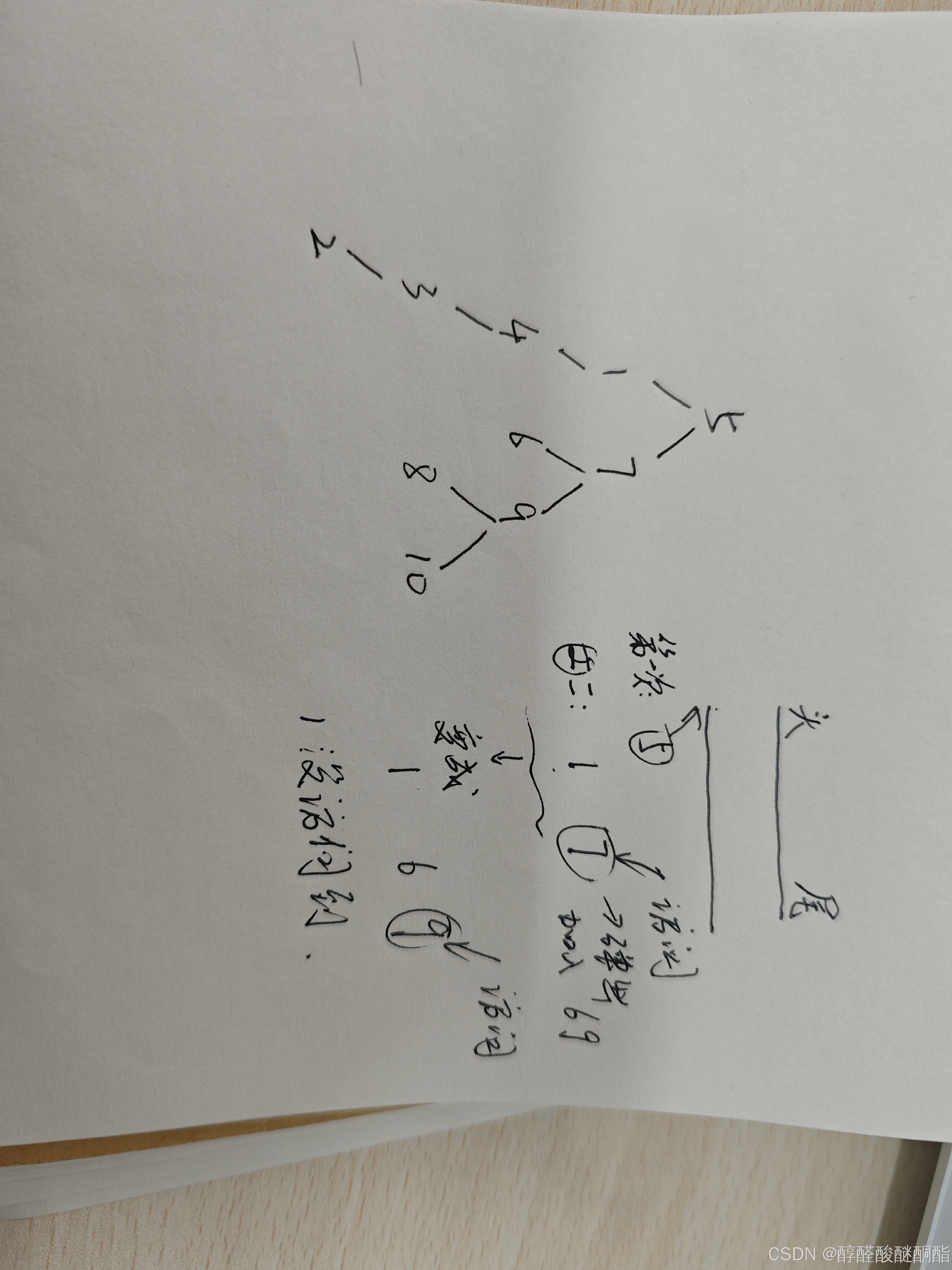
我想了下关键是遍历和加入下层节点两个过程不能冲突，

我想了个办法。也是对上面问题思考，设计算法，一定要像写数学题一样打草稿，不断地试错改进。

解决办法

对于双向队列：

从头访问，从尾加入，先加左后加右子节点；

从尾访问，从头加入，先加右后加左子节点。

代码

void search(Node* root)
{
    deque<Node*> queue;
    bool reverse = true;
    int level = 0;
    queue.push_back(root);
    int size = queue.size();

    while (!queue.empty())
    {
        list<int> newlist;
        for (int i = 0; i < size; i++)
        {
            Node* cur;
            if (reverse)
            {
                cur = queue.front();
                queue.pop_front();
                newlist.push_back(cur->value);
                if (cur->left)queue.push_back(cur->left);
                if (cur->right)queue.push_back(cur->right);
            }
            else
            {
                cur = queue.back();
                queue.pop_back();
                newlist.push_back(cur->value);
                if (cur->right)queue.push_front(cur->right);
                if (cur->left)queue.push_front(cur->left);
            }
            
            
        }
        
        size = queue.size();
        reverse = !reverse;
        ans[level++] = newlist;
    }
}

使用数组方法的话就不用考虑冲突问题，因为使用了临时变量i来访问数组。

四，二叉树的最大的特殊宽度

算每层的宽度，一般都是不考虑空节点。如果考虑空节点，求宽度。

每层计算的起始是从第一个不为空的节点到最后一个不为空的节点。

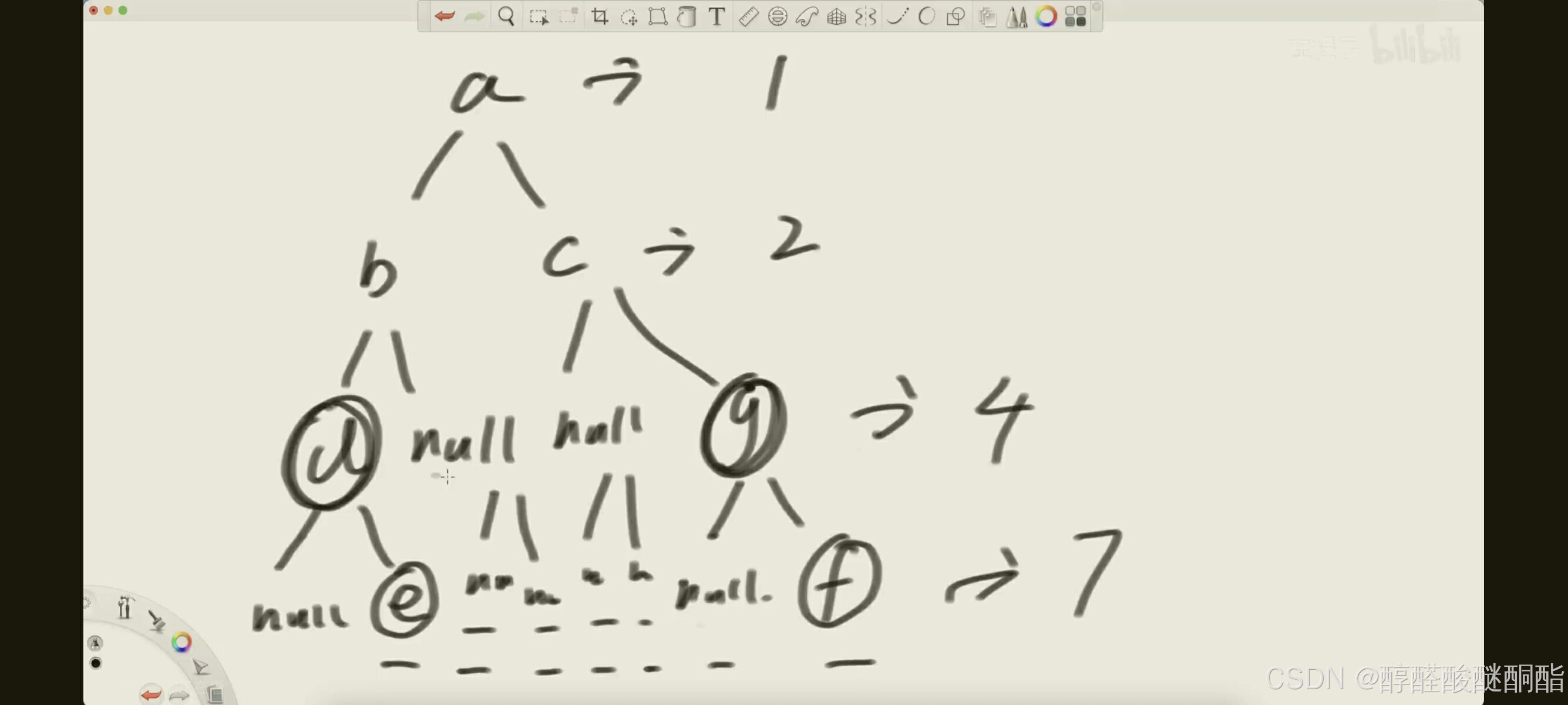
首先我们得了解到之前使用数组实现堆的时候就是利用编号（索引）来找父节点和子节点。

同样我们不需要管哪些空节点，只需要知道节点的编号就可以了。当然我们不可能再用数组来表示树了。所以结构体肯定要多一项属性。

前置知识：

已知该节点的编号是i，则左子节点为2 * i，右为2 * i + 1。

父节点直接就是i / 2。

如果结构体可以自定义话可以用上面方法，但只是单纯给你传入一个树的头节点，你又该怎么办？

步骤

1，遍历每一层，找到最左和最右的节点。

2，准备两个队列，一个队列放节点，一个放节点对应的编号。

（我觉的话也可以用哈希map，如果觉得队列很麻烦的话）

代码

本来自己代码是正确的，我宁愿怀疑AI是错的，后没有怀疑一下我自己，二叉树的图画错了。

#include<iostream>
#include<queue>
#include<list>
#include<unordered_map>

using namespace std;

struct Node
{
    int value;
    Node* left;
    Node* right;

    Node(int x) : value(x), left(NULL), right(NULL) {};
};

Node* create_tree(int* arr, int len);

class Search
{
private:
    queue<Node*> myqueue;
    queue<int> number;
    unordered_map<int, int> ans;
public:
    int level = 0;
    int width = 1;
    
    void traverse(Node* root)
    {
        myqueue.push(root);
        number.push(1);
        while (!myqueue.empty())
        {
            int left = number.front();
            int right = number.back();
            width = right - left + 1;
            ans[level++] = width;

            for (int i = 0; i < myqueue.size(); i++)
            {
                Node* cur = myqueue.front();
                int num = number.front(); // 保存当前节点的序号
                myqueue.pop();
                number.pop();
                if (cur->left) 
                {
                    myqueue.push(cur->left);
                    number.push(2 * num);
                }
                if (cur->right) 
                {
                    myqueue.push(cur->right);
                    number.push(2 * num + 1);
                }
            }
        }
    }

    void print_ans()
    {
        for (const auto& it : ans)
        {
            cout << "Level " << it.first << " :" << it.second << endl;
        }
    }
};

int main()
{
    int arr[] = { 5,1,4,7,3,9,10,6,8,2 };
    int len = sizeof(arr) / sizeof(int);
    Node* root = create_tree(arr, len);

    Search bfs;
    bfs.traverse(root);
    bfs.print_ans();
    return 0;
}


Node* create_tree(int* arr, int len)
{
    Node* root = new Node(arr[0]);

    for (int i = 1; i < len; i++)
    {
        Node* current = root;
        Node* pre = root;
        while (current)
        {
            pre = current;
            if (arr[i] <= current->value)
            {
                current = current->left;
            }
            else
            {
                current = current->right;
            }
        }

        Node* newNode = new Node(arr[i]);
        if (arr[i] <= pre->value) pre->left = newNode;
        else pre->right = newNode;
    }

    return root;
}

当然可以使用数组队列去实现。

五，二叉树的最大深度和最小深度

1，最大深度

原理：使用递归函数，先求左子树的高度，再求右子树的高度，然后左右中大的那一个高度加上1，因为要算上自己这层高度。

代码

int max_depth(Node* root)
{
    if (!root) return 0;
    else
    {
        int a = max_depth(root->left);
        int b = max_depth(root->right);
        return a > b ? a + 1 : b + 1;
    }

2，最小深度

算高度时一定是到叶节点才算结束。必须搜索到方框的数字才截至。

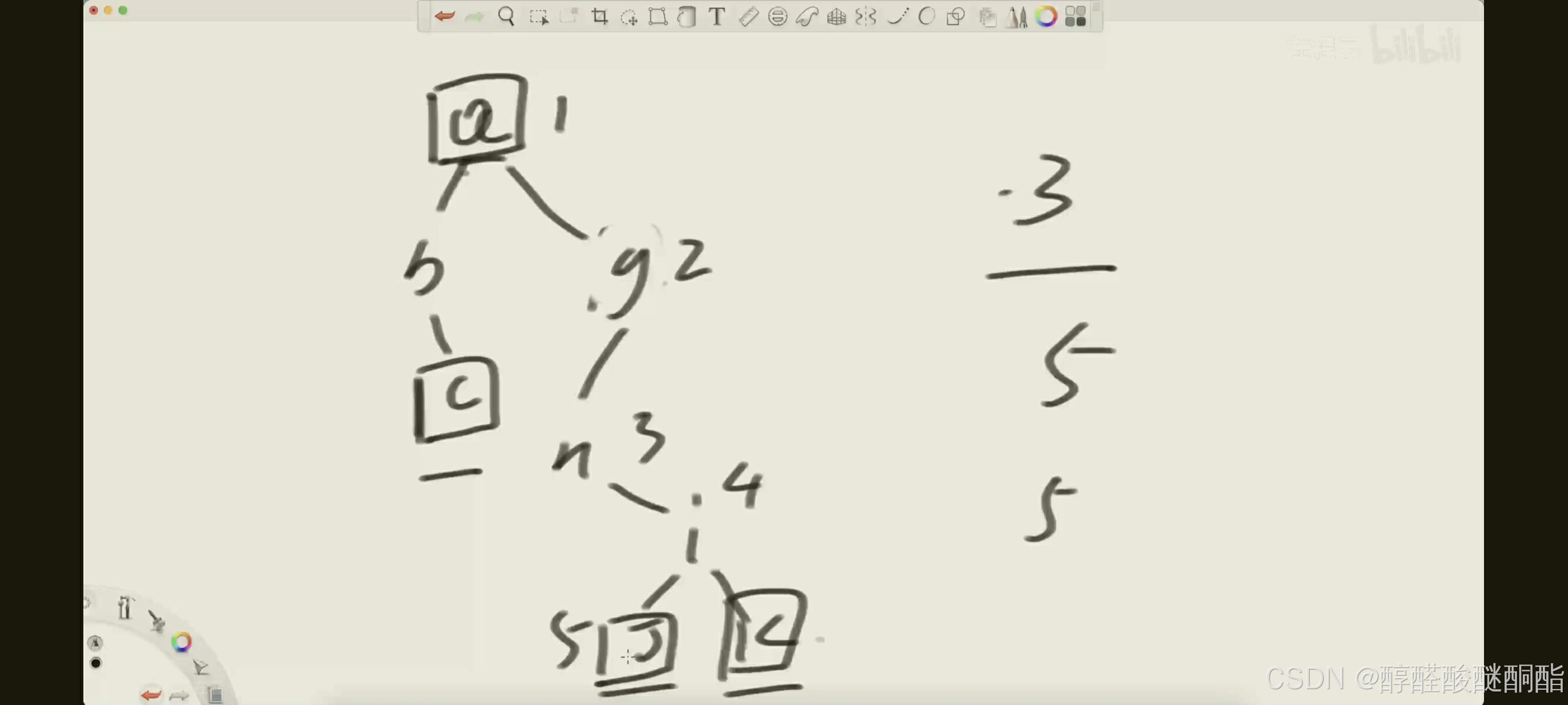
原理：

算左右两边的最小高度，然后取他们中最小的再加1。

注意基准情况。如果为空节点直接返回0，如果左右子节点都为空，直接返回1.

但同时也要注意如果某个节点的左或右节点为空，但另一个子节点存在，就不能最小子树高度为0.

所以开始设置为一个很大的数。

代码

int min_depth(Node* root)
{
    if (!root) return 0;
    //当前树是空树时，直接返回0
    if (!root->left && !root->right) return 1;
    //叶节点直接返回1

    int ldepth = Max;
    int rdepth = Max;
    //当某个节点只有一个子节点时，不能直接调用空节点。所以才有让l，r初始化
    if (root->left) ldepth = min_depth(root->left);
    if (root->right) rdepth = min_depth(root->right);

    return ldepth < rdepth ? ldepth + 1 : rdepth + 1;
}

六，二叉树的先序序列化和反序序列化

1，定义，概念

序列化（Serialization）是指将数据结构或对象转换为一种连续的字节流（byte stream）的过程，这样可以方便地存储或传输数据。反序列化（Deserialization）则是指将字节流转换回原始的数据结构或对象。

在二叉树的序列化中，我们需要将二叉树的结构和节点值转换为一种连续的字节流。二叉树的序列化通常使用以下两种方法：

前序遍历序列化（Preorder Traversal）：先访问根节点，然后递归地访问左子树和右子树。这种方法可以得到一个前序遍历的序列，如：root -> left -> right。
层序遍历序列化（Level Order Traversal）：从根节点开始，逐层访问节点，先访问父节点，然后访问子节点。这种方法可以得到一个层序遍历的序列，如：root -> left -> right -> left-left -> left-right -> right-left -> right-right。

二叉树的序列化可以使用以下步骤：

选择序列化方法：选择前序遍历或层序遍历作为序列化方法。
遍历二叉树：使用选择的序列化方法遍历二叉树，访问每个节点并记录其值和子节点指针。
构造序列化字符串：将访问的节点值和子节点指针转换为一个字符串，使用特定的分隔符（如逗号或空格）分隔每个节点的信息。
存储或传输序列化字符串：将序列化字符串存储在文件中或通过网络传输给其他程序。

反序列化二叉树的过程与序列化相反，我们需要将序列化字符串转换回原始的二叉树结构。这个过程通常涉及以下步骤：

读取序列化字符串：从文件或网络中读取序列化字符串。
解析序列化字符串：使用特定的分隔符分隔每个节点的信息，并解析出节点值和子节点指针。
构造二叉树：使用解析出的节点值和子节点指针构造原始的二叉树结构。

二叉树的序列化和反序列化在很多应用中非常重要，例如：

数据存储：序列化二叉树可以将其存储在文件或数据库中，以便后续使用。
数据传输：序列化二叉树可以将其传输给其他程序或系统，以便共享或协同工作。
算法设计：序列化二叉树可以帮助设计更高效的算法，例如二叉树的查找、插入和删除操作。

2，实现

序列化和反序列化要使用同一套规则。

如果是前序遍历

不同结构的树有不同的字符串表示

如果使用中序遍历，就没有一一对应。

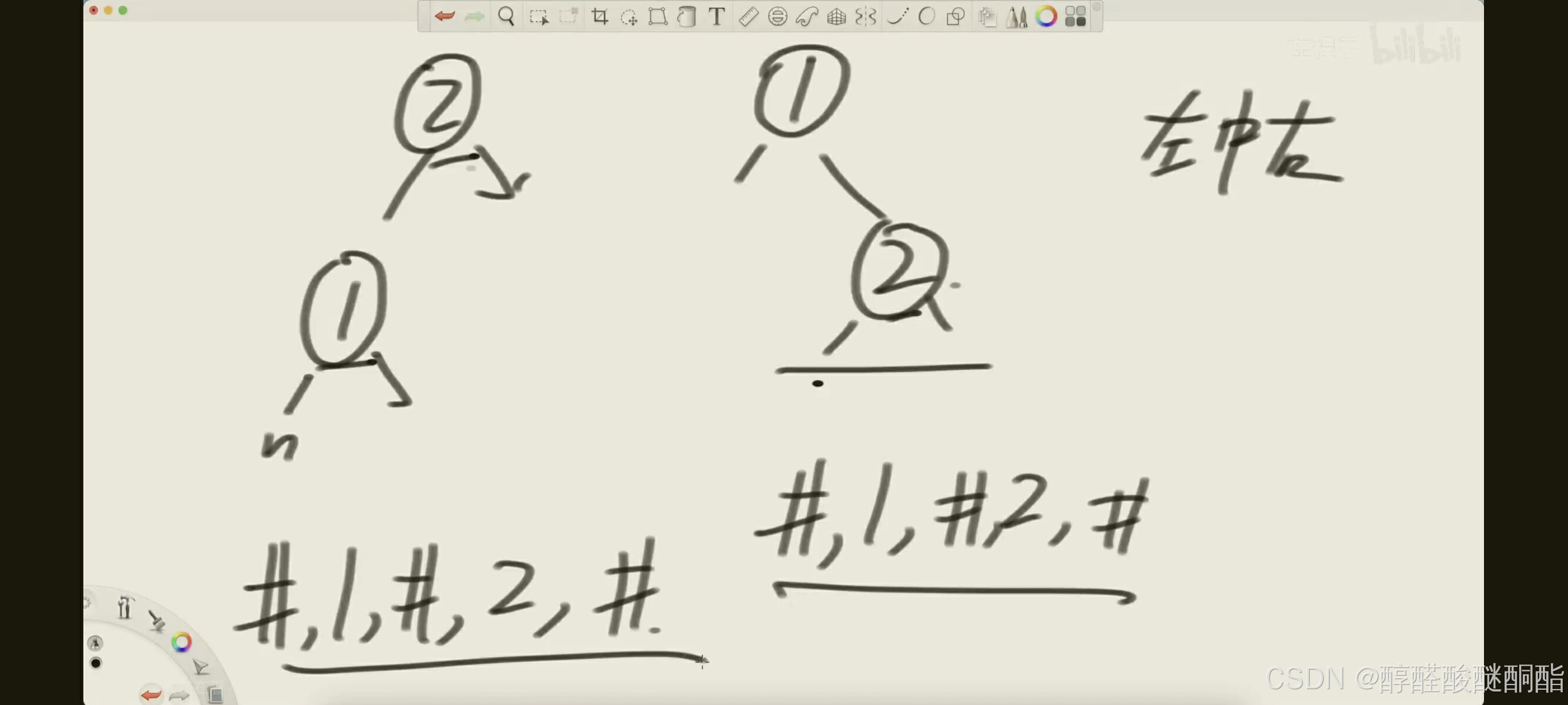
3，补充

高效追加字符串

4，序列化

代码

string serialize(Node* root)
{
    string ans;
    stringstream* str = new stringstream;
    recursion(root, str);
    *str >> ans;
    return ans;

}

void recursion(Node* root, stringstream* str)
{
    //利用先序遍历，第一次到达该节点时进行操作，即序化。
    if (!root)//如果当前节点为空，就用#来表示。
    {
        *str << "#,";
    }
    else
    {
        *str << root->value << ",";
        recursion(root->left,str);
        recursion(root->right, str);
    }
}

结果

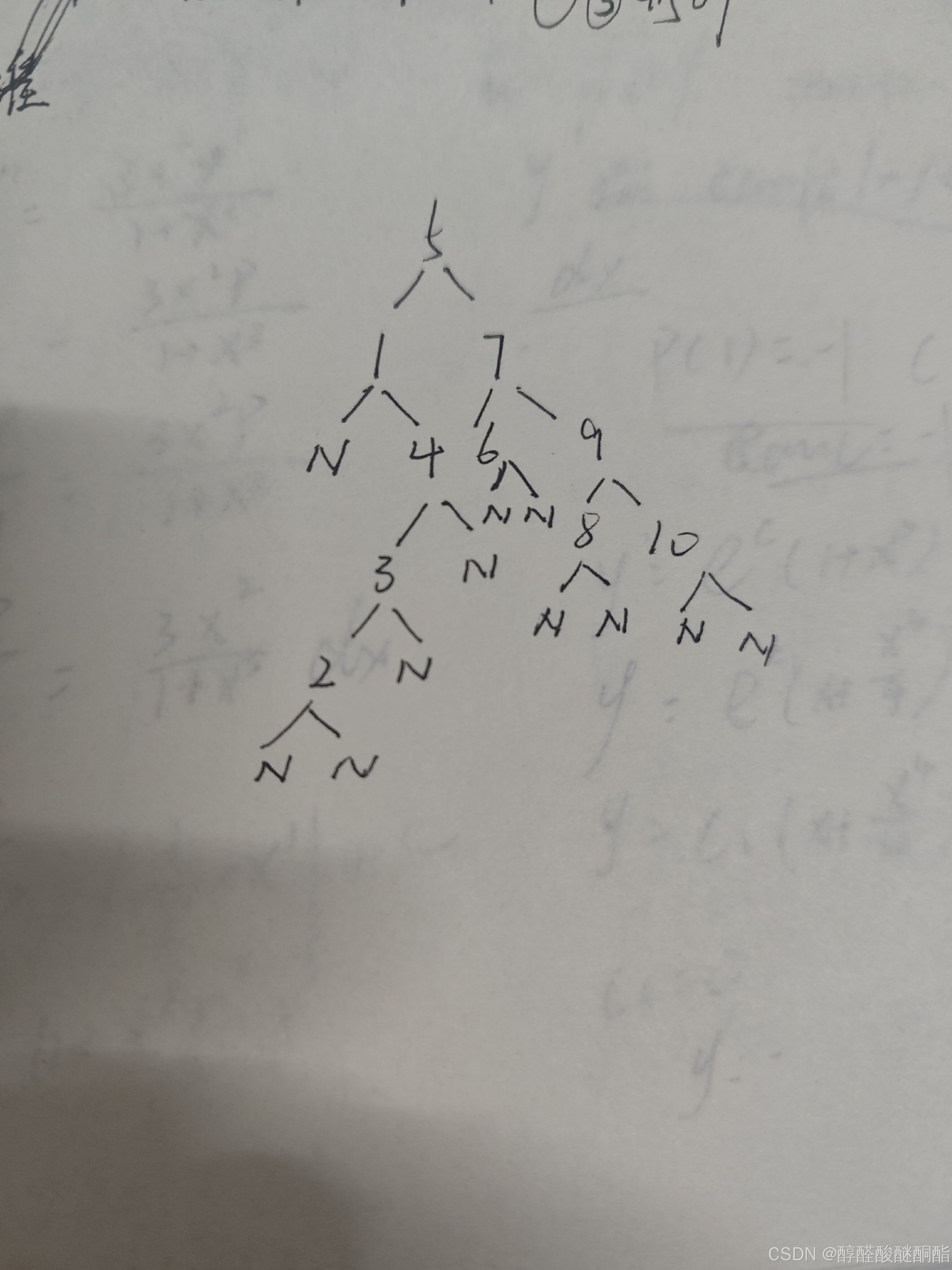
改进

5，反序列化

补充

如何按指定的字符分割字符串。

1）

#include <iostream>
#include <sstream>
#include <vector>
#include <string>

int main() {
    std::string str = "5,1,#,4,3,2,#,#,#,#,7,6,#,#,9,8,#,#,10,#,#";
    std::stringstream ss(str);
    std::string token;
    std::vector<std::string> tokens;
    ss << str;

    while (std::getline(ss, token, ',')) {
        tokens.push_back(token);
    }

    for (const auto& token : tokens) {
        std::cout << token << std::endl;
    }

    return 0;
}

2）

#include<iostream>
#include<vector>
#include<string>
#include<sstream>

using namespace std;

vector<string> split(string& str, char ch);

int main()
{
	stringstream ss;
	string str = "5,1,#,4,3,2,#,#,#,#,7,6,#,#,9,8,#,#,10,#,#";
	string token;
	vector<string> tokens;
	tokens = split(str, ',');
	for (string& it : tokens)
	{
		cout << it << " ";
	}
}

vector<string> split(string& str, char ch)
{
	vector<string> vec;
	int pos = 0, pre = 0;
	do
	{
		pos = str.find(ch,pre);
		if (pos == string::npos) pos = str.length();
		string token = str.substr(pre, pos - pre);
		if (!token.empty()) vec.push_back(token);
		pre = pos + 1;
	} while (pre < str.length());

	return vec;
}

代码

Node* deserialize(string data)
{
    stringstream ss;
    vector<string> tokens;
    string token;
    ss << data;
    while (getline(ss, token, ','))
    {
        tokens.push_back(token);
    }

    cnt = 0;
    return recursion2(tokens);
}

int cnt;
//设置成全局变量，记录当前数组消费到了哪里。
//在其他地方都能影响到cnt，实现向量遍历。
Node* recursion2(vector<string> strs)
{
    if (cnt >= strs.size()) return NULL;
    string cur = strs[cnt++];
    if (cur == "#") return NULL;
    else
    {
        Node* treenode = new Node(stoi(cur));
        //然后去消费左右子树
        treenode->left = recursion2(strs);
        //因为recursion2是有返回值的，所以成功将节点连接，树得以搭建。
        treenode->right = recursion2(strs);
        return treenode;
    }
}

有时使用全局变量就可以避免给函数参数，直接在函数内部修改全局变量。

完整代码

#include<iostream>
#include<string>
#include<sstream>
#include<vector>
using namespace std;

struct Node
{
    int value;
    Node* left;
    Node* right;

    Node(int x) : value(x), left(NULL), right(NULL) {};
};

Node* create_tree(int* arr, int len);
void traverse(Node* root);

class Search
{
public:
    
    string serialize(Node* root)
    {
        string ans;
        stringstream* str = new stringstream;
        recursion1(root, str);
        *str >> ans;
        return ans;

    }

    void recursion1(Node* root, stringstream* str)
    {
        //利用先序遍历，第一次到达该节点时进行操作，即序化。
        if (!root)//如果当前节点为空，就用#来表示。
        {
            *str << "#,";
        }
        else
        {
            *str << root->value << ",";
            recursion1(root->left,str);
            recursion1(root->right, str);
        }
    }

    Node* deserialize(string data)
    {
        stringstream ss;
        vector<string> tokens;
        string token;
        ss << data;
        while (getline(ss, token, ','))
        {
            tokens.push_back(token);
        }

        cnt = 0;
        return recursion2(tokens);
    }

    int cnt;
    //设置成全局变量，记录当前数组消费到了哪里。
    //在其他地方都能影响到cnt，实现向量遍历。
    Node* recursion2(vector<string> strs)
    {
        if (cnt >= strs.size()) return NULL;
        string cur = strs[cnt++];
        if (cur == "#") return NULL;
        else
        {
            Node* treenode = new Node(stoi(cur));
            //然后去消费左右子树
            treenode->left = recursion2(strs);
            //因为recursion2是有返回值的，所以成功将节点连接，树得以搭建。
            treenode->right = recursion2(strs);
            return treenode;
        }
    }

    
};

int main()
{
    int arr[] = { 5,1,4,7,3,9,10,6,8,2 };
    int len = sizeof(arr) / sizeof(int);
    Node* root = create_tree(arr, len);

    Search bfs;
    string str = bfs.serialize(root);
    cout << str << endl;

    Node* newroot = bfs.deserialize(str);
    traverse(newroot);
    
    return 0;
}


Node* create_tree(int* arr, int len)
{
    Node* root = new Node(arr[0]);

    for (int i = 1; i < len; i++)
    {
        Node* current = root;
        Node* pre = root;
        while (current)
        {
            pre = current;
            if (arr[i] <= current->value)
            {
                current = current->left;
            }
            else
            {
                current = current->right;
            }
        }

        Node* newNode = new Node(arr[i]);
        if (arr[i] <= pre->value) pre->left = newNode;
        else pre->right = newNode;
    }

    return root;
}


void traverse(Node* root)
{
    if (!root)return;
    cout << root->value << " ";
    traverse(root->left);
    traverse(root->right);
}