绝对的NumPy基础教程

原文链接：NumPy: the absolute basics for beginners — NumPy v2.0 Manual

如何导入 numpy ?

import numpy as np

将 numpy 库以 np 的简写导入程序之中，之后库中的内容都用 np. 来进行引用

优点：区分于其他库中的同名内容

读本文的示例程序

>>> a = np.array([[1, 2, 3],
...				  [4, 5, 6]])
>>> a.shape
(2, 3)

>>> 和 ... 后面跟的行都是输入代码，注意 <<< 和 ... 不是代码实际内容

其他的行都是输出内容

为什么用 NumPy?

Python的列表承载的可以是异类元素，这使得它使用起来更灵活，但牺牲了部分效率。

NumPy 处理的是同类元素数组，它可以在 CPU 级别优化同类元素数组的计算，提供高速计算、低内存消耗、和高级语法。

什么是数组？

在计算机科学中，数组是用来存储和检索数据的结构。

我们通常用一些网格来表示数组，每个格子放一个元素，比如一个一维数组，就像一个列表：

一个二维数组就像一个表格：

一个三维数组就像一张张表格。一个四维数组就像一堆堆表格摞。

这个概念可以持续到 $n$ 维

所以 NumPy 的基本数据结构就是 $n$ 维数组 ndarray

NumPy 里的数组大都要满足一些共同条件，比如：

• 数组的所有元素必须是相同类型
• 一旦创建，数组的元素个数就不能改变
• 数组的形状必须是方形的，不能参差不齐。比如，一个二维数组的每一行都要有相同的列数。

一旦这些条件被满足，NumPy 就可以利用它们来进行高效存储和计算。

在下面的文章中，用数组代表 ndarray 的实例。

数组的基本操作

可以用 Python 的序列数据类型，比如 列表(list) 来创建数组 。

>>> a = np.array([1, 2, 3, 4, 5, 6])
>>> a
array([1, 2, 3, 4, 5, 6])

array 的元素可以用很多种方法来进行访问。比如，我们可以跟列表一样直接通过方括号来引用元素：

>>> a[0]
1

note : 第一个元素从下标 0 开始索引而不是 1

就像列表一样，数组元素的值可以被修改：

>>> a[0] = 10
>>> a
array([ 10, 2, 3, 4, 5, 6 ])

就像列表一样，可以对数组进行切片操作：

>>> a[:3]
array([10, 2, 3])

但有很大的一点不同：列表切片生成一个与原来列表无关的新列表副本(copy) , 而数组切片生成的只是原来数组的一个视图(view) , 它还是指向原来的数组 . 原来的数组还是可以通过视图来修改。

>>> b = a[3:]
>>> b
array([4, 5, 6])
>>> b[0] = 40	# 修改 view
>>> a
array([ 10, 2, 3, 40, 5, 6 ])

二维或更高维的数组可以用 Python 的嵌套序列来创建：

>>> a = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
>>> a
array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])

在 NumPy 里，一个数组的一个维度被称为轴( axis) . 这个名词用来区分数组的维度和数据的维度。

比如，一个数组 $3\times 4$ 的二维数组 a 可以存放 3 个 4 维点，但它只有两条轴。

另一个不同是，多维数组可以只用一个方括号来索引元素：

>>> a[1,3]
8

note: 行列索引一般作为最后两个索引

note: 在数学里，0 维数组被称为常数 (scalar) , 1 维数组被称为向量 (vector) , 2 维数组被称为矩阵 (matrix) , 更高维的数组被称为张量 (tensor) 。在 Numpy 里最好不要这么理解。比如，二维数组和矩阵的运算就存在着很多不同。在其他 Python 库如 PyTorch 里的基本数据结构被称为 tensor 。

数组的属性

本节主要介绍数组的维度(ndim) , 形状(shape) , 大小 (size) , 数据类型(dtype)

---

数组的维数储存在数组的 ndim 属性中

>>> a.ndim
2

$n$ 维数组的 shape 是一个 $n$ 元元祖 ，给出各维的大小

>>> a.shape
(3, 4)
>>> len(a.shape) == a.ndim  # ndim 等于 shape 的维数
True

数组存放的元素总数被称为数组的大小，存放在 size 属性中

>>> a.size
12
>>> import math
>>> a.size = math.prod(a.shape) # size 等于 shape 的乘积
True

数组的元素都是相同类型，用属性 dtype 来记录

>>> a.dtype
dtype('int64')  # 64 位整数 int

如何创建常用的数组

本节主要介绍 np.zeros() , np.ones() , np.empty() , np.arrange() , np.linspace()

---

创建元素全是 0 的数组：

>>> np.zeros(2)
array([0., 0.])

创建元素全是 1 的数组：

>>> np.ones(2)
array([1., 1.])

甚至可以创建元素为空的数组。当然并不是为空，只是没有人为给元素赋初值，只是拿了一堆内存里的未知垃圾值。这样的效率更高，但在之后要记得给它的元素赋有意义的新值，要不然程序可能会莫名其妙的。

>>> np.empty(2)
array([1.12542193e-311, 0.00000000e+000]) # 未知垃圾值，每次可能不一样

可以直接用一列元素来创建数组：

>>> np.arange(4)
array([0, 1, 2, 3])	# 从 0(默认) 到 4(不包括)

可以指定范围和步长：

>>> np.arange(2, 9, 2)
array([2, 4, 6, 8])		# 从 2 到 9 , 步长为 2

可以用关于索引的线性元素来创建数组。它的特征是元素之间间隔相同：

>>> np.linspace(0, 10, num = 5)
array([ 0. ,  2.5,  5. ,  7.5, 10. ])	# 0(包含) 到 10(包含) 之间 5 个间隔相同的元素

Numpy 的默认数据类型是 np.float64 , 即 64 位浮点数，可以用 dtype 关键字来指定元素类型

>>> x = np.ones(2, dtype=np.int64)
>>> x
array([1, 1], dtype=int64)

增、删、排序

本节主要介绍 np.sort()、np.concatenate()

---

数组排序的主要函数是 np.sort() , 你可以指定排序的轴 (axis)、方法(kind)、升逆序(order)等。

假设你现在有数组

>>> arr = np.array([2, 1, 5, 3, 7, 4, 6, 8])

可以直接用 np.sort() 将其元素按照升序排序，返回元素排序后的新数组：

>>> np.sort(arr)
array([1, 2, 3, 4, 5, 6, 7, 8])

除此之外，还有一些特定的排序函数：

• argsort：返回对应元素的序号数组

• lexsort：稳定的元组字典排序

• searchsorted：对已排序数组进行二分查找

• partition：部分排序

假设你现在有数组

>>> a = np.array([1, 2, 3, 4])
>>> b = np.array([5, 6, 7, 8])

可以用 np.concatenate() 把它们连接起来：

>>> np.concatenate((a, b))
array([1, 2, 3, 4, 5, 6, 7, 8])

假设你现在有数组

>>> x = np.array([[1, 2], [3, 4]])
>>> y = np.array([[5, 6]])

也可以在第一维度上把他们连接起来：

>>> np.concatenate((x, y), axis=0)
array([[1, 2],
       [3, 4],
       [5, 6]])

想删除数组的元素，你可以直接把想要留下来的元素通过切片表达出来。

如何获取数组的形状和大小

本节主要介绍 ndarray.ndim , ndarray.size 和 ndarray.shape

---

ndarray.ndim 告诉你数组轴的数量，也就是数组的维数

ndarray.size 告诉你数组一共有多少个元素

ndarray.shape 告诉你每根轴上有多少个元素。比如 $2\times 3$ 的二维数组的形状是 (2,3)

比如

>>> array_example = np.array([[[0, 1, 2, 3],
...                           [4, 5, 6, 7]],
...
...                           [[0, 1, 2, 3],
...                           [4, 5, 6, 7]],
...
...                          [[0 ,1 ,2, 3],
...                           [4, 5, 6, 7]]])

可以分别获取其维数、大小和形状

>>> array_example.ndim
3
>>> array_example.size
24
>>> array_example.shape
(3, 2, 4)

改变数组的形状

本节主要介绍 ndarray.reshape()

---

可以在不改变数组大小的情况下改变数组的形状。

比如你有

>>> a = np.arange(6)
>>> print(a)
[0 1 2 3 4 5]

可以用 reshape 来改变它的形状，比如 $2\times 3$ , $3\times 2$ :

>>> b = a.reshape(3, 2)
>>> print(b)
[[0 1]
 [2 3]
 [4 5]]
>>> c = a.reshape(2,3)
>>> print(c)
[[0 1 2]
 [3 4 5]]

也可以用 np.reshape() 函数，这样可以额外传入几个可选参数：

>>> np.reshape(a, newshape=(2, 3), order='C')
array([[0, 1, 2],
       [3, 4, 5]])
>>> np.reshape(a, newshape=(2, 3), order='F')
array([[0, 2, 4],
       [1, 3, 5]])

• a 是原数组
• newshape 是新形状，要和原来的形状适配
• order 是方法，主要有 3 种，C 方式是行主序，F (Fortran)方式是列主序，A 是自动根据内存分配方式

行主序：在内存中按照一行一行连续存储，因此元素分配从前往后是 (0,0) , (0,1) , (0,2) ,(1,0),(1,1),(1,2)

列主序：在内存中按照一列一列连续存储，因此元素分配从前往后是 (0,0) , (1,0) , (0,1) ,(1,1),(0,2),(1,2)

添加新轴

本文主要介绍 np.newaxis , np.expand_dims

---

可以用 np.newaxis , np.expand_dims 来拓展已有数组的维度，$n$ 维数组加上一根新轴变成 $n+1$ 维数组

比如，现在有

>>> a = np.array([1, 2, 3, 4, 5, 6])
>>> a.shape
(6,)

可以用np.newaxis 来加根新轴：

>>> a2 = a[np.newaxis, :]
>>> a2.shape
(1, 6)

根据 np.newaxis 的位置不同，可以在左方或右方添加维度

>>> a3 = a[: , np.newaxis]
>>> a3.shape
(6, 1)

也可以用 np.expand_dims 来指定新维度的插入位置：

>>> b = np.expand_dims(a, axis=1)
>>> b.shape
(6, 1)
>>> c = np.expand_dims(a, axis=1)
>>> c.shape
(1, 6)

索引和切片

你可以使用和 Python 列表一样的索引和切片方式

>>> data = np.array([1, 2, 3])
>>> data[1]
2
>>> data[0:2]
array([1, 2])
>>> data[1:]
array([2, 3])
>>> data[-2:]
array([2, 3])

可以这么理解：

有时候你想对数组的一些子数组进行计算，那切片就行。

有时候你还想提取出数组里一些满足特定条件的元素，这在 NumPy 里也是很简单的。

比如，你现在有

>>> a = np.array([[1 , 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])

你可以轻易地提取出小于 5 的元素：

>>> a[ a < 5 ]
array([1, 2, 3, 4])

只要在方框内写出你想要的元素满足的布尔性质就行：

>>> five_up = (a >= 5)
>>> a[ five_up ]
array([ 5, 6,  7,  8,  9, 10, 11, 12])

选中能被 2 整除的元素：

>>> divisible_by_2 = a[ a % 2 == 0 ]
>>> divisible_by_2
array([ 2,  4,  6,  8, 10, 12])

还可以对布尔表达式使用 & 和 | 来复合出更复杂的条件：

>>> c = a[(a > 2) & (a < 11)]
>>> c
array([ 3,  4,  5,  6,  7,  8,  9, 10])

数组的布尔运算返回对每个元素进行布尔运算得到的判断矩阵，而判断矩阵可以用被在方括号里对数组元素进行选择：

>>> a
array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])
>>> five_up = (a > 5) | (a == 5)
>>> five_up
array([[False, False, False, False],
       [ True,  True,  True,  True],
       [ True,  True,  True,  True]])
>>> a[ five_up ]
array([ 5, 6,  7,  8,  9, 10, 11, 12])

你还可以用 np.nonzero() 来获取数组中非零元素块的切片。在判断矩阵中，非零元素即 True .

>>> b = np.nonzero(a < 5)
>>> b
(array([0, 0, 0, 0], dtype=int64), array([0, 1, 2, 3], dtype=int64))

返回了一个元组，第一个元素代表第 1 维的索引，第二个元素代表第 2 维的索引

如果你想生成这些非零元素的完整索引，可以用 zip 把它们打包起来：

>>> list_of_coordinates= list(zip(b[0], b[1]))
>>> list_of_coordinates
[(0, 0), (0, 1), (0, 2), (0, 3)]

np.nonzero() 也可以用来选中元素：

>>> a[b]
array([1, 2, 3, 4])

如果满足条件的元素不存在，将返回空数组：

>>> not_there = np.nonzero(a == 42)
>>> not_there
(array([], dtype=int64), array([], dtype=int64))

从已有数据建立数组

本节主要介绍 np.vstack , np.hstack , np.hsplit , ndarray.view() , ndarray.copy

---

可以从已有的数组开始创建新的数组。

假设我们现在有

>>> a = np.array([1,  2,  3,  4,  5,  6,  7,  8,  9, 10])

可以通过切片来得到一个子数组：

>>> arr1 = a[3:8]
>>> arr1
array([4, 5, 6, 7, 8])

也可以通过堆积两个已有数组来创建新的数组，无论是横向拼接还是纵向拼接。

假设你现在有数组 a1 和 a2 ：

>>> a1 = np.array([[1, 1],
               [2, 2]])
>>> a2 = np.array([[3, 3],
               [4, 4]])

通过 vstack() 把它们进行纵向拼接：

np.vstack((a1, a2))
array([[1, 1],
       [2, 2],
       [3, 3],
       [4, 4]])

通过 vstack() 把它们进行横向拼接：

>>> np.hstack((a1, a2))
array([[1, 1, 3, 3],
       [2, 2, 4, 4]])

反之，可以通过 hsplit() 对数组进行纵向分割。

比如，假设你现在有

>>> x = np.arange(1, 25).reshape(2, 12)
>>> x
array([[ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12],
       [13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24]])

如果你想把它横向分割为三个相同形状的数组，你可以这么写代码：

>>> np.hsplit(x, 3)
[array([[ 1,  2,  3,  4],
         [13, 14, 15, 16]]), array([[ 5,  6,  7,  8],
         [17, 18, 19, 20]]), array([[ 9, 10, 11, 12],
         [21, 22, 23, 24]])]

如果你想从第 2 列和第 6 列处将它横向分割为三个数组，你可以这么写代码：

>>> p.hsplit(x,(2,6))
[array([[ 1,  2],
        [13, 14]]),
 array([[ 3,  4,  5,  6],
        [15, 16, 17, 18]]),
 array([[ 7,  8,  9, 10, 11, 12],
        [19, 20, 21, 22, 23, 24]])]

你可以通过 view() 方法来创建数组的一个视图分身，它和原数组操作内存中的同一片数据，就像影子一样。这样可以节省空间，但注意不能随便修改视图，因为会影响原数组。

假设你创建了数组：

>>> a = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])

现在我们通过切片来获取 a 的一个视图 b1 . 修改 b1 导致 a 也跟着变：

>>> b1 = a[0, :]
>>> b1
array([1, 2, 3, 4])
>>> b1[0] = 99
>>> b1
array([99,  2,  3,  4])
>>> a
array([[99,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])

通过 copy() 方法可以获取数组的深层次拷贝，这个新数组与原数组在内存中毫无联系：

>>> b2 = a[0, :].copy()
>>> b2
array([99, 2, 3, 4])
>>> b2[0] = 1
>>> b2
array([1,  2,  3,  4])
>>> a
array([[ 99,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])

基本的数组运算

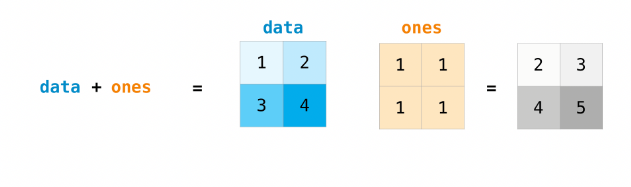
假设你有两个数组 data 和 ones :

>>> data = np.array([1, 2])
>>> ones = np.ones(2, dtype=int)

可以直接将两个相同形状的数组相加，这使得对应元素相加：

>>> data + ones
array([2, 3])

除了加法，减法、乘法、除法也是一样的道理。

>>> data - ones
array([0, 1])
>>> data * data
array([1, 4])
>>> data / data
array([1., 1.])

如果你想求所有元素的和，直接用 sum() 方法就行：

>>> a = np.array([1, 2, 3, 4])
>>> a.sum()
10

对 2 维数组按行求和或者按列求和，就要指定运算的轴了。

假设有数组：

>>> b = np.array([[1, 2], [3, 4], [5, 6]])

按行求和：

>>> b.sum(axis=0)
array([ 9, 12])

按列求和：

>>> b.sum(axis=1)
array([ 3,  7, 11])

广播机制

有时候你想把两个不同形状的数组进行基本运算。比如用一个数来乘上一个数组，想达到数组的每个元素都乘这个数的结果。

在运算过程中，NumPy 会帮你把参与运算的数组变为相同形状，这称为广播机制：

>>> data = np.array([1.0, 2.0])
>>> data * 1.6
array([1.6, 3.2])

广播机制不能万能的，当两个数组的形状不能适配时（相同轴上大小不等，且都不是1），就会报 ValueError 的错误。

更多有用的运算

NumPy 还提供了很多聚合方法。

• max() 计算最大值
• min() 计算最小值
• sum() 计算元素和
• mean() 计算元素均值
• prod 计算元素乘积
• std 计算元素标准差

>>> data.max()
2.0
>>> data.min()
1.0
>>> data.sum()
3.0

现在创建一个新数组 a ：

>>> a = np.array([[0.45053314, 0.17296777, 0.34376245, 0.5510652],
...              [0.54627315, 0.05093587, 0.40067661, 0.55645993],
...              [0.12697628, 0.82485143, 0.26590556, 0.56917101]])

默认情况下，聚合方法的返回结果都是对整个数组进行计算的：

>>> a.sum()
4.8595784
>>> a.min()
0.05093587

你可以指定运算的轴，比如，想知道每一列的最大数，可以运行：

>>> a.min(axis=0)
array([0.12697628, 0.05093587, 0.26590556, 0.5510652 ])

运算的轴会消失 。

创建矩阵

可以通过传入两层嵌套列表来生成二维数组(或者称为矩阵)：

>>> data = np.array([[1, 2], [3, 4], [5, 6]])
>>> data
array([[1, 2],
       [3, 4],
       [5, 6]])

在处理矩阵时，切片是个十分便捷的操作：

>>> data[0, 1]
2
>>> data[1:3]
array([[3, 4],
       [5, 6]])
>>> data[0:2, 0]
array([1, 3])

像一维数组(向量)一样，可以对矩阵进行聚合运算。

>>> data.max()
6
>>> data.min()
1
>>> data.sum()
21

矩阵的聚合运算可以在更小的维度内进行：

>>> data = np.array([[1, 2], [5, 3], [4, 6]])
>>> data
array([[1, 2],
       [5, 3],
       [4, 6]])
>>> data.max(axis=0)
array([5, 6])
>>> data.max(axis=1)
array([2, 5, 6])

只要矩阵形状相同，就可以直接进行对应元素的加减乘除运算：

>>> data = np.array([[1, 2], [3, 4]])
>>> ones = np.array([[1, 1], [1, 1]])
>>> data + ones
array([[2, 3],
       [4, 5]])

你也可以对不同形状的矩阵进行对应元素算术运算，只要其中之一是个行向量或列向量。NumPy 会自动执行广播机制。

>>> data = np.array([[1, 2], [3, 4], [5, 6]])
>>> ones_row = np.array([[1, 1]])
>>> data + ones_row
array([[2, 3],
       [4, 5],
       [6, 7]])

形状元组从左往右看，对应的维度更深。

>>> np.ones((4, 3, 2))
array([[[1., 1.],
        [1., 1.],
        [1., 1.]],

       [[1., 1.],
        [1., 1.],
        [1., 1.]],

       [[1., 1.],
        [1., 1.],
        [1., 1.]],

       [[1., 1.],
        [1., 1.],
        [1., 1.]]])

有很多方法来初始化一个给定形状的数组，比如 np.ones() 和 np.zeros() 以及 random.Generator 类

>>> np.ones(3)
array([1., 1., 1.])
>>> np.zeros(3)
array([0., 0., 0.])
>>> rng = np.random.default_rng() # 最简单的随机数生成器
>>> rng.random(3) 
array([0.63696169, 0.26978671, 0.04097352])

也可以在初始化时用元组给定数组的形状：

>>> np.ones((3, 2))
array([[1., 1.],
       [1., 1.],
       [1., 1.]])
>>> np.zeros((3, 2))
array([[0., 0.],
       [0., 0.],
       [0., 0.]])
>>> rng.random((3, 2)) 
array([[0.01652764, 0.81327024],
       [0.91275558, 0.60663578],
       [0.72949656, 0.54362499]])	# 可能不同

生成随机数

在很多应用场景里，需要生成随机数（伪随机数）。

可以使用 Generator.intergers() 来随机生成给定区间的整数。默认不包括区间右顶点，可以通过设置 endpoint=True 来修改。

>>> rng.integers(5, size=(2, 4))  # 2*4 的 0-5 之间的随机整数
array([[2, 1, 1, 0],
       [0, 0, 0, 4]])

获取唯一元素和元素计数

本节主要介绍 np.unique()

---

先准备好数组：

>>> a = np.array([11, 11, 12, 13, 14, 15, 16, 17, 12, 13, 11, 14, 18, 19, 20])

可以用 np.unique() 来获取数组中只出现一次的元素

>>> unique_values = np.unique(a)
array([11, 12, 13, 14, 15, 16, 17, 18, 19, 20])

加上参数 return_index=True 可以得到每一个元素第一次出现的索引：

>>> unique_values, indices_list = np.unique(a, return_index=True)
>>> indices_list
array([ 0,  2,  3,  4,  5,  6,  7, 12, 13, 14]

加上参数 return_counts 可以得到每一个元素出现的次数：

>>> unique_values, occurrence_count = np.unique(a, return_counts=True)
>>> occurrence_count
array([3, 2, 2, 2, 1, 1, 1, 1, 1, 1], dtype=int64)

对二维数组也同样适用：

>>> a_2d = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [1, 2, 3, 4]])
>>> unique_values = np.unique(a_2d)
array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12])

可以加上操作的轴序号：

>>> unique_rows = np.unique(a_2d, axis=0)	# 不同行
array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])

也可以传入 return_counts=True 和 return_index=True 等参数

>>> unique_rows, indices, occurrence_count = np.unique(
     a_2d, axis=0, return_counts=True, return_index=True)
>>> unique_rows, indices, occurrence_count
(array([[ 1,  2,  3,  4],
        [ 5,  6,  7,  8],
        [ 9, 10, 11, 12]]),
 array([0, 1, 2], dtype=int64),
 array([2, 1, 1], dtype=int64))

转置和重塑矩阵

本节主要介绍 ndarray.reshape() ， ndarray.transpose() , ndarray.T

矩阵的转置是很常见的，属性 ndarray.T 可以得到转置后的新矩阵。转置后的数组的形状从左往右整个翻转过来。

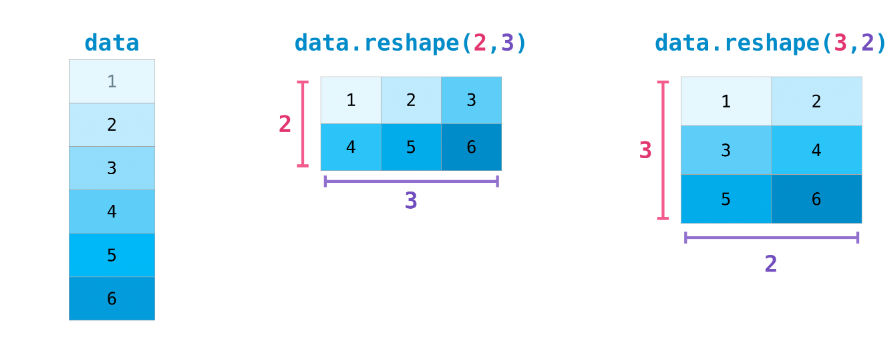
改变矩阵的形状也是一件很常见的事。直接向 ndarray.reshape() 传递改变后的形状元组即可。

>>> data.reshape(2, 3)
array([[1, 2, 3],
       [4, 5, 6]])
>>> data.reshape(3, 2)
array([[1, 2],
       [3, 4],
       [5, 6]])

ndarray.transpose() 方法是 ndarray.T 的进阶版。

如何翻转数组

本节主要介绍 np.flip()

---

向 np.flip() 传递想要翻转的数组和轴，就可以在指定轴上翻转数组。

翻转一维数组

>>> arr = np.array([1, 2, 3, 4, 5, 6, 7, 8])
>>> reversed_arr = np.flip(arr)
array([8, 7, 6, 5, 4, 3, 2, 1])

翻转二维数组

>>> arr_2d = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
>>> reversed_arr = np.flip(arr_2d)
>>> reversed_arr
array([[12, 11, 10,  9],
       [ 8,  7,  6,  5],
       [ 4,  3,  2,  1]])

可以翻转每一列：

>>> reversed_arr_rows = np.flip(arr_2d, axis=0)
array([[ 9, 10, 11, 12],
       [ 5,  6,  7,  8],
       [ 1,  2,  3,  4]])

可以翻转每一行：

>>> reversed_arr_columns = np.flip(arr_2d, axis=1)
array([[ 4,  3,  2,  1],
       [ 8,  7,  6,  5],
       [12, 11, 10,  9]])

可以翻转某一行：

>>> arr_2d[1] = np.flip(arr_2d[1])
>>> arr_2d[1]
array([[ 1,  2,  3,  4],
       [ 8,  7,  6,  5],
       [ 9, 10, 11, 12]])

可以翻转某一列：

>>> arr_2d[:,1] = np.flip(arr_2d[:,1])
>>> arr_2d
array([[ 1, 10,  3,  4],
       [ 8,  7,  6,  5],
       [ 9,  2, 11, 12]])

重塑和压平多元数组

本节主要介绍 ndarray.flatten() 和 ndarray.ravel()

---

压平一个数组有两种常用方法 flatten() 和 ravel() . 两个方法最大的不同点是 ravel()返回的是个 view .

如果你有数组：

>>> x = np.array([[1 , 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])

可以用 flatten() 来将数组压平为一维数组：

>>> x.flatten()
array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12])

改变 flatten() 返回的新数组不会影响原数组：

>>> a1 = x.flatten()
>>> a1[0] = 99
>>> print(x) 
[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]]
>>> print(a1)
[99  2  3  4  5  6  7  8  9 10 11 12]

当你使用 ravel() 时，改变返回的数组会影响原数组：

>>> a2 = x.ravel()
>>> a2[0] = 98
>>> print(x)
[[98  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]]
>>> print(a2) 
[98  2  3  4  5  6  7  8  9 10 11 12]

如何获得帮助文档

本节主要介绍 help() , ? , ??

---

当提到数据科学时，无法避免提到 Python 和 NumPy 。 依托于 Python , NumPy 有一套很好的帮助系统。每个函数或方法都对应一个注释字符串，它简明扼要地阐述了函数的用法。使用 help() 能够迅速获得一个函数的注释字符串。例如：

>>> help(max)
Help on built-in function max in module builtins:

max(...)
    max(iterable, *[, default=obj, key=func]) -> value
    max(arg1, arg2, *args, *[, key=func]) -> value
    
    With a single iterable argument, return its biggest item. The
    default keyword-only argument specifies an object to return if
    the provided iterable is empty.
    With two or more arguments, return the largest argument.

在 IPython系统中，还增加了 ? 关键字。例如：

In [0]: max?
max(iterable, *[, default=obj, key=func]) -> value
max(arg1, arg2, *args, *[, key=func]) -> value

With a single iterable argument, return its biggest item. The
default keyword-only argument specifies an object to return if
the provided iterable is empty.
With two or more arguments, return the largest argument.
Type:      builtin_function_or_method

这些方法也可以查看类注释和对象。

例如：

a = np.array([1, 2, 3, 4, 5, 6])

你可以在交互式窗口中输入：

In [1]: a?
Type:            ndarray
String form:     [1 2 3 4 5 6]
Length:          6
File:            ~/anaconda3/lib/python3.9/site-packages/numpy/__init__.py
Docstring:       <no docstring>
Class docstring:
ndarray(shape, dtype=float, buffer=None, offset=0,
        strides=None, order=None)

An array object represents a multidimensional, homogeneous array
of fixed-size items.  An associated data-type object describes the
format of each element in the array (its byte-order, how many bytes it
occupies in memory, whether it is an integer, a floating point number,
or something else, etc.)

Arrays should be constructed using `array`, `zeros` or `empty` (refer
to the See Also section below).  The parameters given here refer to
a low-level method (`ndarray(...)`) for instantiating an array.

For more information, refer to the `numpy` module and examine the
methods and attributes of an array.

Parameters
----------
(for the __new__ method; see Notes below)

shape : tuple of ints
        Shape of created array.
...

这也适用于你自己创建的函数，只要在定义时加上三引号注释："""注释内容"""，比如：

def double(a):
  '''Return a * 2'''
  return a * 2

可以获得信息：

In [2]: double?
Signature: double(a)
Docstring: Return a * 2
File:      ~/Desktop/<ipython-input-23-b5adf20be596>
Type:      function

想要看源代码，只需要在交互式窗口中输入 ?? :

In [3]: double??
Signature: double(a)
Source:
def double(a):
    '''Return a * 2'''
    return a * 2
File:      ~/Desktop/<ipython-input-23-b5adf20be596>
Type:      function

如果询问的对象是由其他语言编译而成的，? 和 ?? 将返回一样的简介内容，不会有源代码。这在 Python 语言的内置函数中很常见。

和数学公式打交道

能够简单地输入数学公式是 NumPy 很受欢迎的的原因之一。比如，平方误差函数：

只需翻译为：

很强的一点是，上面的 predictions 和 labels 可以包含成千上万个元素，只要形状一样就行。

你可以这么理解：

怎样保存和加载 NumPy 对象

本节包含 np.save , np.savez ,np.savetxt , np.load , np.loadtxt

---

有时候你可能想把你的数组存入磁盘而不用再一次运行代码就能得到。NumPy 中有很多方法可以做到这一点。loadtxt() 和 savetxt() 用来把数组存入 .txt 文件和从 .txt 文件中读取数组。load() 和 save() 用来把数组存入 .npy 二进制文件和从 .npy 二进制文件中读取数组。savez() 用于将数组存入 .npz 文件。

.npy 和 .npz 文件可以用来存储数据，形状，和其他对象。它们可以跨平台访问。

如果想把数组存到单独的一个文件之中，用 save() 保存到 .npy 文件之中。如果想在一个文件中保存多个数组，可以用 savez() 保存到 .npz 文件之中。还可以用 savez_compressed() 来压缩数据，保存到 .npz 文件中。

最简单的方法就是给 np.save() 传递需要保存的对象和要保存到的文件名。

>>> a = np.array([1, 2, 3, 4, 5, 6])
>>> np.save('filename', a)

用 np.load() 来重新加载数组：

>>> b = np.load('filename.npy')
>>> print(b)
[1 2 3 4 5 6]

可以用 savetxt() 来将数组存入 .txt 或 .csv 文件之中。用 loadtxt() 来重新加载数组。

例如：

>>> csv_arr = np.array([1, 2, 3, 4, 5, 6, 7, 8])
>>> np.savetxt('new_file.csv', csv_arr)
>>> np.loadtxt('new_file.csv')
array([1., 2., 3., 4., 5., 6., 7., 8.])

在处理 .csv 或 .txt 文件时，可以指定各种参数，如 header, footer, delimiter 等。与之相比，.npy 文件和 .npz 文件更小也更易读。

如果想操作更加复杂的 .txt 文件，可以去学习一下 genfromtxt() 函数。

导入导出 CSV 文件

CSV 文件非常简便易读。操作 CSV 文件就不得不提到另一个第三方科学计算库 Pandas 。

>>> import pandas as pd
# 假设文件中每一列数据都具有相同的类型
>>> x = pd.read_csv('music.csv', header=0).values
>>> print(x)
[['Billie Holiday' 'Jazz' 1300000 27000000]
 ['Jimmie Hendrix' 'Rock' 2700000 70000000]
 ['Miles Davis' 'Jazz' 1500000 48000000]
 ['SIA' 'Pop' 2000000 74000000]]

# 可以选择导入的列
>>> x = pd.read_csv('music.csv', usecols=['Artist', 'Plays']).values
>>> print(x)
[['Billie Holiday' 27000000]
 ['Jimmie Hendrix' 70000000]
 ['Miles Davis' 48000000]
 ['SIA' 74000000]]

用 Pandas 也可以很方便地导出数据。你需要用数组创建一个数据框( dataframe ) , 然后借助数据框来导出数据：

>>> a = np.array([[-2.58289208,  0.43014843, -1.24082018, 1.59572603],
...              [ 0.99027828, 1.17150989,  0.94125714, -0.14692469],
...              [ 0.76989341,  0.81299683, -0.95068423, 0.11769564],
...              [ 0.20484034,  0.34784527,  1.96979195, 0.51992837]])
>>> df = pd.DataFrame(a)	# 创建数据框
>>> print(df)
          0         1         2         3
0 -2.582892  0.430148 -1.240820  1.595726
1  0.990278  1.171510  0.941257 -0.146925
2  0.769893  0.812997 -0.950684  0.117696
3  0.204840  0.347845  1.969792  0.519928
>>> data = pd.read_csv('pd.csv')

>>> df.to_csv('pd.csv')  # 导出到 csv 文件中
>>> data = pd.read_csv('pd.csv')  # 导入

也可以用 NumPy 的 savetxt() :

>>> np.savetxt('np.csv', a, fmt='%.2f', delimiter=',', header='1,  2,  3,  4')

使用命令行查看：

$ cat np.csv
#  1,  2,  3,  4
-2.58,0.43,-1.24,1.60
0.99,1.17,0.94,-0.15
0.77,0.81,-0.95,0.12
0.20,0.35,1.97,0.52

使用 Matplotlib 绘制数组

如果想可视化你的数据，可以使用 Matplotlib 库

例如：

>>> a = np.array([2, 1, 5, 7, 4, 6, 8, 14, 10, 9, 18, 20, 22])
>>> import matplotlib.pyplot as plt    # 导入 matplotlib.pyplot
# 如果使用的是 jupyter notebook , 加上
# % matplotlib inline 来展示图像
>>> plt.plot(a)
# 如果是命令行环境，加上
# plt.show() 来展示图像

可以这样可视化一维数组：

>>> x = np.linspace(0, 5, 20)
>>> y = np.linspace(0, 10, 20)
>>> plt.plot(x, y, 'purple')  # 画线
>>> plt.plot(x, y, 'o')   # 画点

借助 Matplotlib , 你可以自定义很多绘图设置：

>>> fig = plt.figure()
>>> ax = fig.add_subplot(projection='3d')
>>> X = np.arange(-5, 5, 0.15)
>>> Y = np.arange(-5, 5, 0.15)
>>> X, Y = np.meshgrid(X, Y)
>>> R = np.sqrt(X**2 + Y**2)
>>> Z = np.sin(R)
>>> ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='viridis')