运算放大器应用——滤波器

运放滤波电路是利用运算放大器（运放）的高增益、高输入阻抗和低输出阻抗等特性，结合电容、电阻等无源元件构成的滤波电路，能实现对特定频率信号的选择通过或抑制。下面从其原理、类型以及应用场景进行介绍：

原理

运放滤波电路主要基于 RC（电阻 - 电容）滤波原理，并借助运放增强性能。在 RC 滤波电路中，电容对不同频率的信号呈现不同的容抗（XC=2πfC1 ，其中 f 是信号频率，C 是电容值），频率越高，容抗越小；电阻的阻值不随频率变化。通过合理配置电阻和电容的参数，就能让电路对不同频率的信号产生不同的响应。
运放接入电路后，能起到以下作用：

 

• 提高带负载能力：运放的低输出阻抗特性，使得滤波电路在连接负载后，输出电压不易受负载变化的影响，保证滤波效果的稳定性。
• 提升增益：可以根据需求设置运放的增益，对滤波后的信号进行放大，满足后级电路对信号幅度的要求。
• 隔离前后级电路：高输入阻抗特性使运放能够减少前级电路的负载效应，避免后级电路对前级电路的干扰，保证各级电路独立稳定工作。

类型

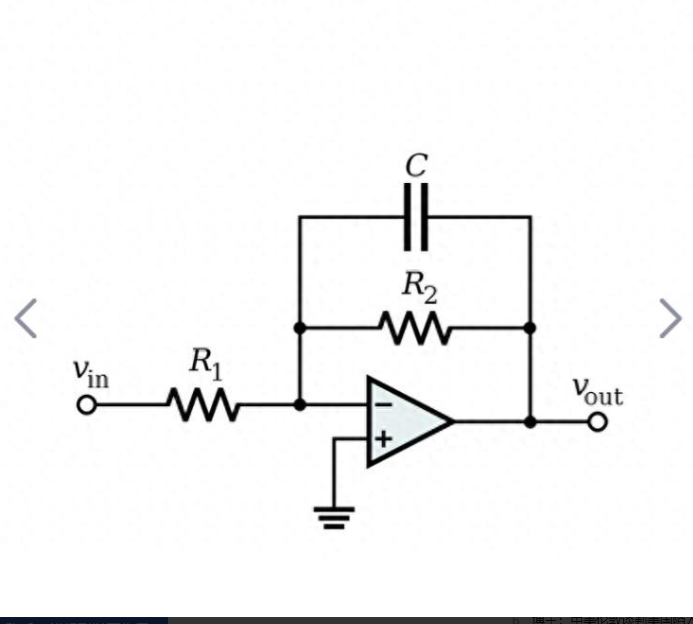
• 低通滤波器（LPF）：允许低频信号通过，抑制高频信号。典型的一阶有源低通滤波器由一个电阻、一个电容和一个运放组成，信号从电阻输入，电容连接在运放的输出端与反相输入端之间。随着信号频率升高，电容容抗减小，更多信号通过电容反馈到反相输入端，使输出信号幅度逐渐减小。二阶或高阶低通滤波器能实现更陡峭的过渡带，更有效地抑制高频信号。
• 高通滤波器（HPF）：与低通滤波器相反，允许高频信号通过，抑制低频信号。一阶有源高通滤波器中，电容与电阻的位置和低通滤波器中相反，信号从电容输入，电阻连接在运放的输出端与反相输入端之间。当信号频率降低时，电容容抗增大，信号衰减加剧，从而实现高通滤波功能。
• 带通滤波器（BPF）：只允许特定频率范围内的信号通过，抑制该范围之外的信号。一般由低通滤波器和高通滤波器组合而成，低通滤波器的截止频率高于高通滤波器的截止频率，两者之间的频率范围即为通带。
• 带阻滤波器（BEF，又称陷波滤波器）：抑制特定频率范围内的信号，让该范围之外的信号通过。常见的是基于双 T 网络的有源带阻滤波器，通过调整双 T 网络的参数以及运放的反馈电阻，实现对特定频率信号的有效抑制。

应用

• 音频处理：低通滤波：用于去除音频信号中的高频噪声，比如在音响系统中，滤除超出音频范围（一般认为 20Hz - 20kHz ）的高频干扰，使声音更加纯净。高通滤波：去除音频信号中的低频噪声，如交流电源产生的 50Hz 或 60Hz 工频干扰，同时还能避免低频信号对扬声器的过度驱动，保护扬声器。带通滤波：在均衡器中，通过设置不同频段的带通滤波器，对不同频率范围的声音信号进行提升或衰减，以满足不同的音效需求。
• 传感器信号处理：传感器输出的信号往往夹杂着各种噪声。例如，温度传感器输出的微弱电信号可能会受到周围电磁环境的干扰，通过低通滤波器可以滤除高频噪声，得到更准确的温度信号；应变片传感器输出的信号中可能存在低频的机械振动干扰，使用高通滤波器可去除低频噪声，提取有用的应变信号。
• 电源电路：在开关电源的输出端，会存在高频开关噪声，使用低通滤波器可以滤除这些高频噪声，使输出的直流电压更加稳定，为后级电路提供纯净的电源。
• 通信系统：在无线通信中，带通滤波器用于从众多频率的信号中选取特定频段的信号进行处理，滤除其他频段的干扰信号；带阻滤波器则可用于抑制特定频率的干扰信号，如在 GSM 通信系统中，抑制与工作频段相近的干扰信号，保证通信质量。