运算放大器的四种负反馈方式

运算放大器的负反馈根据取样方式（从输出端取样的方式）和比较方式（反馈信号与输入信号在输入端的比较方式 ）的不同，可分为四种基本类型：电压串联负反馈、电压并联负反馈、电流串联负反馈、电流并联负反馈。以下为你详细介绍：

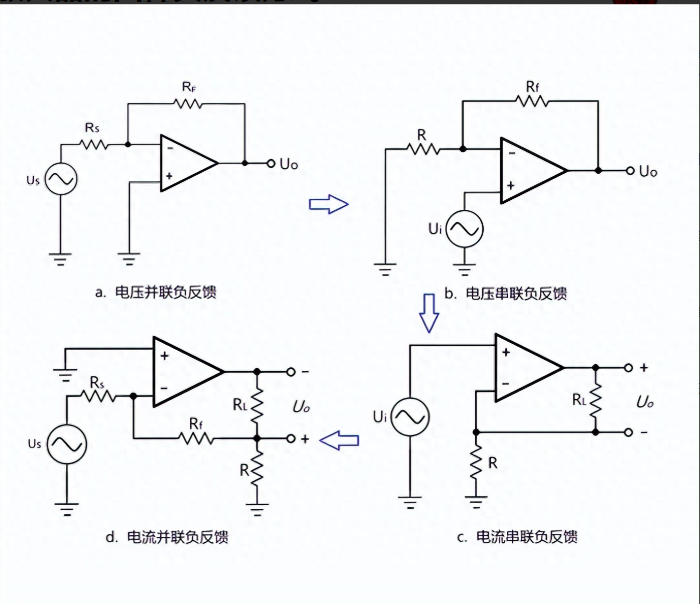
电压串联负反馈

• 电路结构特点：在输出端，反馈网络从输出电压取样，即反馈信号与输出电压成正比；在输入端，反馈电压与输入电压以串联的方式进行比较，也就是净输入电压Vid=Vi−Vf（Vi为输入电压，Vf为反馈电压 ）。常见的同相比例运算电路就是典型的电压串联负反馈电路，运算放大器的同相输入端接输入信号，反相输入端通过电阻网络连接到输出端构成反馈回路。
• 主要性能影响：输入电阻：由于反馈电压与输入电压串联，使得输入电流减小，根据输入电阻Rin=IiVi，在输入电压不变的情况下，输入电流减小，输入电阻增大，一般可达兆欧级别，能很好地减轻信号源的负载。输出电阻：输出电压趋于稳定，相当于输出电阻减小，使运算放大器的输出更接近理想电压源，带负载能力增强，当负载电阻变化时，输出电压基本保持不变。电压增益：闭环电压增益Avf=ViVo=1+R1Rf（Rf为反馈电阻，R1为反相输入端接地的电阻 ），增益主要由反馈网络的电阻决定，稳定性高。

电压并联负反馈

• 电路结构特点：输出端，反馈网络对输出电压进行取样，反馈信号与输出电压成正比；输入端，反馈电流与输入电流以并联的方式进行比较，净输入电流Iid=Ii−If（Ii为输入电流，If为反馈电流 ）。反相比例运算电路是典型的电压并联负反馈电路，输入信号通过电阻接运算放大器的反相输入端，同相输入端接地，输出端通过反馈电阻连接到反相输入端。
• 主要性能影响：输入电阻：反馈电流与输入电流并联，使得输入电流增大，输入电阻减小，一般在几十到几百欧的范围。输出电阻：输出电压趋于稳定，输出电阻减小，增强了带负载能力。电压增益：闭环电压增益Avf=ViVo=−R1Rf，负号表示输出与输入反相，增益稳定性好。

电流串联负反馈

• 电路结构特点：输出端，反馈网络对输出电流进行取样，反馈信号与输出电流成正比；输入端，反馈电压与输入电压以串联的方式进行比较，净输入电压Vid=Vi−Vf 。在一些需要对电流信号进行精确控制或转换的电路中会用到，比如将电流信号转换为电压信号的电路。
• 主要性能影响：输入电阻：反馈电压与输入电压串联，使得输入电流减小，输入电阻增大，有利于从信号源获取电压信号。输出电阻：输出电流趋于稳定，相当于输出电阻增大，使运算放大器的输出更接近理想电流源，当负载电阻变化时，输出电流基本保持恒定。互导增益：闭环互导增益Agf=ViIo较为稳定，能实现输入电压对输出电流的稳定控制。

电流并联负反馈

• 电路结构特点：输出端，反馈网络对输出电流进行取样，反馈信号与输出电流成正比；输入端，反馈电流与输入电流以并联的方式进行比较，净输入电流Iid=Ii−If 。常用于需要稳定输出电流，并且对输入电阻要求较低的场合。
• 主要性能影响：输入电阻：反馈电流与输入电流并联，使得输入电流增大，输入电阻减小。输出电阻：输出电流趋于稳定，输出电阻增大，增强了输出电流的恒流特性。互阻增益：闭环互阻增益Arf=IiVo较为稳定，能实现输入电流对输出电压的稳定控制。

 

这四种负反馈类型各有特点，在实际应用中，根据具体的电路需求，如对输入输出电阻的要求、需要稳定的是电压还是电流、期望的增益形式等，来选择合适的负反馈类型，以达到最佳的电路性能。