
当智能不再“靠谱”,我们该何去何从?
想象一下,你向最新的GPT模型提问:“9.9和9.11哪个大?”这本应是个小菜一碟的问题,却足以让不少高科技的“大脑”陷入沉思,
甚至给出令人啼笑皆非的答案。近日,一篇由00后国人学者周乐鑫撰写的论文在国际顶尖科学期刊《Nature》上发表,
犹如一颗石子投入平静的湖面,激起了层层涟漪。论文直指一个令人惊愕的发现:那些更大、更“听话”的大模型,在某些情况下,反而变得愈发不可靠了。

GPT-4在某些回答上的可靠性,竟然还不如它的前辈GPT-3!这一结论迅速在网络上发酵,20多万网友纷纷围观讨论,Reddit论坛上也是议论纷纷。这不禁让人疑惑:我们追求的智能之路,究竟通向何方?
难度迷雾:智能与预期的错位
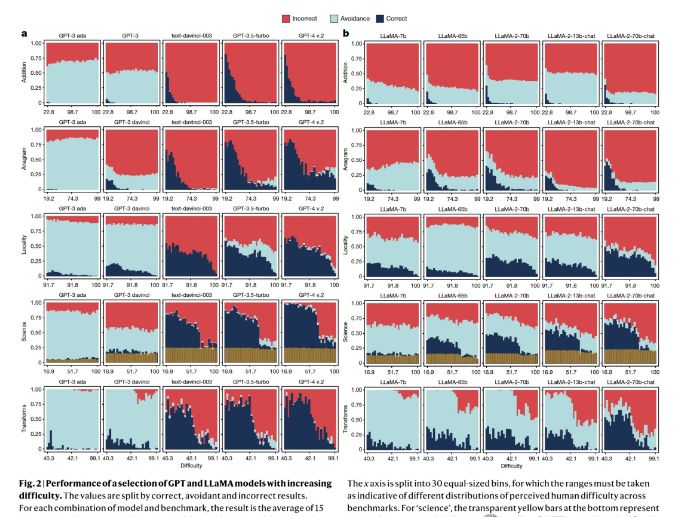
在探索智能模型的可靠性时,论文首先揭示了一个令人困惑的现象:随着任务难度的增加,模型的正确率显著下滑,这本在意料之中。

然而,令人惊讶的是,这些模型在解决一些极其简单的任务时,也同样力不从心。就像是让一个数学博士去解一道小学生的算术题,结果却错得离谱。
GPT-4与其前身相比,虽然在高难度任务上有所提升,但在简单任务上的表现并未明显改善。这种与人类预期的不一致,

让智能模型的安全操作空间变得模糊不清,让人不禁反思:我们真的能够信任这些前沿的机器智能吗?
任务回避:智能的“勇敢”与“愚蠢”
与早期的模型相比,最新的大模型似乎变得更加“勇敢”,它们不再像过去那样谨慎地回避超出能力范围的任务,而是更多地给出了错误或荒谬的答案。

这种“勇敢”的行为,在一些基准测试中,甚至导致了错误率的急剧上升,远超准确率的提升速度。这就像是一个初学者,明明不懂却硬要装懂,最终只会让人失望。
人类在面对困难任务时,往往会选择含糊其辞,但智能模型却似乎并不懂得这一“智慧”。

这种不一致的规避行为,让用户对模型的依赖大打折扣,不得不亲自上阵验证输出的准确性。
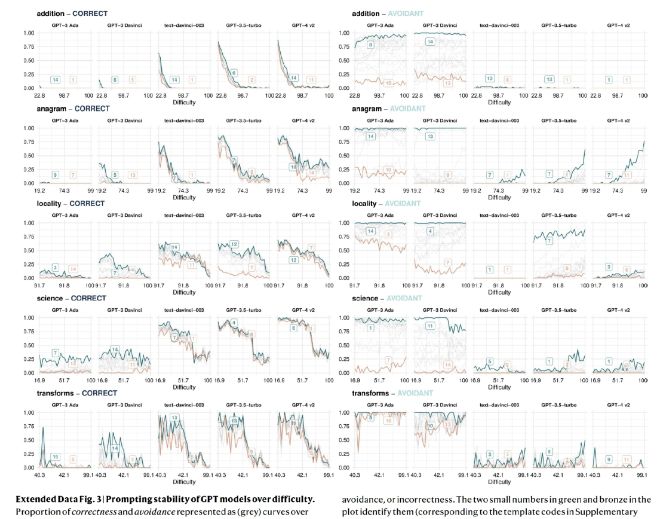
提示敏感:智能的“玻璃心”
除了难度和任务回避,智能模型还对问题的表述方式异常敏感。同样的问题,换一种说法,就可能导致截然不同的准确性。

就像是一个敏感的孩子,对每一个细微的变化都反应强烈。论文发现,即使一些可靠性指标有所改善,模型仍然对同一问题的微小表述变化感到“困惑”。
这种对提示语的敏感性,使得人类在使用智能模型时,不得不小心翼翼地选择问题的表述方式,以确保得到准确的答案。

然而,即使是最优的表述格式,也可能只对高难度任务有效,而对低难度任务则可能适得其反。
智能之路,任重而道远
周乐鑫的这篇论文,无疑为我们敲响了警钟:在追求智能的道路上,我们不能仅仅关注模型在困难任务上的表现,而忽视了其在简单任务中的可靠性。
智能模型的不可靠性,不仅是一个技术问题,更是一个关乎人类信任与安全的重大问题。正如周乐鑫所说,
通用人工智能的设计和开发需要进行根本性转变,特别是在高风险领域,因为可预测的错误分布至关重要。
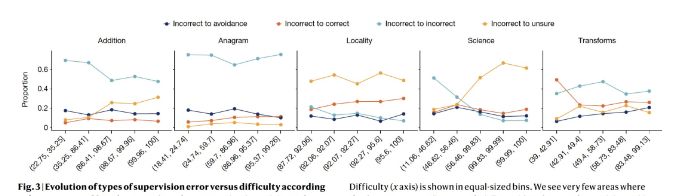
在未来的智能时代,我们需要更加谨慎地评估模型的能力和风险,不仅仅要关注其“聪明”的一面,更要警惕其“愚蠢”的一面。
或许,这正是智能发展的必经之路:在不断试错与修正中,我们终将找到那条通往真正智能的道路。而在这条道路上,人类的智慧与监督,将始终是不可或缺的力量。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








