T582309 图论-拓扑排序-最长路，没有难度，一命速通

题目传送门

题目描述

设 G 为有 n 个顶点的带权有向无环图，G 中各顶点的编号为 1 到 n，请设计算法，计算图 G 中 1,n 间的最长路径。

输入格式

输入的第一行有两个整数，分别代表图的点数 n 和边数 m。

第 2 到第 (m+1) 行，每行 3 个整数 u,v,w（u<v），代表存在一条从 u 到 v 边权为 w 的边。

输出格式

输出一行一个整数，代表 1 到 n 的最长路。

若 1 无法到达 n，请输出 −1。

输入输出样例

输入样例#1
2 1
1 2 1

输出样例#1
1

输入样例#2
5 6
1 2 4
1 4 2
2 3 1
4 3 5
3 5 4
4 5 3

输出样例#2
11

首先咱们算一下样例

1 2 1

说明1到2的权值为1

然后结束

输出1；

第二组样例

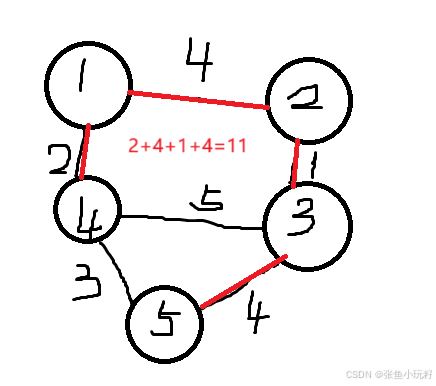
懂了吗

懂了就开始速通吧！

代码如下

#include<bits/stdc++.h>
using namespace std;
const int N=1510;
int n,m,u,v,w,ind[N],dp[N];
vector<int>g[N],g1[N];
queue<int>q;
int main(){
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		cin>>u>>v>>w;
		g[u].push_back(v);
		g1[u].push_back(w);
		ind[v]++;
	}
	for(int i=1;i<=n;i++){
		dp[i]=-1e9;
		if(ind[i]==0)q.push(i);
	}
	dp[1]=0;
	while(!q.empty()){
		int x=q.front();q.pop(); 
		for(int i=0;i<g[x].size();i++){
			int y=g[x][i];
			dp[y]=max(dp[y],g1[x][i]+dp[x]);
			if(--ind[y]==0)q.push(y);
		}
	} 
	if(dp[n]==-1e9)cout<<-1;
	else cout<<dp[n];
	return 0;
} 
//作者纯手搓，可以参考一下呦！

结语：速通成功，用时？秒。