C C++最全排序算法总结大全(C C++语言实现)_用c和c 输出常见排序算法(1)，C C++开发教程入门

本文链接：https://blog.youkuaiyun.com/2401_84978525/article/details/138878128

网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。

一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！

        for (j = i - increment; j >= 0 && tmp < arr[j]; j -= increment) {  
            arr[j + increment] = arr[j];  
        }  
        arr[j + increment] = tmp;
    }  
}

}

int main() {
int array[5] = {1,4,5,2,8};
ShellSort(array, 5);
for(int i = 0; i < 5; i++) {
printf(“%d\n”,array[i]);
}
}


##### 4.4 算法分析


希尔排序的核心在于间隔序列的设定。既可以提前设定好间隔序列，也可以动态的定义间隔序列。动态定义间隔序列的算法是《算法（第4版）》的合著者Robert Sedgewick提出的。


#### 5、归并排序（Merge Sort）


归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。


##### 5.1 算法描述


* 把长度为n的输入序列分成两个长度为n/2的子序列；
* 对这两个子序列分别采用归并排序；
* 将两个排序好的子序列合并成一个最终的排序序列。


##### 5.2 动图演示


![img](https://img-blog.csdnimg.cn/img_convert/2f9f62d486be19b87a3f37f13eb75786.png)


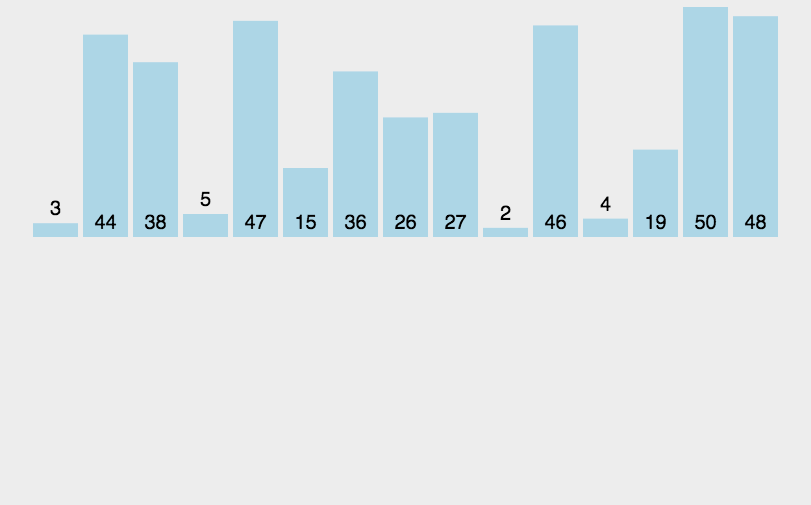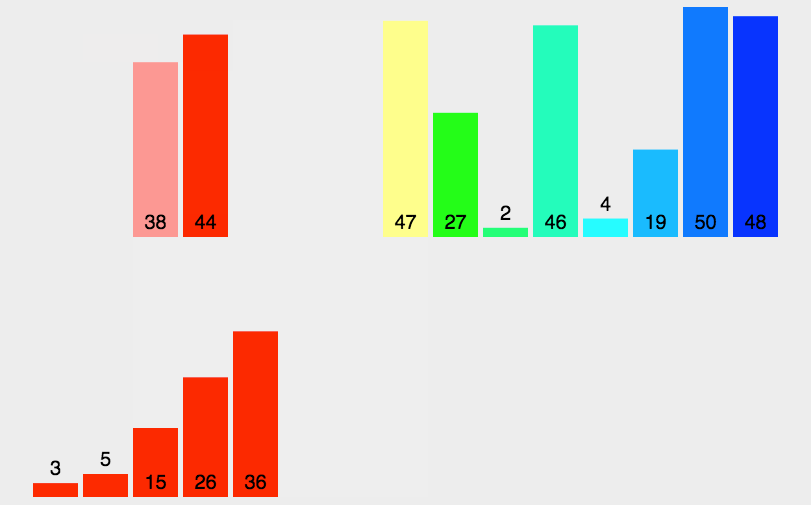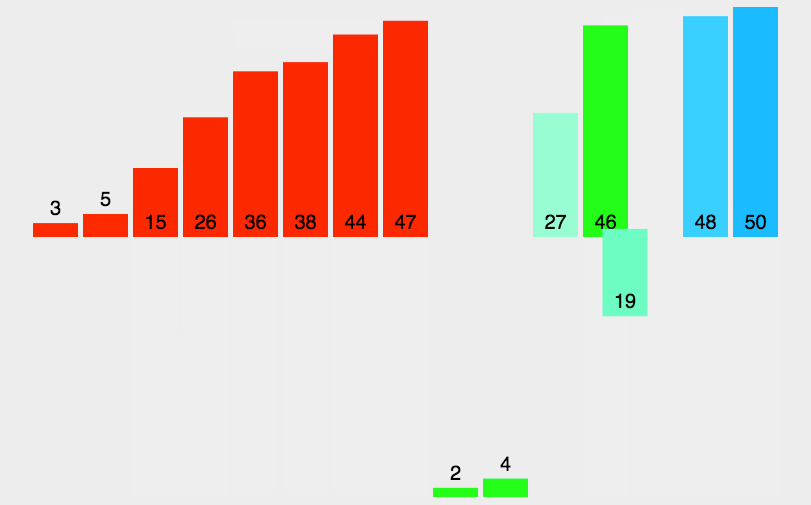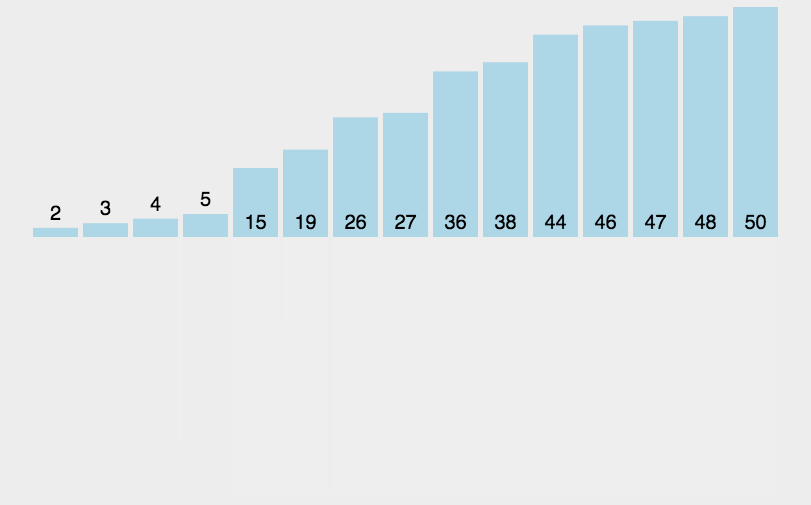
##### 5.3 代码实现

#define MAXSIZE 100

void Merge(int *SR, int *TR, int i, int middle, int rightend)
{
int j, k, l;
for (k = i, j = middle + 1; i <= middle && j <= rightend; k++) {
if (SR[i] < SR[j]) {
TR[k] = SR[i++];
} else {
TR[k] = SR[j++];
}
}
if (i <= middle) {
for (l = 0; l <= middle - i; l++) {
TR[k + l] = SR[i + l];
}
}
if (j <= rightend) {
for (l = 0; l <= rightend - j; l++) {
TR[k + l] = SR[j + l];
}
}
}

void MergeSort(int *SR, int *TR1, int s, int t)
{
int middle;
int TR2[MAXSIZE + 1];
if (s == t) {
TR1[s] = SR[s];
} else {
middle = (s + t) / 2;
MergeSort(SR, TR2, s, middle);
MergeSort(SR, TR2, middle + 1, t);
Merge(TR2, TR1, s, middle, t);
}
}


##### 5.4 算法分析


归并排序是一种稳定的排序方法。和选择排序一样，归并排序的性能不受输入数据的影响，但表现比选择排序好的多，因为始终都是O(nlogn）的时间复杂度。代价是需要额外的内存空间。


#### 6、快速排序（Quick Sort）


快速排序的基本思想：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。


##### 6.1 算法描述


快速排序使用分治法来把一个串（list）分为两个子串（sub-lists）。具体算法描述如下：


* 从数列中挑出一个元素，称为 “基准”（pivot）；
* 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
* 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。


##### 6.2 动图演示


![img](https://img-blog.csdnimg.cn/img_convert/eaca66d26efe27519e8c462d3a7d4593.png)


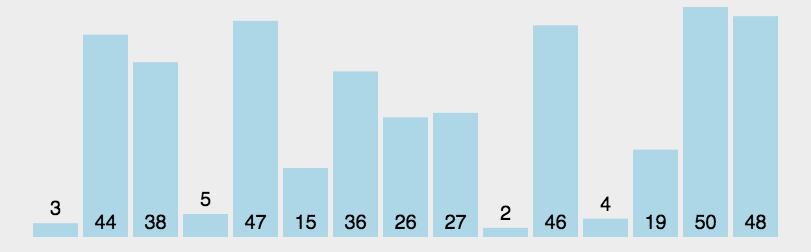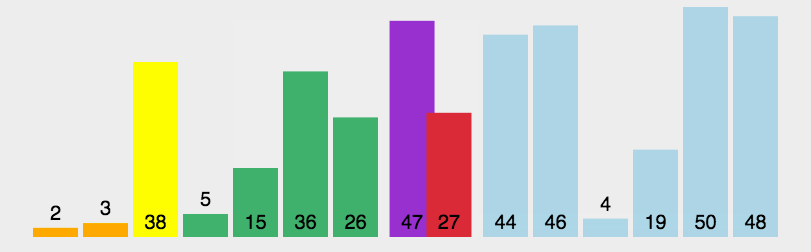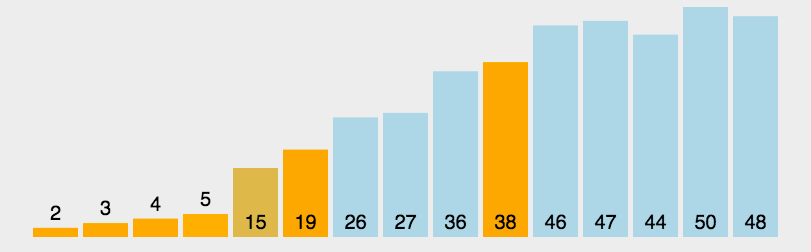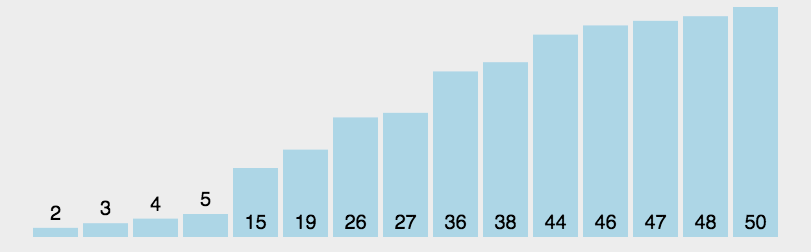
##### 6.3 代码实现

#include <stdio.h>

void swap(int *a, int *b)
{
int temp;
temp = *a;
*a = *b;
*b = temp;
}

void QuickSort(int *arr, int maxlen, int begin, int end)
{
int i, j;
if (begin < end) {
i = begin + 1;
j = end;
while (i < j) {
if(arr[i] > arr[begin]) {
swap(&arr[i], &arr[j]);
j–;
} else {
i++;
}
}
if (arr[i] >= arr[begin]) {
i–;
}
swap(&arr[begin], &arr[i]);
QuickSort(arr, maxlen, begin, i);
QuickSort(arr, maxlen, j, end);
}
}

int main() {
int array[5] = {1,4,5,2,8};
QuickSort(array, 5, 1, 4);
for(int i = 0; i < 5; i++) {
printf(“%d\n”,array[i]);
}
}


#### 7、堆排序（Heap Sort）


堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。


##### 7.1 算法描述


* 将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆，此堆为初始的无序区；
* 将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n]；
* 由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。


##### 7.2 动图演示


![img](https://img-blog.csdnimg.cn/img_convert/93824bbcbb3c16dbfd58a0e64d2c7c3c.png)


##### 7.3 代码实现

#include <stdio.h>
#include <stdlib.h>

void swap(int *a, int *b) {
int temp = *b;
*b = *a;
*a = temp;
}

void max_heapify(int arr[], int start, int end) {
// 建立父節點指標和子節點指標
int dad = start;
int son = dad * 2 + 1;
while (son <= end) { // 若子節點指標在範圍內才做比較
if (son + 1 <= end && arr[son] < arr[son + 1]) // 先比較兩個子節點大小，選擇最大的
son++;
if (arr[dad] > arr[son]) //如果父節點大於子節點代表調整完畢，直接跳出函數
return;
else { // 否則交換父子內容再繼續子節點和孫節點比較
swap(&arr[dad], &arr[son]);
dad = son;
son = dad * 2 + 1;
}
}
}

void heap_sort(int arr[], int len) {
int i;
// 初始化，i從最後一個父節點開始調整
for (i = len / 2 - 1; i >= 0; i–)
max_heapify(arr, i, len - 1);
// 先將第一個元素和已排好元素前一位做交換，再重新調整，直到排序完畢
for (i = len - 1; i > 0; i–) {
swap(&arr[0], &arr[i]);
max_heapify(arr, 0, i - 1);
}
}

int main() {
int arr[] = { 3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6 };
int len = (int) sizeof(arr) / sizeof(*arr);
heap_sort(arr, len);
int i;
for (i = 0; i < len; i++)
printf(“%d “, arr[i]);
printf(”\n”);
return 0;
}


#### 8、计数排序（Counting Sort）


计数排序不是基于比较的排序算法，其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。


##### 8.1 算法描述


* 找出待排序的数组中最大和最小的元素；
* 统计数组中每个值为i的元素出现的次数，存入数组C的第i项；
* 对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）；
* 反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。


##### 8.2 动图演示


![img](https://img-blog.csdnimg.cn/img_convert/25fdb31acd81f931cd443cb932140ab9.png)


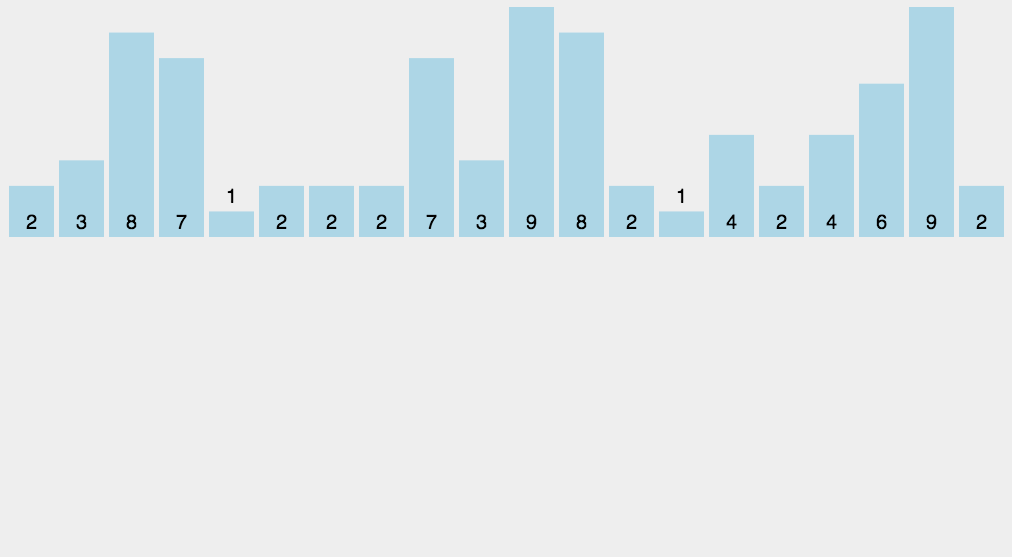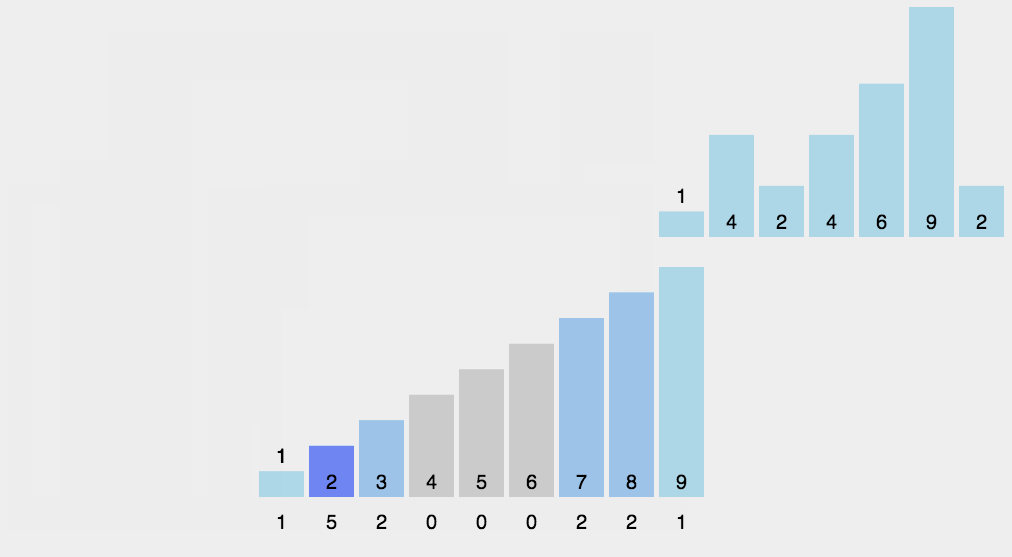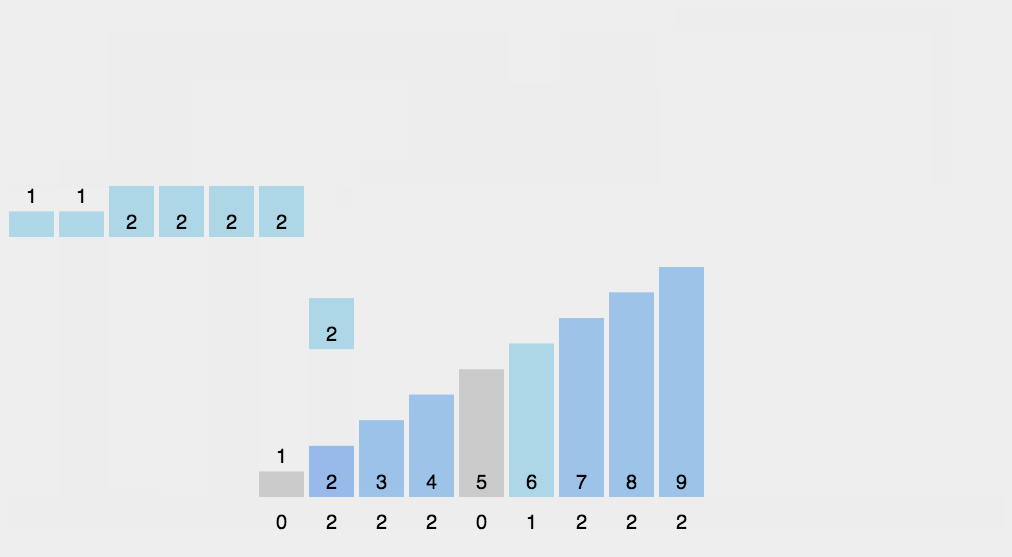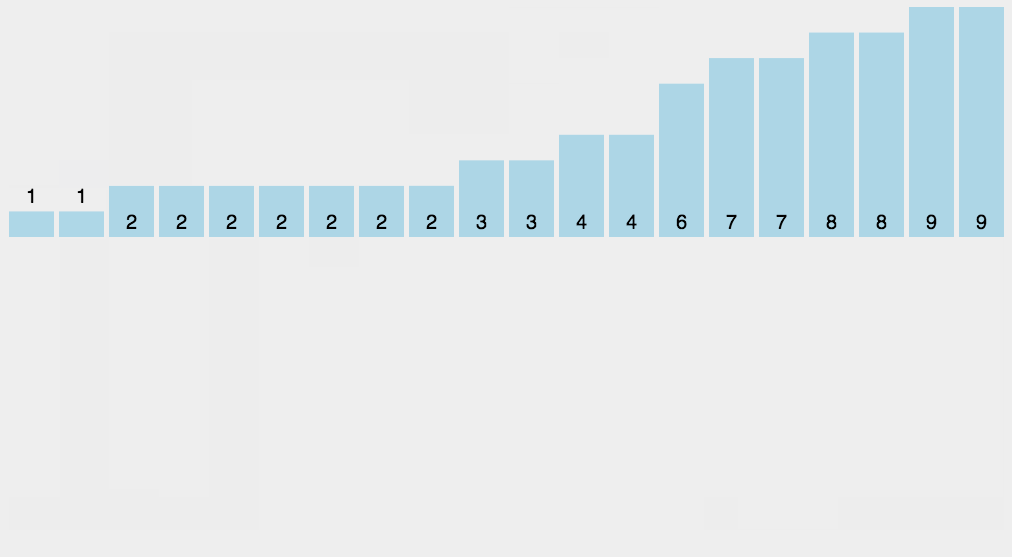
##### 8.3 代码实现

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

void print_arr(int *arr, int n) {
int i;
printf(“%d”, arr[0]);
for (i = 1; i < n; i++)
printf(" %d", arr[i]);
printf(“\n”);
}

void counting_sort(int *ini_arr, int *sorted_arr, int n) {
int *count_arr = (int *) malloc(sizeof(int) * 100);
int i, j, k;
for (k = 0; k < 100; k++)
count_arr[k] = 0;
for (i = 0; i < n; i++)
count_arr[ini_arr[i]]++;
for (k = 1; k < 100; k++)
count_arr[k] += count_arr[k - 1];
for (j = n; j > 0; j–)
sorted_arr[–count_arr[ini_arr[j - 1]]] = ini_arr[j - 1];
free(count_arr);
}

int main(int argc, char **argv) {
int n = 10;
int i;
int *arr = (int *) malloc(sizeof(int) * n);
int *sorted_arr = (int *) malloc(sizeof(int) * n);
srand(time(0));
for (i = 0; i < n; i++)
arr[i] = rand() % 100;
printf("ini_array: ");
print_arr(arr, n);
counting_sort(arr, sorted_arr, n);
printf("sorted_array: ");
print_arr(sorted_arr, n);
free(arr);
free(sorted_arr);
return 0;
}


##### 8.4 算法分析


计数排序是一个稳定的排序算法。当输入的元素是 n 个 0到 k 之间的整数时，时间复杂度是O(n+k)，空间复杂度也是O(n+k)，其排序速度快于任何比较排序算法。当k不是很大并且序列比较集中时，计数排序是一个很有效的排序算法。


#### 9、桶排序（Bucket Sort）


桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。桶排序 (Bucket sort)的工作的原理：假设输入数据服从均匀分布，将数据分到有限数量的桶里，每个桶再分别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排）。


##### 9.1 算法描述


* 设置一个定量的数组当作空桶；
* 遍历输入数据，并且把数据一个一个放到对应的桶里去；
* 对每个不是空的桶进行排序；
* 从不是空的桶里把排好序的数据拼接起来。


##### 9.2 图片演示


![img](https://img-blog.csdnimg.cn/img_convert/10985616f3ad0efb2433ed2c232a3bf6.png)


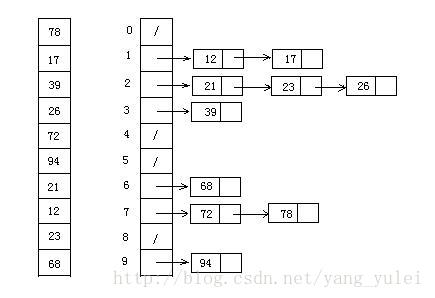
##### 9.3 代码实现

#include <stdio.h>
#include <string.h>

void bucketSort(int *arr, int size, int max)
{
int i,j;
int buckets[max];
memset(buckets, 0, max * sizeof(int));
for (i = 0; i < size; i++) {
buckets[arr[i]]++;
}
for (i = 0, j = 0; i < max; i++) {
while((buckets[i]–) >0)
arr[j++] = i;
}
}

int main() {
int array[5] = {1,4,5,2,8};
bucketSort(array, 5, 100);
for(int i = 0; i < 5; i++) {
printf(“%d\n”,array[i]);
}
}


##### 9.4 算法分析


桶排序最好情况下使用线性时间O(n)，桶排序的时间复杂度，取决与对各个桶之间数据进行排序的时间复杂度，因为其它部分的时间复杂度都为O(n)。很显然，桶划分的越小，各个桶之间的数据越少，排序所用的时间也会越少。但相应的空间消耗就会增大。


#### 10、基数排序（Radix Sort）


基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。


##### 10.1 算法描述


* 取得数组中的最大数，并取得位数；
* arr为原始数组，从最低位开始取每个位组成radix数组；
* 对radix进行计数排序（利用计数排序适用于小范围数的特点）；


##### 10.2 动图演示


![img](https://img-blog.csdnimg.cn/img_convert/88cb17eb223c8838182dcaff3dfcde17.png)


##### 10.3 代码实现

#include <stdio.h>
#include <string.h>

int get_index(int num, int dec, int order)
{
int i, j, n;
int index;
int div;
for (i = dec; i > order; i–) {
n = 1;
for (j = 0; j < dec - 1; j++)
n *= 10;
div = num / n;
num -= div * n;
dec–;
}
n = 1;
for (i = 0; i < order - 1; i++)
n *= 10;
index = num / n;
return index;
}

void RadixSort(int *arr, int len, int dec, int order)
{
int i, j;
int index;
int tmp[len];
int num[10];
memset(num, 0, 10 * sizeof(int));
memset(tmp, 0, len * sizeof(int));

if (dec < order) {
    return;
}
for (i = 0; i < len; i++) {
    index = get\_index(arr[i], dec, order);
    num[index]++; 
}

for (i = 1; i < 10; i++) {
    num[i] += num[i-1];
}
for (i = len - 1; i >= 0; i--) {
    index = get\_index(arr[i], dec, order); 
    j = --num[index]; 
    tmp[j] = arr[i]; 
}

for (i = 0; i < len; i++) {
    arr[i] = tmp[i]; 
}
RadixSort(arr, len, dec, order+1);

}

int main() {
int array[5] = {1,4,5,2,8};
RadixSort(array, 5, 0, 0);
for(int i = 0; i < 5; i++) {
printf(“%d\n”,array[i]);
}
}


##### 10.4 算法分析


基数排序基于分别排序，分别收集，所以是稳定的。但基数排序的性能比桶排序要略差，每一次关键字的桶分配都需要O(n)的时间复杂度，而且分配之后得到新的关键字序列又需要O(n)的时间复杂度。假如待排数据可以分为d个关键字，则基数排序的时间复杂度将是O(d\*2n) ，当然d要远远小于n，因此基本上还是线性级别的。



![img](https://img-blog.csdnimg.cn/img_convert/03f2ccbb466c752e794c2bd4f71788bc.png)
![img](https://img-blog.csdnimg.cn/img_convert/e921bd3d9362dd29499a71c6342343c2.png)

**网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。**

**[需要这份系统化的资料的朋友，可以添加戳这里获取](https://bbs.youkuaiyun.com/topics/618668825)**


**一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！**

法分析


基数排序基于分别排序，分别收集，所以是稳定的。但基数排序的性能比桶排序要略差，每一次关键字的桶分配都需要O(n)的时间复杂度，而且分配之后得到新的关键字序列又需要O(n)的时间复杂度。假如待排数据可以分为d个关键字，则基数排序的时间复杂度将是O(d\*2n) ，当然d要远远小于n，因此基本上还是线性级别的。



[外链图片转存中...(img-zpzew2Tq-1715707220622)]
[外链图片转存中...(img-SgjWk1id-1715707220622)]

**网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。**

**[需要这份系统化的资料的朋友，可以添加戳这里获取](https://bbs.youkuaiyun.com/topics/618668825)**


**一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！**