C C++最全【C++】如何用一棵红黑树同时封装出set与map，C C++模块化面向接口编程-优快云博客

本文链接：https://blog.youkuaiyun.com/2401_84975986/article/details/138874613

网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。

一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！

public:
//…
private:
Node* _root;
}


即：


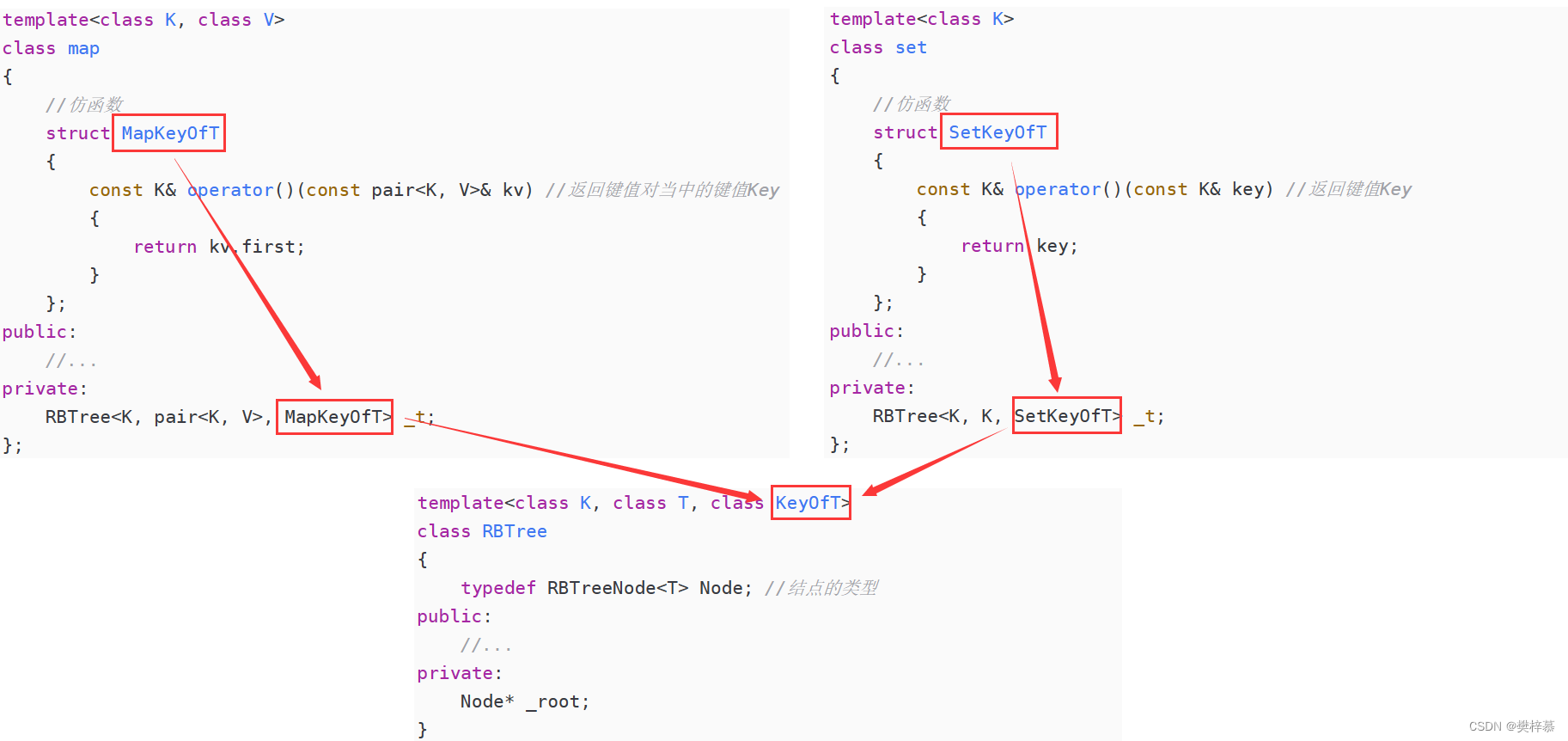
![](https://img-blog.csdnimg.cn/direct/3eaa4c313b464a099a5587127906a468.png)


在实现红黑树时，只需要创建这个KeyOfT类对象，就相当于实例化了对应的set或map中实际的方法，比如：

//查找函数
iterator Find(const K& key)
{
KeyOfT kot;
Node* cur = _root;
while (cur)
{
if (key < kot(cur->_data)) //key值小于该结点的值
{
cur = cur->_left; //在该结点的左子树当中查找
}
else if (key > kot(cur->_data)) //key值大于该结点的值
{
cur = cur->_right; //在该结点的右子树当中查找
}
else //找到了目标结点
{
return iterator(cur); //返回该结点
}
}
return end(); //查找失败
}


所以对于红黑树来说，所有对应的需要比较的部分我们都需要进行修改。 




---


## 4.红黑树的正向迭代器


红黑树的正向迭代器实际上就是对结点指针进行了封装，因此在正向迭代器当中实际上就只有一个成员变量，那就是正向迭代器所封装结点的指针。


### 4.1迭代器的定义

//正向迭代器
template<class T, class Ref, class Ptr>
struct __TreeIterator
{
typedef RBTreeNode Node; //结点的类型
typedef __TreeIterator<T, Ref, Ptr> Self; //正向迭代器的类型

Node* _node; //正向迭代器所封装结点的指针
};


### 4.2迭代器的构造


我们通过一个结点的指针便可以构造出一个正向迭代器。

//构造函数
__TreeIterator(Node* node)
:_node(node) //根据所给结点指针构造一个正向迭代器
{}


### 4.3重载解引用操作符 \*


当对正向迭代器进行解引用操作时，我们直接返回对应结点数据的引用即可。

Ref operator*()
{
return _node->_data; //返回结点数据的引用
}


### 4.4重载箭头操作符 ->


当对正向迭代器进行->操作时，我们直接返回对应结点数据的指针即可。

Ptr operator->()
{
return &_node->_data; //返回结点数据的指针
}



> 
> 注意：这里与链表List部分的->操作符重载一样，返回的是地址，即使用时为了可读性省略了一个->。 
> 
> 
> 


### 4.5重载 == 和 != 操作符


实现时直接判断两个迭代器所封装的结点是否是同一个即可。

//判断两个正向迭代器是否不同
bool operator!=(const Self& s) const
{
return _node != s._node; //判断两个正向迭代器所封装的结点是否是同一个
}
//判断两个正向迭代器是否相同
bool operator==(const Self& s) const
{
return _node == s._node; //判断两个正向迭代器所封装的结点是否是同一个
}




---


### 4.6重载 ++、-- 操作符


之前链表List迭代器的 ++ 操作符重载的逻辑非常简单，只需要 node=node->next即可，但是对于一棵二叉搜索树而言显然不会这么简单。


那么按照搜索的逻辑，我们知道++应该得到的是中序遍历的后一个节点。


![](https://img-blog.csdnimg.cn/direct/b7e17353a3544992b5fbb9f752d850db.png)


根据图像我们可以推导出 ++ 的逻辑： 


1. 如果当前结点的右子树不为空，则`++`操作后应该找到其右子树当中的最左结点。
2. 如果当前结点的右子树为空，则`++`操作后应该在该结点的祖先结点中，找到孩子不在父亲右的祖先。




---

//前置++
Self operator++()
{
if (_node->_right) //结点的右子树不为空
{
//寻找该结点右子树当中的最左结点
Node* left = _node->_right;
while (left->_left)
{
left = left->_left;
}
_node = left; //++后变为该结点
}
else //结点的右子树为空
{
//寻找孩子不在父亲右的祖先
Node* cur = _node;
Node* parent = cur->_parent;
while (parent&&cur == parent->_right)
{
cur = parent;
parent = parent->_parent;
}
_node = parent; //++后变为该结点
}
return *this;
}


那么同样的对于 -- 操作符的逻辑如下：


1. 如果当前结点的左子树不为空，则`--`操作后应该找到其左子树当中的最右结点。
2. 如果当前结点的左子树为空，则`--`操作后应该在该结点的祖先结点中，找到孩子不在父亲左的祖先。




---

//前置–
Self operator–()
{
if (_node->_left) //结点的左子树不为空
{
//寻找该结点左子树当中的最右结点
Node* right = _node->_left;
while (right->_right)
{
right = right->_right;
}
_node = right; //–后变为该结点
}
else //结点的左子树为空
{
//寻找孩子不在父亲左的祖先
Node* cur = _node;
Node* parent = cur->_parent;
while (parent&&cur == parent->_left)
{
cur = parent;
parent = parent->_parent;
}
_node = parent; //–后变为该结点
}
return *this;
}


正向迭代器实现后，我们需要在红黑树的实现当中进行迭代器类型的typedef。



> 
> 需要注意的是，为了让外部能够使用typedef后的正向迭代器类型iterator，我们需要在public区域进行typedef。
> 
> 
> 


然后在红黑树当中实现成员函数begin和end：


* begin函数返回中序序列当中第一个结点的正向迭代器，即最左结点。
* end函数返回中序序列当中最后一个结点下一个位置的正向迭代器，这里直接用空指针构造一个正向迭代器。

template<class K, class T, class KeyOfT>
class RBTree
{
typedef RBTreeNode Node; //结点的类型
public:
typedef __TreeIterator<T, T&, T*> iterator; //正向迭代器

iterator begin()
{
	//寻找最左结点
	Node* left = _root;
	while (left&&left->_left)
	{
		left = left->_left;
	}
	//返回最左结点的正向迭代器
	return iterator(left);
}
iterator end()
{
	//返回由nullptr构造得到的正向迭代器（不严谨）
	return iterator(nullptr);
}

private:
Node* _root; //红黑树的根结点
};


但这样实现的end()迭代器其实并不符合要求，因为如果对end()位置的迭代器--后，应该得到最后一个位置的正向迭代器，但这里很明显无法实现。


实际上在STL库中是这样设计的：


在红黑树的根节点新增一个头节点，这个头结点的左孩子为最左节点，右孩子为最右节点。


在这样的结构下，正向迭代器的begin()只需用头节点的左孩子构造即可，反向迭代器的rbegin()只需用头结点的右孩子构造出一个正向迭代器然后再对该正向迭代器进行封装，得到反向迭代器即可。end和rend()


但是如果红黑树加入了这个头节点，就会改变之前我们实现的红黑树的很多逻辑，这里就不实现了。




---


## 5.红黑树的反向迭代器


还记得我们之前学习过的反向迭代器的实现么？


[【C++】反向迭代器模拟实现-优快云博客![icon-default.png?t=N7T8](https://csdnimg.cn/release/blog_editor_html/release2.3.6/ckeditor/plugins/CsdnLink/icons/icon-default.png?t=N7T8)https://blog.youkuaiyun.com/2301\_77112634/article/details/135837568?spm=1001.2014.3001.5502](https://blog.youkuaiyun.com/2301_77112634/article/details/135837568?spm=1001.2014.3001.5502 "【C++】反向迭代器模拟实现-优快云博客")


反向迭代器需不需要我们从零开始写呢？还是和适配器一样，利用普通迭代器的结构满足反向迭代器的特性即可？这样是不是比较方便？


* rbegin()相当于end()
* rend()相当于begin()
* 反向迭代器++相当于正向迭代器--
* 其他操作\* != ->和正向迭代器相同

//反向迭代器—迭代器适配器
template
struct ReverseIterator
{
typedef ReverseIterator Self; //反向迭代器的类型

//限定符不能区分静态变量和类型，所以前面可以加上typename标识为类型
typedef typename Iterator::reference Ref; //结点指针的引用
typedef typename Iterator::pointer Ptr; //结点指针

Iterator _it; //反向迭代器所封装的正向迭代器

//构造函数
ReverseIterator(Iterator it)
	:_it(it) //根据所给正向迭代器构造一个反向迭代器
{}

Ref operator*()
{
	return *_it; //通过调用正向迭代器的operator*返回结点数据的引用
}
Ptr operator->()
{
	return _it.operator->(); //通过调用正向迭代器的operator->返回结点数据的指针
}

//前置++
Self& operator++()
{
	--_it; //调用正向迭代器的前置--
	return *this;
}
//前置--
Self& operator--()
{
	++_it; //调用正向迭代器的前置++
	return *this;
}

bool operator!=(const Self& s) const
{
	return _it != s._it; //调用正向迭代器的operator!=
}
bool operator==(const Self& s) const
{
	return _it == s._it; //调用正向迭代器的operator==
}

};


需要注意的是，反向迭代器只接收了一个模板参数，即正向迭代器的类型，也就是说，反向迭代器不知道结点的引用类型和结点的指针类型，因此我们需要在正向迭代器当中对这两个类型进行typedef，这样反向迭代器才能通过正向迭代器获取结点的引用类型和结点的指针类型。

//正向迭代器
template<class T, class Ref, class Ptr>
struct __TreeIterator
{
typedef Ref reference; //结点指针的引用
typedef Ptr pointer; //结点指针
};


反向迭代器的rbegin()：红黑树的最右节点；


反向迭代器的rend()：空指针构造；

template<class K, class T, class KeyOfT>
class RBTree
{
typedef RBTreeNode Node; //结点的类型
public:
typedef ReverseIterator reverse_iterator; //反向迭代器

reverse_iterator rbegin()
{
	//寻找最右结点
	Node* right = _root;
	while (right&&right->_right)
	{
		right = right->_right;
	}
	//返回最右结点的反向迭代器
	return reverse_iterator(iterator(right));
}
reverse_iterator rend()
{
	//返回由nullptr构造得到的反向迭代器（不严谨）
	return reverse_iterator(iterator(nullptr));
}

private:
Node* _root; //红黑树的根结点
};




---


注意：此时迭代器指向的值可以被修改，而在set中我们存储的是<K,K>,map中存储的是<K,pair<K,V>>，为了防止二叉树遭到破坏，所以我们需要进行类似这样的处理：


* set<K,const K>;
* map<K,pair<const K,V>>;




---


## 6.完整代码


### RBTree.h

#pragma once

//枚举定义结点的颜色
enum Colour
{
RED,
BLACK
};

//红黑树结点的定义
template
struct RBTreeNode
{
//三叉链
RBTreeNode* _left;
RBTreeNode* _right;
RBTreeNode* _parent;

//存储的数据
T _data;

//结点的颜色
int _col; //红/黑

//构造函数
RBTreeNode(const T& data)
	: _left(nullptr)
	, _right(nullptr)
	, _parent(nullptr)
	, _data(data)
	, _col(RED)
{}

};

//正向迭代器
template<class T, class Ref, class Ptr>
struct __TreeIterator
{
typedef Ref reference; //结点指针的引用
typedef Ptr pointer; //结点指针

typedef RBTreeNode<T> Node; //结点的类型
typedef __TreeIterator<T, Ref, Ptr> Self; //正向迭代器的类型

Node* _node; //正向迭代器所封装结点的指针

//构造函数
__TreeIterator(Node* node)
	:_node(node) //根据所给结点指针构造一个正向迭代器
{}

Ref operator*()
{
	return _node->_data; //返回结点数据的引用
}
Ptr operator->()
{
	return &_node->_data; //返回结点数据的指针
}
//判断两个正向迭代器是否不同
bool operator!=(const Self& s) const
{
	return _node != s._node; //判断两个正向迭代器所封装的结点是否是同一个
}
//判断两个正向迭代器是否相同
bool operator==(const Self& s) const
{
	return _node == s._node; //判断两个正向迭代器所封装的结点是否是同一个
}

//前置++
Self operator++()
{
	if (_node->_right) //结点的右子树不为空
	{
		//寻找该结点右子树当中的最左结点
		Node* left = _node->_right;
		while (left->_left)
		{
			left = left->_left;
		}
		_node = left; //++后变为该结点
	}
	else //结点的右子树为空
	{
		//寻找孩子不在父亲右的祖先
		Node* cur = _node;
		Node* parent = cur->_parent;
		while (parent && cur == parent->_right)
		{
			cur = parent;
			parent = parent->_parent;
		}
		_node = parent; //++后变为该结点
	}
	return *this;
}

//前置--
Self operator--()
{
	if (_node->_left) //结点的左子树不为空
	{
		//寻找该结点左子树当中的最右结点
		Node* right = _node->_left;
		while (right->_right)
		{
			right = right->_right;
		}
		_node = right; //--后变为该结点
	}
	else //结点的左子树为空
	{
		//寻找孩子不在父亲左的祖先
		Node* cur = _node;
		Node* parent = cur->_parent;
		while (parent && cur == parent->_left)
		{
			cur = parent;
			parent = parent->_parent;
		}
		_node = parent; //--后变为该结点
	}
	return *this;
}

};

//反向迭代器—迭代器适配器
template
struct ReverseIterator
{
typedef ReverseIterator Self; //反向迭代器的类型
typedef typename Iterator::reference Ref; //结点指针的引用
typedef typename Iterator::pointer Ptr; //结点指针

Iterator _it; //反向迭代器所封装的正向迭代器

//构造函数
ReverseIterator(Iterator it)
	:_it(it) //根据所给正向迭代器构造一个反向迭代器
{}

Ref operator*()
{
	return *_it; //通过调用正向迭代器的operator*返回结点数据的引用
}
Ptr operator->()
{
	return _it.operator->(); //通过调用正向迭代器的operator->返回结点数据的指针
}

//前置++
Self& operator++()
{
	--_it; //调用正向迭代器的前置--
	return *this;
}
//前置--
Self& operator--()
{
	++_it; //调用正向迭代器的前置++
	return *this;
}

bool operator!=(const Self& s) const
{
	return _it != s._it; //调用正向迭代器的operator!=
}
bool operator==(const Self& s) const
{
	return _it == s._it; //调用正向迭代器的operator==
}

};

//红黑树的实现
template<class K, class T, class KeyOfT>
class RBTree
{
typedef RBTreeNode Node; //结点的类型
public:
typedef __TreeIterator<T, T&, T*> iterator; //正向迭代器
typedef ReverseIterator reverse_iterator; //反向迭代器

reverse_iterator rbegin()
{
	//寻找最右结点
	Node* right = _root;
	while (right && right->_right)
	{
		right = right->_right;
	}
	//返回最右结点的反向迭代器
	return reverse_iterator(iterator(right));
}
reverse_iterator rend()
{
	//返回由nullptr构造得到的反向迭代器（不严谨）
	return reverse_iterator(iterator(nullptr));
}

iterator begin()
{
	//寻找最左结点
	Node* left = _root;
	while (left && left->_left)
	{
		left = left->_left;
	}
	//返回最左结点的正向迭代器
	return iterator(left);
}
iterator end()
{
	//返回由nullptr构造得到的正向迭代器（不严谨）
	return iterator(nullptr);
}
//构造函数
RBTree()
	:_root(nullptr)
{}

//拷贝构造
RBTree(const RBTree<K, T, KeyOfT>& t)
{
	_root = _Copy(t._root, nullptr);
}

//赋值运算符重载（现代写法）
RBTree<K, T, KeyOfT>& operator=(RBTree<K, T, KeyOfT> t)
{
	swap(_root, t._root);
	return *this; //支持连续赋值
}

//析构函数
~RBTree()
{
	_Destroy(_root);
	_root = nullptr;
}

//查找函数
iterator Find(const K& key)
{
	KeyOfT kot;
	Node* cur = _root;
	while (cur)
	{
		if (key < kot(cur->_data)) //key值小于该结点的值
		{
			cur = cur->_left; //在该结点的左子树当中查找
		}
		else if (key > kot(cur->_data)) //key值大于该结点的值
		{
			cur = cur->_right; //在该结点的右子树当中查找
		}
		else //找到了目标结点
		{
			return iterator(cur); //返回该结点
		}
	}
	return end(); //查找失败
}

//插入函数
pair<iterator, bool> Insert(const T& data)
{
	if (_root == nullptr) //若红黑树为空树，则插入结点直接作为根结点
	{
		_root = new Node(data);
		_root->_col = BLACK; //根结点必须是黑色
		return make_pair(iterator(_root), true); //插入成功
	}
	//1、按二叉搜索树的插入方法，找到待插入位置
	KeyOfT kot;
	Node* cur = _root;
	Node* parent = nullptr;
	while (cur)
	{
		if (kot(data) < kot(cur->_data)) //待插入结点的key值小于当前结点的key值
		{
			//往该结点的左子树走
			parent = cur;
			cur = cur->_left;
		}
		else if (kot(data) > kot(cur->_data)) //待插入结点的key值大于当前结点的key值
		{
			//往该结点的右子树走
			parent = cur;
			cur = cur->_right;
		}
		else //待插入结点的key值等于当前结点的key值
		{
			return make_pair(iterator(cur), false); //插入失败
		}
	}

	//2、将待插入结点插入到树中
	cur = new Node(data); //根据所给值构造一个结点
	Node* newnode = cur; //记录新插入的结点（便于后序返回）
	if (kot(data) < kot(parent->_data)) //新结点的key值小于parent的key值
	{
		//插入到parent的左边
		parent->_left = cur;
		cur->_parent = parent;
	}
	else //新结点的key值大于parent的key值
	{
		//插入到parent的右边
		parent->_right = cur;
		cur->_parent = parent;
	}

	//3、若插入结点的父结点是红色的，则需要对红黑树进行调整
	while (parent && parent->_col == RED)
	{
		Node* grandfather = parent->_parent; //parent是红色，则其父结点一定存在
		if (parent == grandfather->_left) //parent是grandfather的左孩子
		{
			Node* uncle = grandfather->_right; //uncle是grandfather的右孩子
			if (uncle && uncle->_col == RED) //情况1：uncle存在且为红
			{
				//颜色调整
				parent->_col = uncle->_col = BLACK;
				grandfather->_col = RED;

				//继续往上处理
				cur = grandfather;
				parent = cur->_parent;
			}
			else //情况2+情况3：uncle不存在 + uncle存在且为黑
			{
				if (cur == parent->_left)
				{
					RotateR(grandfather); //右单旋

					//颜色调整
					grandfather->_col = RED;
					parent->_col = BLACK;
				}
				else //cur == parent->_right
				{
					RotateLR(grandfather); //左右双旋

					//颜色调整
					grandfather->_col = RED;
					cur->_col = BLACK;
				}
				break; //子树旋转后，该子树的根变成了黑色，无需继续往上进行处理
			}
		}
		else //parent是grandfather的右孩子
		{
			Node* uncle = grandfather->_left; //uncle是grandfather的左孩子
			if (uncle && uncle->_col == RED) //情况1：uncle存在且为红
			{
				//颜色调整
				uncle->_col = parent->_col = BLACK;
				grandfather->_col = RED;

				//继续往上处理
				cur = grandfather;
				parent = cur->_parent;
			}
			else //情况2+情况3：uncle不存在 + uncle存在且为黑
			{
				if (cur == parent->_left)
				{
					RotateRL(grandfather); //右左双旋

					//颜色调整
					cur->_col = BLACK;
					grandfather->_col = RED;
				}
				else //cur == parent->_right
				{
					RotateL(grandfather); //左单旋

					//颜色调整
					grandfather->_col = RED;
					parent->_col = BLACK;
				}
				break; //子树旋转后，该子树的根变成了黑色，无需继续往上进行处理
			}
		}
	}
	_root->_col = BLACK; //根结点的颜色为黑色（可能被情况一变成了红色，需要变回黑色）
	return make_pair(iterator(newnode), true); //插入成功
}

private:
//拷贝树
Node* _Copy(Node* root, Node* parent)
{
if (root == nullptr)
{
return nullptr;
}
Node* copyNode = new Node(root->_data);
copyNode->_parent = parent;
copyNode->_left = _Copy(root->_left, copyNode);
copyNode->_right = _Copy(root->_right, copyNode);
return copyNode;
}

//析构函数子函数
void _Destroy(Node* root)
{
	if (root == nullptr)
	{
		return;
	}
	_Destroy(root->_left);
	_Destroy(root->_right);
	delete root;
}

既有适合小白学习的零基础资料，也有适合3年以上经验的小伙伴深入学习提升的进阶课程，涵盖了95%以上C C++开发知识点，真正体系化！

由于文件比较多，这里只是将部分目录截图出来，全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频，并且后续会持续更新

如果你需要这些资料，可以戳这里获取

oot->_col = BLACK; //根结点的颜色为黑色（可能被情况一变成了红色，需要变回黑色）
return make_pair(iterator(newnode), true); //插入成功
}

//析构函数子函数
void _Destroy(Node* root)
{
	if (root == nullptr)
	{
		return;
	}
	_Destroy(root->_left);
	_Destroy(root->_right);
	delete root;
}

[外链图片转存中…(img-TfJjvDRc-1715699900815)]
[外链图片转存中…(img-dgANdI6W-1715699900816)]

既有适合小白学习的零基础资料，也有适合3年以上经验的小伙伴深入学习提升的进阶课程，涵盖了95%以上C C++开发知识点，真正体系化！

由于文件比较多，这里只是将部分目录截图出来，全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频，并且后续会持续更新

如果你需要这些资料，可以戳这里获取