环形链表问题（判环+寻找入环点）_判断链表是否有环c++ 快慢指针(1)

最新推荐文章于 2025-03-23 20:31:33 发布

2401_84975963

最新推荐文章于 2025-03-23 20:31:33 发布

阅读量702

点赞数 15

文章标签： c语言 c++ 学习

本文链接：https://blog.youkuaiyun.com/2401_84975963/article/details/138983762

版权

网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。

需要这份系统化的资料的朋友，可以添加戳这里获取

一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！

bool hasCycle(struct ListNode \*head) {
    struct ListNode\* slow,\*fast;
    fast=slow=head;
    while(fast&&fast->next)
    {
        fast=fast->next->next;
        slow=slow->next;
        if(slow==fast)
            return true;
    }
    return false;
}

代码呢确实很简单，但是，还有一些问题值得我们来思考一下

1.2 思考：为什么快指针每次走两步，慢指针每次走一步两者一定可以相遇？

大家有没有想过为什么快指针每次走两步，慢指针每次走一步在带环的情况下两者一定可以相遇呢？

我们来一起证明一下：

慢指针slow一次走一步，我们假设慢指针进环的时候，fast和slow的距离是N

那此时fast和slow两个人都在环里，两者距离为N，而fast又比slow走得快，所以fast是不是就有可能追上slow。

那为什么fast一次走两步，slow一次走一步就一定可以追上呢？两者就一定会相遇呢？有没有可能会错过呢？

🆗，这样是一定可以相遇的：
此时两者都在环里，距离为N，fast一次走两步，slow一次走一步，所以它们的速度差是1。
也就是说，往后每走一次，两者的距离就缩小1
N，N-1，N-2，... ，3，2，1，0
那么N次之后，两者的距离就会缩小到0，此时两者就相遇了。

而且肯定在一圈之内就追上了，因为慢指针入环的时候，两者的距离肯定是小于环的周长的。

1.3 快指针一次走3步，走4步，…n步行吗？

那我们再来思考，上面我们证明了慢指针一次走一步，快指针一次走两步一定可以相遇。那么，快指针一次多走几步还可以吗？走3步，走4步，…n步行吗？

那这样的话能不能相遇就要看情况了，我们来分析一下，比如，我们以快指针每次走3步来分析一下（其它情况也类似）：

慢指针slow呢还是一次走一步，那我们还是假设当slow走到入环点的时候，两者距离为N
slow进入环之后呢，fast就开始追击slow了。
那么此时fast一次走3步，slow一次走1步，即它们的速度差是2，也就是说，每追击一次，两者的距离缩小2
那此时它们还一定会相遇吗？
🆗，此时就要分情况看了：
如果N是偶数，那么N每次-2，最终一定可以减小到0，那就可以相遇。
如果N是奇数，每次-2，最终会减到...3，1，-1
那当它们的距离N变成-1的时候，意味着什么？
两者是不是错过了啊。fast直接跳到了slow前面距离为1的位置。
那此时两者的距离又变成了多少？

如果假设环的周长是C，那他们的距离就变成了C-1，然后fast重新开始追击slow，那这次能相遇吗？
是不是又取决于它们的新距离C-1是奇数还是偶数啊？
每次追击距离缩小2，如果C-1是偶数可以相遇，如果C-1是奇数那么将永远追不上了！
因为C-1是奇数的话，最终又会减到-1，减到-1的话它们的距离就还是C-1，C-1是奇数，最终又会减到-1，减到-1的话它们的距离就还是C-1…
就会一直循环下去，永远追不上！！！

而C-1到底是奇数还是偶数，我们不知道，这取决与环的大小。

那如果每次fast走的更多，走4步，5步，…n步也是一样的：

就看它们在对应的速度差下距离能不能缩小到0，slow入环时距离为N，假设速度差是gap，N每次减去gap，如果最终可以减到0，就可以相遇（即看N是不是gap的整数倍）。
如果最终不能减到0，那他们就会错过，假设错过之后距离为C-X，如果C-X是速度差gap的整数倍，那还可以相遇，如果不是，那就永远不能相遇。

所以：

如果快慢指针的速度差是1，那么一定可以追上相遇，如果大于1，就不一定了。

题目2. 寻找入环点

那么下面我们再来看一道环形链表的题目
链接: link
在这里插入图片描述
这道题呢，我们不仅要判断链表有没有环，还要返回入环的结点，如果链表无环，则返回 null。

2.1 思路1

这道题单要写代码的话呢其实很简单，有一个方法是这样的：

上面我们刚做了一道题不是判断链表是否带环嘛，用快慢指针如果最终可以相遇的话就是有环。
那现在要寻找入环点，就可以这样：
让一个指针从链表起始位置开始遍历链表，同时让一个指针从判环时相遇点的位置开始绕环运行，两个指针都是每次均走一步，最终就一定会在入环点相遇。

2.2 代码实现

那我们来写一下代码，看看能不能通过：

🆗，就过啦！

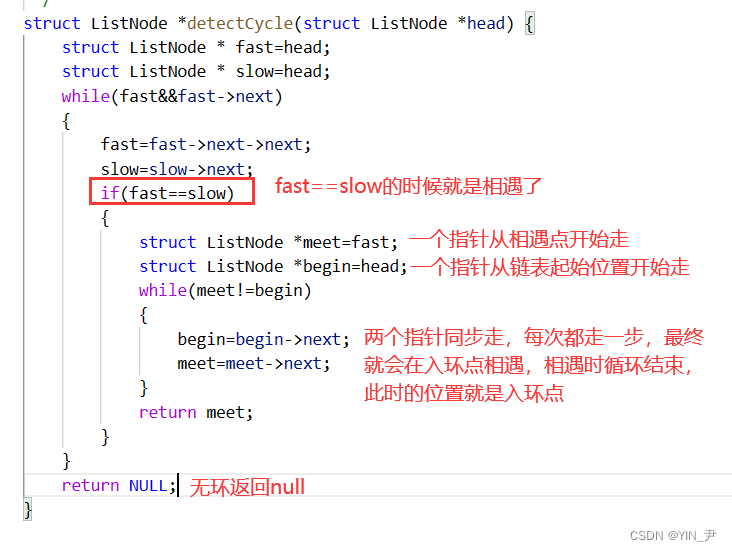
struct ListNode \*detectCycle(struct ListNode \*head) {
    struct ListNode \* fast=head;
    struct ListNode \* slow=head;
    while(fast&&fast->next)
    {
        fast=fast->next->next;
        slow=slow->next;
        if(fast==slow)
        {
            struct ListNode \*meet=fast;
            struct ListNode \*begin=head;
            while(meet!=begin)
            {
                begin=begin->next;
                meet=meet->next;
            }
            return meet;
        }
    }
    return NULL;
}

但是，为什么一个指针从判环的相遇点开始走，一个指针从链表起始位置走，就一定会在入环点相遇呢？

那下面我们来证明一下这个结论

2.3 证明：为什么一个指针从相遇点开始走，一个指针从链表起始位置走，两者会在入环点相遇？

那我们依然还是来画图分析一下：

我们假设链表起点到入环点的距离为L，入环点到相遇点的距离为N，那相遇点在往前走到入环点的距离就是C-N。
那么快慢指针在相遇的时候，所走的路程：
慢指针slow：L+N
ps：慢指针在环内走的距离不会超过一圈的，上一题我们分析了，慢指针入环时两者的距离肯定小于N，一圈之内就追上了。
快指针fast：L+k*C+N
解释：快慢指针相遇时，快指针fast已经绕环走了k圈了，k至少为1。因为fast先进入环，而且速度快，所以一定先独自经过相遇点M，而最终两者又在M相遇。所以fast至少绕环走了一整圈再+N走到相遇点。
即k至少为1，至于具体的大小还取决于环的大小，环长C相对于L越小，k就越大。

然后：

又因为快指针的速度是慢指针的2倍，所以：
相遇时快指针的路程是慢指针的2倍，即
L+k*C+N=2*(L+N)
k*C=L+N
所以：
L=k*C-N，即：
L=(k-1)*C+C-N

那我们再来看图：
L=(k-1)*C+C-N，然后我们上面的思路不是让两个指针分别从起点和相遇点开始走嘛

begin从起点开始走，meet从相遇点开始走，两人同步走，每次都是走一步。
那begin走了L步走到入环点
meet就也走L步，L又等于(k-1)*C+C-N，即meet先绕环走k-1圈（k>=1)，那meet从入环点开始走的，不论走几圈，只要是整圈，还停下来就还是在相遇点这个位置嘛，然后还要走一个C-N，而我们看图C-N刚好就是相遇点距离入环点的距离。
所以meet走了L（(k-1)*C+C-N）步之后正好也走到了入环点。