【蓝桥杯真题】（一）递归与递推 (Acwing 蓝桥杯笔记)_蓝桥杯过往递推题(2)

最新推荐文章于 2025-01-14 20:26:32 发布

2401_84973592

最新推荐文章于 2025-01-14 20:26:32 发布

阅读量361

点赞数 3

文章标签： c语言 c++ 学习

本文链接：https://blog.youkuaiyun.com/2401_84973592/article/details/138930216

版权

网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。

需要这份系统化的资料的朋友，可以添加戳这里获取

一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！

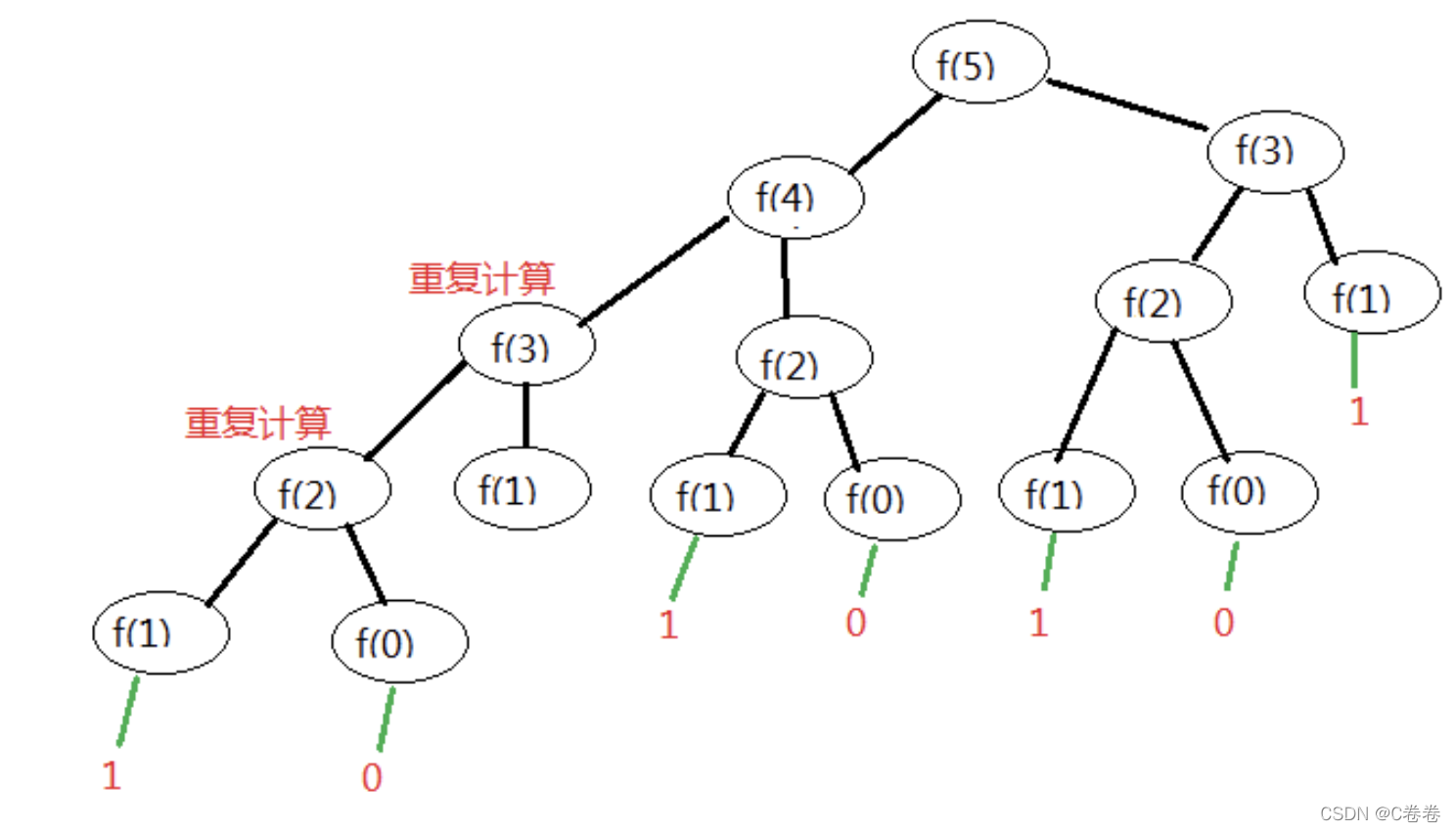
这个数列从第3项开始，每一项都等于前两项之和。

输入一个整数 N，请你输出这个序列的前 N 项。

输入格式
一个整数 N。

输出格式
在一行中输出斐波那契数列的前 N 项，数字之间用空格隔开。

数据范围

0<N<46

输入样例：

5
1
输出样例：

0 1 1 2 3


### 思路一 【递归】


![在这里插入图片描述](https://img-blog.csdnimg.cn/4208316b658a41199b1b4f6cde9ee90e.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAQ-WNt-WNtw==,size_20,color_FFFFFF,t_70,g_se,x_16)

#include
using namespace std;
int dfs(int u) { //从下标为0 开始
if(u == 0) { //第0项
return 0;
}
if (u == 1 || u == 2) { //第1、2项
return 1;
}
if (u > 2) {//第二项之后的
return dfs(u - 1) + dfs(u - 2);
}
}
int main () {
int n;
cin >> n;
for (int i = 0; i < n; i ++) {
cout << dfs(i) << ’ ';
}
return 0;
}


### 思路二 【递推】

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
int n;
cin >> n;
/*普通变量写法，节省空间*/
int a = 0, b = 1;
for (int i = 1; i <= n; i++) {
cout << a << ’ ';
int c = a + b;
a = b;
b = c;
}
/*数组递推
ll f[46];
f[1] = 0, f[2] = 1;
for (int i = 3; i <= n; i++) {
f[i] = f[i - 1] + f[i - 2];
}
for (int i = 1; i <= n; i++) {
cout << f[i] << ’ ';
}
*/
return 0;
}


## 🌟2、Acwing92.递归实现指数型枚举


### 题目描述


[题目链接](https://bbs.youkuaiyun.com/topics/618668825)  
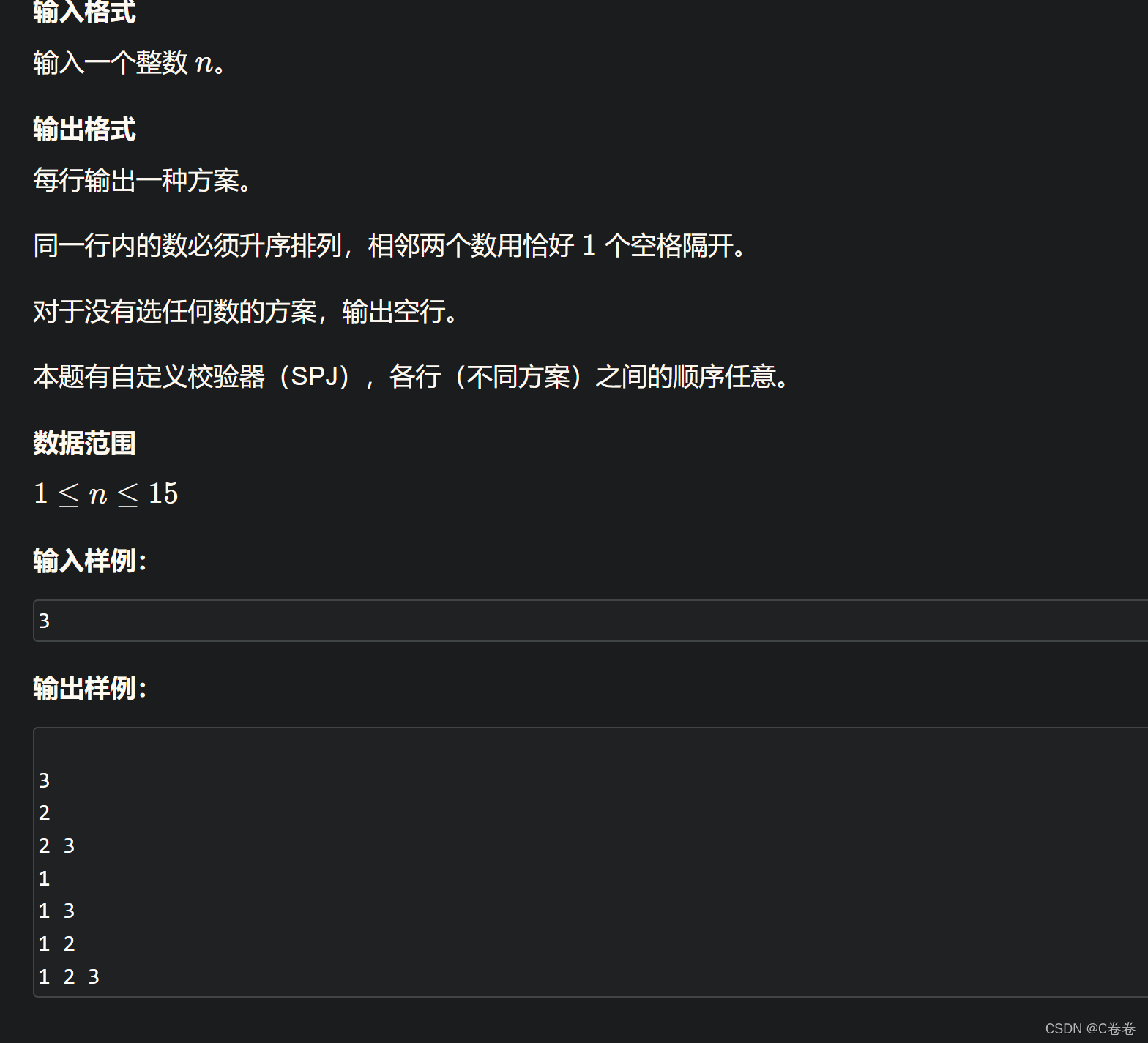
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/5dc786b2a1e246f78d80377f7b7afc55.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAQ-WNt-WNtw==,size_20,color_FFFFFF,t_70,g_se,x_16)


### 思路



> 
> 写出递归搜索树  
>  ![在这里插入图片描述](https://img-blog.csdnimg.cn/87dddb8f64ca40ad999857b0cb209136.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAQ-WNt-WNtw==,size_20,color_FFFFFF,t_70,g_se,x_16)  
>  ![在这里插入图片描述](https://img-blog.csdnimg.cn/73111ac1df6f42ea89250e4711ced2b2.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAQ-WNt-WNtw==,size_20,color_FFFFFF,t_70,g_se,x_16)
> 
> 
> 


### AC代码

#include
#include
#include
using namespace std;
const int N = 16;
int st[N];
int n;
void dfs (int u) {//u ：层数
if (u > n) {//叶子结点
for (int i = 1; i <=n; i ++ ){
if (st[i] == 1) {//如果选了就输出 1选 2不选
cout << i << ’ ';
}
}
puts(“”);
return ;
}

st [u] = 1;//选
dfs (u + 1);//递归下一层
st[u] = 0;//回溯

st[u] = 2;//不选
dfs (u+1);//递归下一层
st[u] = 0;//回溯【恢复现场】

}
/* 写法2
void dfs (int u) {//u ：层数
if (u > n) {//叶子结点
for (int i = 1; i <=n; i ++ ){
if (st[i]) {
cout << i << ’ ';
}
}
puts(“”);
return ;
}
st[u] = true;//选
dfs(u + 1);
st[u] = false;//不选
dfs(u + 1);
}
*/
int main () {
cin >> n;
dfs(1);
return 0;
}


## 🌟3、94. 递归实现排列型枚举


[题目链接](https://bbs.youkuaiyun.com/topics/618668825)  
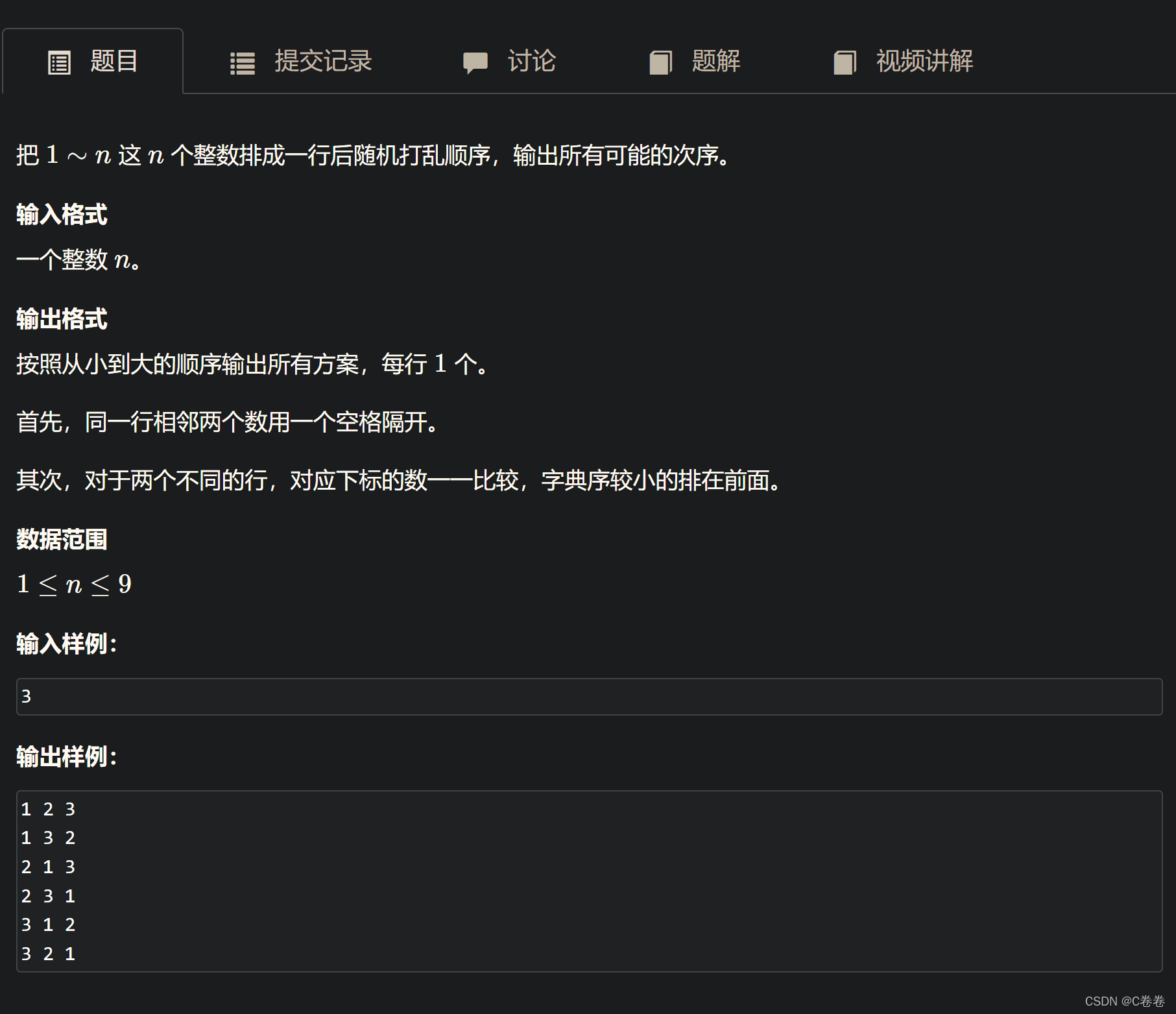
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/f043f27c45e14557bcefdcc0ae628464.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAQ-WNt-WNtw==,size_20,color_FFFFFF,t_70,g_se,x_16)


### 思路


[这篇文章详细一点 DFS 排列数字](https://bbs.youkuaiyun.com/topics/618668825)



> 
> 与排列数组一样 ，其实在枚举的时候，就已经按照字典序递归了。  
>  可以定义一个数组`path[N]` 来保存当前的路径/模拟`DFS`的过程，当这个数组数字填满的时候，就把当前的数字输出出来，然后回溯的时候就需要一个核心操作回溯(恢复现场)
> 
> 
> 


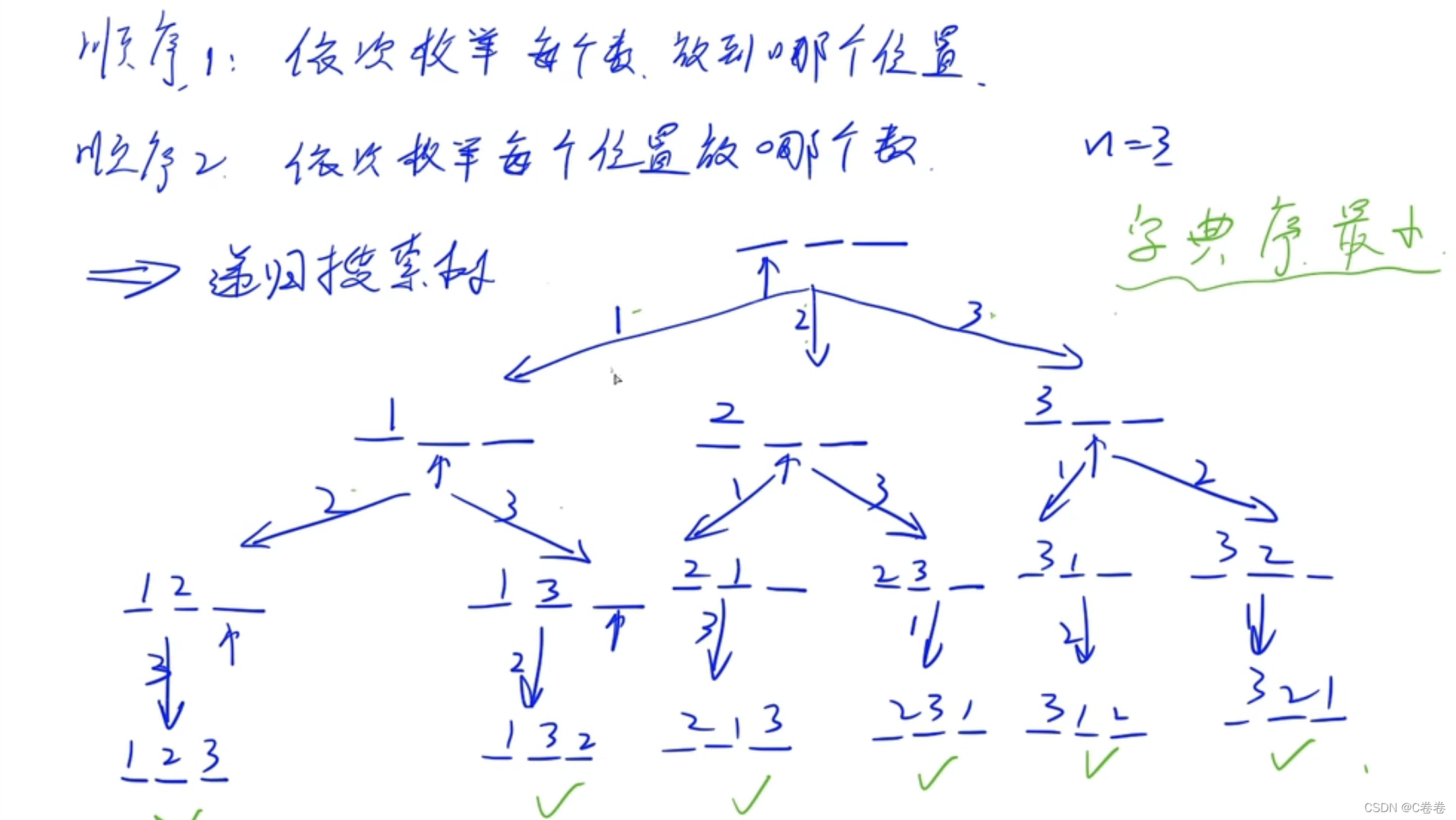
![在这里插入图片描述](https://img-blog.csdnimg.cn/17b607ac652541c38d8e46240f5edc51.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAQ-WNt-WNtw==,size_20,color_FFFFFF,t_70,g_se,x_16)


### AC代码

#include <bits/stdc++.h>
using namespace std;
const int N = 10;
int path[N];
int st[N];
int n ;
void dfs (int u) {
if(u > n) {
for (int i = 1; i <= n; i ++ ) {
cout << path[i] << ’ ';
}
cout << endl;
return;
}
for (int i = 1; i <=n ; i ++ ) { //遍历每一个值
if (!st[i]){
st[i] = 1;
path[u] = i;
dfs (u + 1);
st[i] = 0; //恢复现场
}
}
}
int main () {
cin >> n;
dfs(1);
return 0;
}


## 🌟4、Acwing .93. 递归实现组合型枚举


[题目链接](https://bbs.youkuaiyun.com/topics/618668825)  
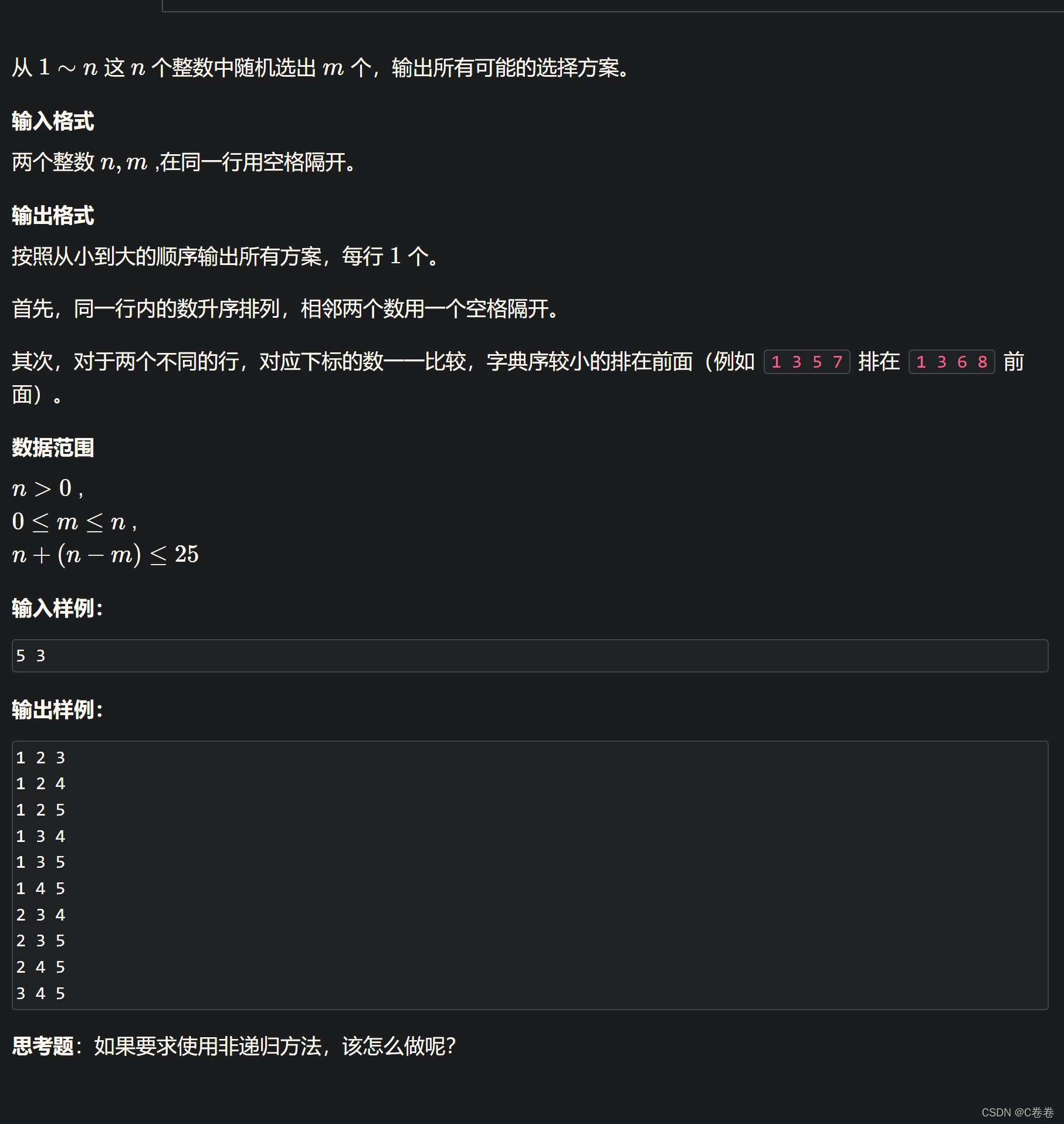
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/fdb4c6cca3724e6f806366d95644bf32.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAQ-WNt-WNtw==,size_20,color_FFFFFF,t_70,g_se,x_16)


### 思路



> 
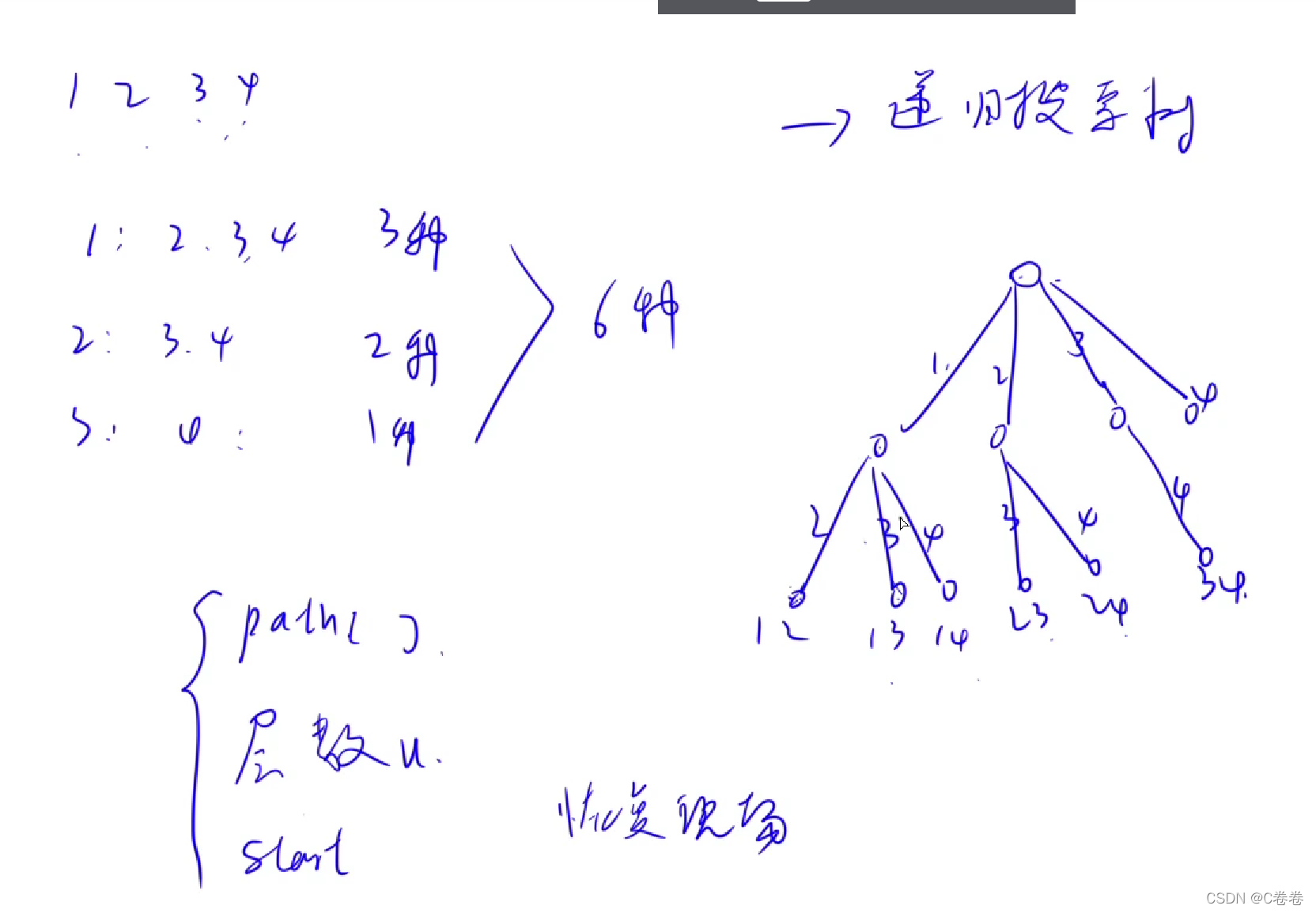
> 与上道题类似，只是细节上发生了一点小变化  
>  ![在这里插入图片描述](https://img-blog.csdnimg.cn/97ed368a102e4080b9a8e05cb040e048.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAQ-WNt-WNtw==,size_20,color_FFFFFF,t_70,g_se,x_16)
> 
> 
> 


### AC代码

#include <bits/stdc++.h>
using namespace std;
const int N = 30;
int path[N];
int n, m;

void dfs (int u, int start ) {//u:层数 start：起始的数值
if (u > m) {
for (int i = 1; i <= m; i ++ ) {
cout << path[i] << ’ ';
}
puts(“”);
}
else {
for (int i = start; i <= n; i ++) {//
path[u] = i;//表示已经填了
dfs(u + 1, i + 1);//递归下一层
path[u] = 0;//恢复现场
}
}
}

int main () {
cin >> n >> m;
dfs(1,1); //第一层开始且从1开始枚举
return 0;
}


## 🌟5、Awing95. 费解的开关


[题目太长了 点链接看](https://bbs.youkuaiyun.com/topics/618668825)  
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/16060244d06b4e9686136d560b0d015a.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAQ-WNt-WNtw==,size_20,color_FFFFFF,t_70,g_se,x_16)


### 思路 【类似八数码】


* 位运算（开关 `^1`即可） + 递推
* 每一个位置最多只会操作一次。操作两次==不操作，自然就不可能是最优解。
* 递推的时候：第一行是不可以按的，第一行的要按的格子，确定了第二行要按的相应位置。换句话说，只能从下一行去改变上一行的灯的状态。
* 最后一行是不能按的。【因为它的上面行已经全是1了，我们就无法修改最后一行了】  
 ![在这里插入图片描述](https://img-blog.csdnimg.cn/611d55b0227d458c878efdaaed6d14c5.png)


### AC代码

#include <bits/stdc++.h>
using namespace std ;
const int N = 7;
char g[N][N];
int m;//取无穷并不影响最大值

void open(int x, int y) {
int dx[5] = {0, -1, 0, 1, 0}, dy[5] = {0, 0, 1, 0, -1};//分别对应本位右下左上
for (int i = 0; i < 5; i ++) {
int a = x + dx[i], b = y + dy[i];
if(a>=0 && a<5 && b>=0 && b<5) {//判断是否在5x5内
g[a][b] ^= 1;//异或同 0 异1
}
}
}

int work() {
int ans = 1e8;
for (int k = 0; k < 32; k ++) {//枚举第一行所以按法
int cnt =0; //cnt要写for里面教训！！！
char tmp[10][10];//储存g
memcpy(tmp,g,sizeof g);//copy g —> tmp

	for (int j = 0; j < 5; j ++) {  // <<优先级高于 &(只有1&1 == 1) 
		if ((k >> j) & 1) {  //位运算 举例12和2 二进制分别是 
			cnt ++;			// 01100 和 00010 
			open (0,j);		//按第4、3位 按第2位 
		} 					 
	}
	
	//根据第一行 递推前四行 
	for (int i = 0; i < 4; i ++) {
		for (int j = 0; j < 5; j ++) {
			if(g[i][j] == '0') {
				cnt ++;
				open(i + 1, j);
			} 
		}
	}
	
	//判断最后一行是否全为1
	bool is_successful = true;
	for(int j = 0; j < 5; j ++) {
		if(g[4][j] == '0') {
			is_successful = false;
			break;
		} 
	}
	
	if(is_successful) {
		ans = min(ans,cnt);
	}
	
	memcpy(g,tmp,sizeof g);//恢复原状 
}

if(ans > 6) {
ans = -1;
}
return ans;
}

int main () {
cin >> m;
while ( m --) {
for (int i = 0; i < 5; i ++) {
cin >> g[i];
}
cout << work() << endl;
}
return 0;
}


## 🌟6、带分数


[题目链接](https://bbs.youkuaiyun.com/topics/618668825)


### 思路



> 
> dfs的排列数字 ①枚举a ②枚举c ③判断a c  
>  `n = a + b/c` & `b= n*c - a*c`
> 
> 
> 


### AC代码

#include <bits/stdc++.h>
using namespace std;
int ans = 0;
const int N = 520;
int had_use[N],ever[N];
int n;

bool check(int a,int c){
int b = n*c - a*c;
if(!a||!b||!c) return false; //如果有一个数为0
memcpy(ever,had_use,sizeof had_use);//用来判断且不会改变原数组的目的
while (b) {
int t = b % 10;//取个位
b /= 10; //删除
if(!t ||ever[t]) return false;
ever[t] = 1;
}
for (int i = 1; i <= 9; i ++) {
if(!ever[i]) {
return false;//判断1-9是否都已经用了
}
}