

既有适合小白学习的零基础资料,也有适合3年以上经验的小伙伴深入学习提升的进阶课程,涵盖了95%以上Go语言开发知识点,真正体系化!
由于文件比较多,这里只是将部分目录截图出来,全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频,并且后续会持续更新
printf("最长子序列的个数为: %d", ans);
return 0;
}
/*
样例:
7
7 9 6 10 7 1 3
最长子序列的个数为: 3
*/
这样就完了吗?如果这样就完了就不叫详解啦~ 一会会慢慢讲,它的优化还有他的标记路径的方法。
先歇会,既然学了就来几道模板提练练手把!(都会有题解哒,先自己来一边试试!)
[https://vjudge.net/contest/218661#problem/A](https://bbs.youkuaiyun.com/topics/618658159)
改题目为一个模板题,直接求解最长上升子序列即可
AC代码:
//https://vjudge.net/contest/218661#problem/A
#include
#include
#include
using namespace std;
int main()
{
int n, arr[1005], ans = -1, dp[1005];
scanf(“%d”, &n);
for(int i = 1; i <= n; i++)
scanf(“%d”, &arr[i]);
for(int i = 1; i <=n; i++){
dp[i] = 1;
for(int j = 1; j < i; j++){
if(arr[j] < arr[i])
dp[i] = max(dp[i], dp[j] + 1);
}
ans = max(dp[i], ans);
}
printf(“%d”, ans);
return 0;
}
[[kuangbin带你飞]专题十二 基础DP1 [Cloned] - Virtual Judge](https://bbs.youkuaiyun.com/topics/618658159)
该题也是模板题,直接上代码:
#include
#include
#include
#include
using namespace std;
int dp[1005], n, MAX;
int arr[1005];
int main()
{
while(scanf(“%d”, &n) != EOF){
if(n == 0) break;
MAX = -1;
for(int i = 0; i < n; i++) scanf(“%d”, &arr[i]);
for(int i = 0; i < n; i++){
dp[i] = arr[i];
for(int j = 0 ; j < i; j++){
if(dp[i] < dp[j] + arr[i] && arr[i] > arr[j]){
dp[i] = dp[j] + arr[i];
}
MAX = max(dp[i], MAX);
}
}
printf(“%d\n”, MAX);
}
return 0;
}
写着写着突然发现Vjudge又蹦了。。。 又从洛谷上找的题目,后续可能会再加上几个Vjudge的题目
[[NOIP2004 提高组] 合唱队形 - 洛谷](https://bbs.youkuaiyun.com/topics/618658159)
### 题目描述
NNN 位同学站成一排,音乐老师要请其中的( N−KN-KN−K )位同学出列,使得剩下的 KKK 位同学排成合唱队形。
合唱队形是指这样的一种队形:设K位同学从左到右依次编号为 1,2,…,K1,2,…,K1,2,…,K ,他们的身高分别为 T1,T2,…,TKT\_1,T\_2,…,T\_KT1,T2,…,TK , 则他们的身高满足 T1<...<Ti>Ti+1>…>TK(1≤i≤K)T\_1<...<T\_i>T\_{i+1}>…>T\_K(1 \le i \le K)T1<...<Ti>Ti+1>…>TK(1≤i≤K) 。
你的任务是,已知所有N位同学的身高,计算最少需要几位同学出列,可以使得剩下的同学排成合唱队形。
### 输入输出格式
**输入格式:**
共二行。
第一行是一个整数 N(2≤N≤100)N(2 \le N \le 100)N(2≤N≤100) ,表示同学的总数。
第二行有 nnn 个整数,用空格分隔,第 iii 个整数 Ti(130≤Ti≤230)T\_i(130 \le T\_i \le 230)Ti(130≤Ti≤230) 是第 iii 位同学的身高(厘米)。
**输出格式:**
一个整数,最少需要几位同学出列。
Sample input :
8
186 186 150 200 160 130 197 220
Sample output :
4
题解:他的意思就是说想尽可能的留下学生。而且身高是中间高两边低的,那么如果说最高的要是在最左边,那么直接求他的最长上升子序列就够了,如果说在左边,那么直接从右边求他的最长上升子序列就够了,但是呢不确定最高的在哪里最合适。
现在关键 只要确定了最高的那个,求他的从最左边的最长上升子序列和他从最右边的最长升降子序列,这样就可以保证留下的人数最多,换句话地说就是剔除的人数最少。设dp\_1[ i ] 为从左边上升第 i 个学生的最高上升的个数, dp\_2[ n - i ] 为从右边上降第 i 个学生的最高上升的个数,求和 dp\_3[ i ] = dp\_1[ i ] + dp\_2[ i ] 那么最大的 dp\_3[ i ] ,以这个为终点左边依次低,右边也依次低, 那么最多留下人数就是 dp\_3[ i ] - 1
减去他自己重复了两遍的
栗子:
序号 i : 1 2 3 4 5 6 7 8
身高 186 186 150 200 160 130 197 220
从左边上升dp\_1[ i ] = 1 1 1 2 2 1 3 3
从右边上降dp\_2[ i ] = 4 4 2 3 2 1 1 1
总和dp\_3[ i ] = 5 5 3 5 4 2 4 4
为了保证中间的左边的尽可能多,右边的也尽可能多,所以选择 总和 dp\_3[ i ] 最大的 这里就是 当i == 1 || i == 2 || i == 4的时候 dp\_3[ i ] - 1 == 4 (减去他自己重复的一遍), 所以答案是 8 - 4 == 4 , 因为减去留下的最多的,就是答案咯~
AC代码:
#include
#include
#include
#include
using namespace std;
int main()
{
int N, arr[105], dp[105] = {0}, dp2[105] = {0}, dp_all[105] = {0};
scanf(“%d”, &N);
for(int i = 0; i < N; i++) scanf(“%d”, &arr[i]);
for(int i = 0; i < N; i++){ //求最长上升子序列
dp[i] = 1;
for(int j = 0; j < i; j++){
if(arr[j] < arr[i] && dp[i] < dp[j] + 1)
dp[i] = dp[j] + 1;
}
}
for(int i = N - 1; i >= 0; i–){ //从后往前求最长上升子序列
dp2[i] = 1;
for(int j = N - 1; j > i; j–){
if(arr[j] < arr[i] && dp2[i] < dp2[j] + 1)
dp2[i] = dp2[j] + 1;
}
}
int MAX = -1;
for(int i = 0; i < N; i++){
dp_all[i] = dp[i] + dp2[i];
MAX = max(MAX, dp_all[i]);
}
printf(“%d”, N - MAX + 1);
return 0;
}
LIS的nlogn的优化:
LIS的优化说白了其实是贪心算法,比如说让你求一个最长上升子序列把,一起走一遍。
比如说(4, 2, 3, 1, 2,3,5)这个序列,求他的最长上升子序列,那么来看,如果求最长的上升序列,那么按照贪心,应该最可能的让该序列的元素整体变小,以便可以加入更多的元素。
现在开辟一个新的数组,arr[ 10 ], { .......} --> 这个是他的空间 ,现在开始模拟贪心算法求解最长上升子序列,第一个数是4,先加进去,那么为{ 4 }再来看下一个数2,它比4小,所以如果他与4替换是不是可以让目前子序列(他这一个元素组成的子序列)变得更小,更方便以后元素的加入呢?是的 。同时还保证了序列的长度不变,所以将大的数替换成小的是可以在保证序列长度不变的前提下是整体序列更小,更容易加入元素 。所以现在为{ 2 } 再来看他的下一个元素3,他要比2大,所以呢加在他的后面,{ 2, 3}
再看下一个元素是1,它比3要小,所以呢为了保证子序列整体尽可能的小(以便可以加入更多的元素),从目前的序列中查找出第一个比他大的数替换掉,那么就变成了{ 1, 3},继续。。 下一个数是2,那么序列变为{ 1,2},再下一个数为3,那么序列为{1,2,3},在下一个数为5,那么序列为{1,2,3,5},完。 目前序列里又4个元素,所以他的最长子序列的个数为4,但是这个序列是一个伪序列,里面的元素,并不是真正的最长上升子序列,而仅仅和最长上升子序列的个数一样。因为查找的时候用的二分查找,所以时间复杂度为o(nlogn)。
实现代码:
#include
#include
#include
using namespace std;
int main()
{
int arr[500], n, dp[500], ans = -1;
scanf(“%d”, &n);
for(int i = 1; i <= n; i++)
scanf(“%d”, &arr[i]);
/* 求解最长子序列的个数的核心代码 /
/ ********************************************** */
int k = 1;
dp[k] = arr[1];
for(int i = 2; i <= n; i++){
if(dp[k] < arr[i]) dp[++k] = arr[i]; //如果比最后一个元素大,那么就添加再最后末尾处
else (lower_bound(dp + 1, dp + 1 + k, arr[i])) = arr[i]; //如果比最后一个元素小,那么就替换该序列第一个比他大的数;
}
/ ********************************************** */
printf("最长子序列的个数为: %d", k);
return 0;
}
标记路径:
O(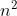)算法标记路径,只需要使用一个记录前驱的数组 pre 即可。
还是用刚才的序列:(7, 9, 6, 10, 7, 1, 3)分别为 (a1, a2, a3, a4, a5, a6, a7)
最开始a1 = 7, 令dp[ 1 ] = 1, pre[1] = 1;
然后看下一个元素 a2 = 9, 令dp[ 2 ] = 1, pre[2] = 2, 那么需要检查 i 前面是否有比他小的 因为 a1 < a2 而且 dp[ 1 ] + 1 > dp[ 2 ], 所以dp[ 2 ] = dp[ 1 ] + 1 == 2,同时更新标记 pre[2] = 1;
然后再看下一个元素 a3 = 6, 令 dp[ 3 ] = 1, pre[3] = 3, 那么需要检查前面的元素 a1 与 a2 是否有比他小的, 一看没有,辣么 到目前为止,子序列就是他自己。
然后再看一下下一个元素 a4 = 10; 令 dp[ 4 ] = 1, pre[4] = 4; 那么需要依次检查前面的元素 a1 与 a2 与 a3 是否有比他小的 , 一看a1比它小,而且呢,dp[ 1 ] + 1 > dp[ 4 ] 所以呢 dp[ 4 ] = dp[ 1 ] + 1 == 2, pre[4] = 1, 说明此时 a1 与 a4 可以构成一个长度为 2 的上升子序列,再来看看还可不可以构成更长的子序列呢,所以咱们再来看看 a2 , a2 < a4 而且呢 dp[ 2 ] + 1 == 3 > dp[ 4 ] == 2 所以呢dp[ 4 ] = dp[ 2 ] + 1 == 3, pre[4] = 2, 即将a4承接在a2后面比承接在a1后更好,承接在a2后面的序列为:a1 a2 a4 ,构成一个长度为 3 的上升子序列; 然后再来看 a3 , a3 < a4 但是可惜的是 d[ 3 ] + 1 == 2 < dp[ 4 ] == 3 , 所以呢就不能把a4加在a3的后面 。
然后就是重复上述过程,更新完所有的pre。
dp 1 2 1 3 2 1 2
pre 1 1 3 2 3 6 6
最大的 dp 值为 3,所以最长子序列长度为3, 末尾的元素在4位置。
追踪其路径为:4 -> pre[4] == 2 -> pre[2] == 1 -> pre[1] == 1(停止) 路径为 4,2,1,这个为倒叙的,因为从后往前找的。
题目连接:[http://acm.hdu.edu.cn/showproblem.php?pid=1160](https://bbs.youkuaiyun.com/topics/618658159) 一种经典的LIS路径标记的题目。
题意:给出n只老鼠 。每只老鼠有对应的weight 和 speed。现在需要从这 n 只老鼠的序列中,找出最长的一条序列,满足老鼠的weight严格递增,speed严格递减,数据中可能有 weight 和 speed 都相同的老鼠。
题解:我们先按照 speed 递减排序,剩下的只需要找 weight 的严格递增的子序列就可以,这么就转化为求最长上升子序列的问题了。
#include<bits/stdc++.h>
#define up(i, x, y) for(ll i = x; i <= y; i++)
#define down(i, x, y) for(ll i = x; i >= y; i–)
#define bug printf(“***************************\n”)
#define debug(x) cout<<#x"=[“<<x<<”]" <<endl
#define IO ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
#define lk k<<1
#define rk k<<1|1
typedef long long ll;
typedef unsigned long long ull;
const double eps = 1e-8;
const ll mod = 1e9 + 7;
const ll maxn = 1e5 + 7;
const double pi = acos(-1);
const ll inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3fLL;
using namespace std;
int cnt, ans, loc, x, y;
int dp[maxn], pre[maxn], path[maxn];
struct node
{
int w, v, id;
}a[maxn];
bool cmp(node a, node b)
{
if(a.v != b.v)
return a.v > b.v;
return a.w < b.w;
}
int main(int argc, char const *argv[])
{
while(cin >> x >> y)
{
a[++cnt].w = x;
a[cnt].v = y;
a[cnt].id = cnt;
}
sort(a + 1, a + 1 + cnt, cmp);
for(int i = 1; i <= cnt; ++i)
{
dp[i] = 1;
pre[i] = i; // 初始化,自己一个元素作为子序列,那么自己的前驱节点就是自己了
for(int j = 1; j < i; ++j)
{
if(a[j].w < a[i].w && dp[i] < dp[j] + 1 && a[j].v != a[i].v)
//1. 满足w的单调严格递增 2. 可以更新 3.由于速度是严格单调递减的,所以加上 dp[j].v != d[i].v 这个条件
{
dp[i] = dp[j] + 1; // 当前的序列是 ai 承接在 aj 之后,所以 ai 的前驱节点是 j 节点
pre[i] = j; // 更改前驱节点
}
if(ans < dp[i]) // 更新记录的最长子序列的长度,以及最长子序列末尾元素的位置
{
ans = dp[i]; // 更新记录的最长子序列的长度
loc = i; // 更新最长子序列末尾元素的位置,为了方便输出路径
}
}
}
for(int i = 1; i <= ans; i++)
{
path[i] = a[loc].id; // 需要记录原来的真实位置,所以给path赋的是 id, 不是loc
loc = pre[loc]; // 根据记录的前驱数组来查找
}// 这里的路径是从后往前的,输出的时候注意需要反过来
printf("%d\n", ans);
for(int i = ans; i >= 1; i--)
{
printf("%d\n", path[i]);
}
return 0;
}
nlogn 算法的路径标记:
首先要明确的是通过nlogn算法得到的最后的序列是乱的,只有序列的长度是有价值的,所以最后的序列并不是路径。不过我们可以对更新过程中的实际位置来进行标记,最后得到想要的路径。直接举例子吧。用mp数组记录在序列中的位置。
比如说(4, 2, 3, 1, 2,3,5)这个序列,求他的最长上升子序列,那么来看,如果求最长的上升序列,那么按照贪心,应该最可能的让该序列的元素整体变小,以便可以加入更多的元素。
现在开辟一个新的数组,arr[ 10 ], { .......} --> 这个是他的空间 ,现在开始模拟贪心算法求解最长上升子序列,第一个数是4,先加进去,那么为{ 4 },并且这时候 mp[1] = 1,因为a1在序列中是在第一个位置,所以mp[1] = 1。再来看下一个数2,它比4小,所以如果他与4替换是不是可以让目前子序列(他这一个元素组成的子序列)变得更小,更方便以后元素的加入呢?是的。所以现在为{ 2 } 并且这时候 mp[2] = 1,因为a2在序列中仍然是在第一个位置,所以mp[2] = 1。再来看他的下一个元素3,他要比2大,所以呢加在他的后面,{ 2, 3} 并且这时候 mp[3] = 2,因为a2在序列中是在第2个位置,所以mp[3] = 2。
再看下一个元素是1,它比3要小,所以呢为了保证子序列整体尽可能的小(以便可以加入更多的元素),从目前的序列中查找出第一个比他大的数替换掉,那么就变成了{ 1, 3} 并且这时候 mp[4] = 1,因为a4在序列中是在第一个位置,所以mp[4] = 1,继续。下一个数是2,那么序列变为{ 1,2}并且这时候 mp[5] = 2,因为a5在序列中是在第2个位置,所以mp[5] = 2,再下一个数为3,那么序列为{1,2,3}并且这时候 mp[6] = 3,因为a6在序列中是在第3个位置,所以mp[6] = 3,在下一个数为5,那么序列为{1,2,3,5}并且这时候 mp[7] = 4,因为a7在序列中是在第4个位置,所以mp[7] = 4,完。 目前序列里又4个元素,所以他的最长子序列的个数为4,但是这个序列是一个伪序列,里面的元素,并不是真正的最长上升子序列,而仅仅和最长上升子序列的个数一样。因为查找的时候用的二分查找,所以时间复杂度为o(nlogn)。
序列 : 4, 2, 3, 1, 2, 3, 5
mp: 1 1 2 1 2 3 4
// 所以从最右边往左边找即可:
for(int i = n; i >= 1; i–)
{
if(mp[i] == top) // top 是最长子序列的长度
path[top–] = i; // path 记录的路径
}
// 在这里路径为: 4 5 6 7
题目连接:[http://acm.hdu.edu.cn/showproblem.php?pid=1160](https://bbs.youkuaiyun.com/topics/618658159) 和上面的例题一样只是做法用的 nlogn 的算法。
#include<bits/stdc++.h>
#define up(i, x, y) for(ll i = x; i <= y; i++)
#define down(i, x, y) for(ll i = x; i >= y; i–)
#define bug printf(“***************************\n”)
#define debug(x) cout<<#x"=[“<<x<<”]" <<endl
#define IO ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
#define lk k<<1
#define rk k<<1|1
typedef long long ll;
typedef unsigned long long ull;
const double eps = 1e-8;
const ll mod = 1e9 + 7;
const ll maxn = 1e5 + 7;
const double pi = acos(-1);
const ll inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3fLL;
using namespace std;
int top, ans, len, x, y;
int st[maxn], mp[maxn], path[maxn];
struct node
{
int w, v, id;
}a[maxn];
bool cmp(node a, node b)
{
if(a.v != b.v)
return a.v > b.v;
return a.w < b.w;
}
int main(int argc, char const *argv[])
{
while(cin >> x >> y)
{
a[++len].w = x;
a[len].v = y;
a[len].id = len;
}
sort(a + 1, a + 1 + len, cmp);
top = 0;
st[++top] = a[1].w; // 将第一个元素压入栈中
mp[a[1].id] = 1; // 确定第一个元素的位置
for(int i = 2; i <= len; ++i)
{
if(a[i].w > st[top]) // 如果当前的值大于栈顶的元素
{
st[++top] = a[i].w; // 加入栈中



既有适合小白学习的零基础资料,也有适合3年以上经验的小伙伴深入学习提升的进阶课程,涵盖了95%以上Go语言开发知识点,真正体系化!
由于文件比较多,这里只是将部分目录截图出来,全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频,并且后续会持续更新
(int i = 2; i <= len; ++i)
{
if(a[i].w > st[top]) // 如果当前的值大于栈顶的元素
{
st[++top] = a[i].w; // 加入栈中
[外链图片转存中…(img-IZwCqUqK-1715832021303)]
[外链图片转存中…(img-dULgFzmf-1715832021303)]
[外链图片转存中…(img-zPtI3YMX-1715832021303)]
既有适合小白学习的零基础资料,也有适合3年以上经验的小伙伴深入学习提升的进阶课程,涵盖了95%以上Go语言开发知识点,真正体系化!
由于文件比较多,这里只是将部分目录截图出来,全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频,并且后续会持续更新
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








