介绍
LIS 问题即最长递增子序列(Longest Increasing Subsequence)问题,是计算机科学和算法领域中的经典问题,以下从定义、求解方法等方面详细介绍:
子序列:
设(S = {a_1, a_2, a_3, ....... a_n})是一个给定的序列,(S')是由(S)中的若干个元素按照它们在(S)中的相对顺序排列而成的序列,则称(S')是(S)的一个子序列。例如,对于序列\(S = [1, 3, 5, 7, 9]\),它的子序列可以是([1, 5, 9])、([3, 7])、([1, 9])等,甚至单个元素如([1])、([7])也可以看作是它的子序列。
LIS定义:
给定一个长度为 (n) 的序列 (a_1,a_2........,a_n),找出其中一个递增子序列(即子序列中的元素按照从小到大的顺序排列),使得该子序列的长度最长,这个最长的递增子序列的长度就是 LIS 问题的解。例如对于序列 ([1, 3, 2, 4, 6, 5]),它的一个最长递增子序列是 ([1, 3, 4, 6]),长度为 (4)。
引例:
![]()
1,使用暴力做法,每一个数都有选和不选这两个情况,所以我们可以进行深度搜索,对递增的子序列进行查找,但是这样的时间复杂度太高,2^n,不是很理想
2,使用动态规划法,
第一步,我们将f[i]记录为以i结尾的最长序列的长度
第二步,每次的f[i],只能从前i-1个地方转移过来,所以需要遍历前i-1来选择其中最优的来转移
伪代码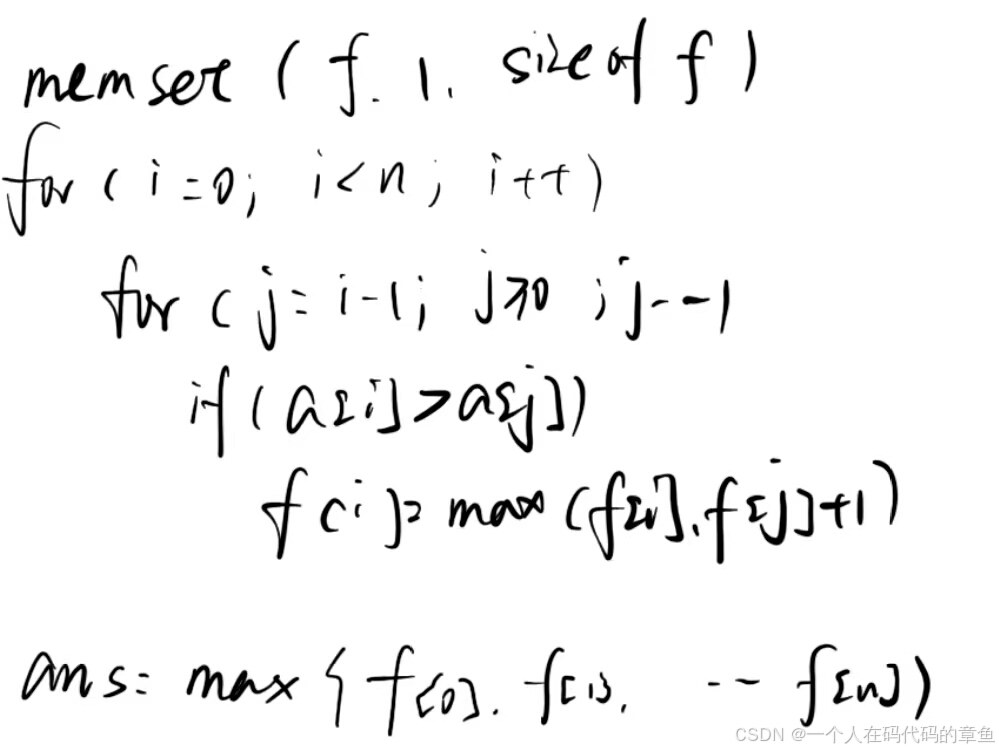
习题1

分析
这是一道基于动漫角色设定的算法逻辑题。以《名侦探柯南》中的怪盗基德为背景,讲述怪盗基德偷走钻石后,伪装被柯南识破,滑翔翼动力装置也遭破坏,只能操控受损滑翔翼逃脱。设定城市有(N)幢高度各异且排成一线的建筑,基德初始可在任意一幢建筑顶端,选一个方向逃跑且不能中途改变,因滑翔翼受损只能从高建筑向低建筑滑行。问题是求他最多能经过多少幢不同建筑的顶部(含初始建筑),本质是求最长下降子序列的长度问题。
根据题目意思分析,让我们求的是从左到右的最长上升子序列和从右到左的最长上升子序列中最长的那个的长度
伪代码如下:
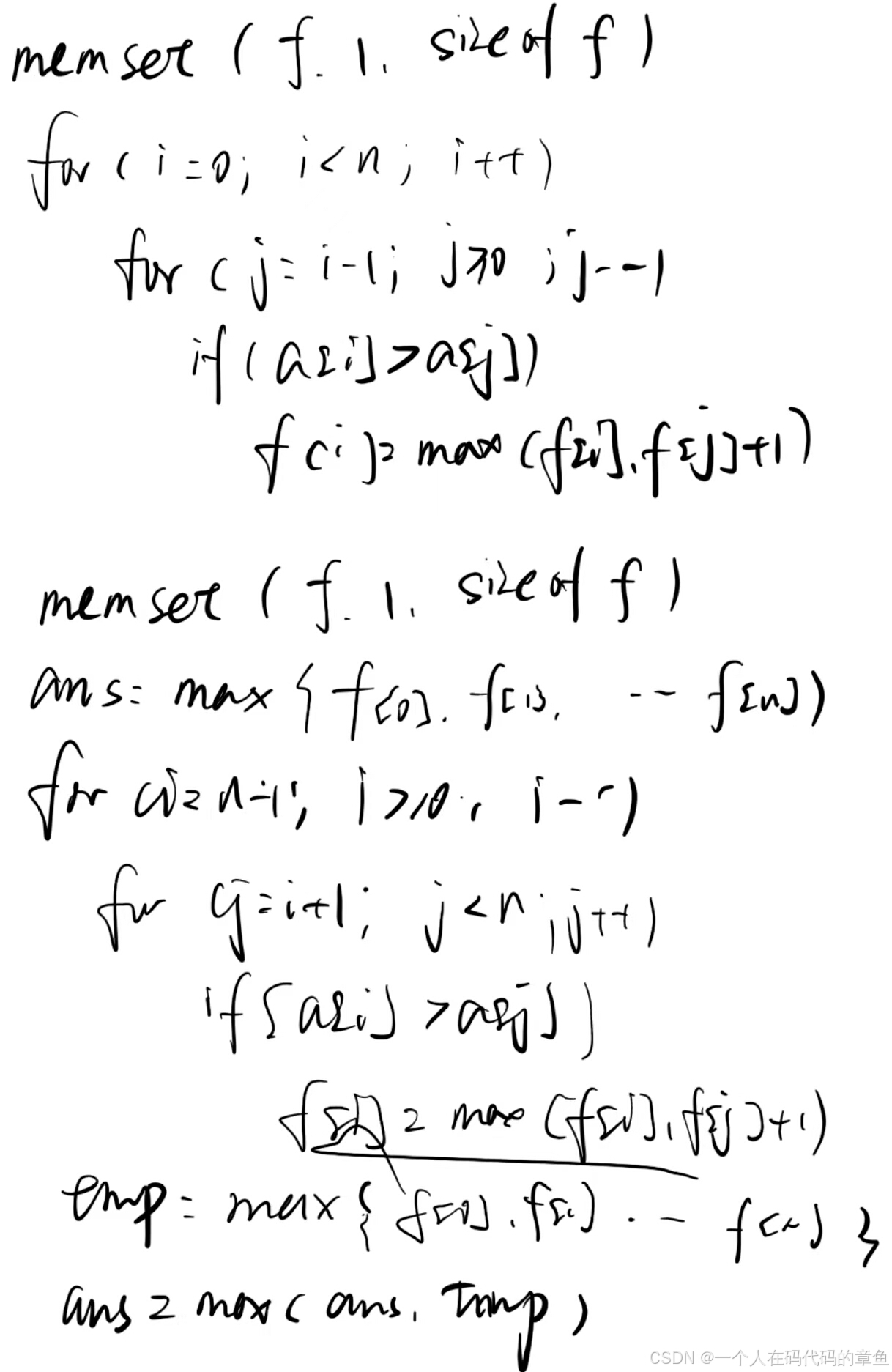
习题2

分析:
这是一道结合实际场景的算法问题。ACM 队在五一登山观光,山上有\(N\)个按顺序排列的景点,队员需按编号递增顺序浏览。同时,遵循不连续浏览海拔相同景点,且开始下山后不再上山的登山习惯。目标是在满足这些条件下,求出最多可浏览的景点数。从算法角度看,这是一个寻找满足特定条件的最长序列问题,涉及对景点编号和海拔高度两个维度条件的综合考量,需要运用合适的算法策略,
来求解符合条件的最长景点浏览序列长度。
题目描述的条件就是:1,相邻的两个景点不能相同海拔,2一旦海拔下降就不会上升了
很像一个山形的路线,让我们找到一个可以浏览最多的景点。如果直接去想要浏览哪些景点似乎有一点困难,不如我们直接去思考如何选择山头(什么时候向下走),因为我们可以很轻松的知道如何求出一个点到起点和终点的最长上升/下降子序列,如果一个点的左边的最长上升子序列的长度+右边的最长下降子序列的长度最长,那么我们就可以确定在这个点时我们要下降。伪代码如下
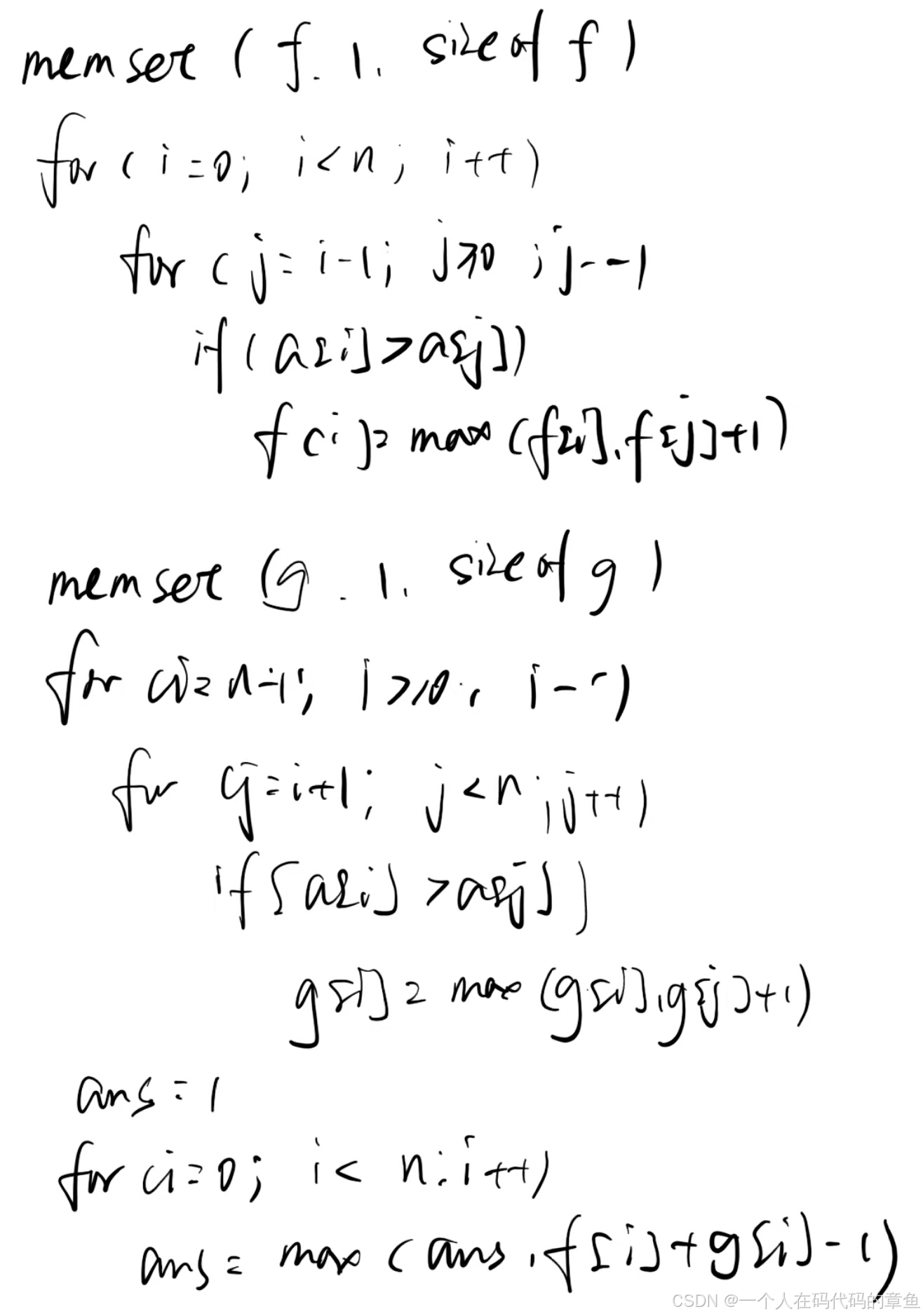
习题3:

分析:
这道题目和上一题如出一辙,但是一个是求的最长的像山形的序列,这里让我们求的是,要请出来几个同学,才能变成山形。其实就是求出最长的山形序列m,然后让总长度-山形序列长度
伪代码如下:
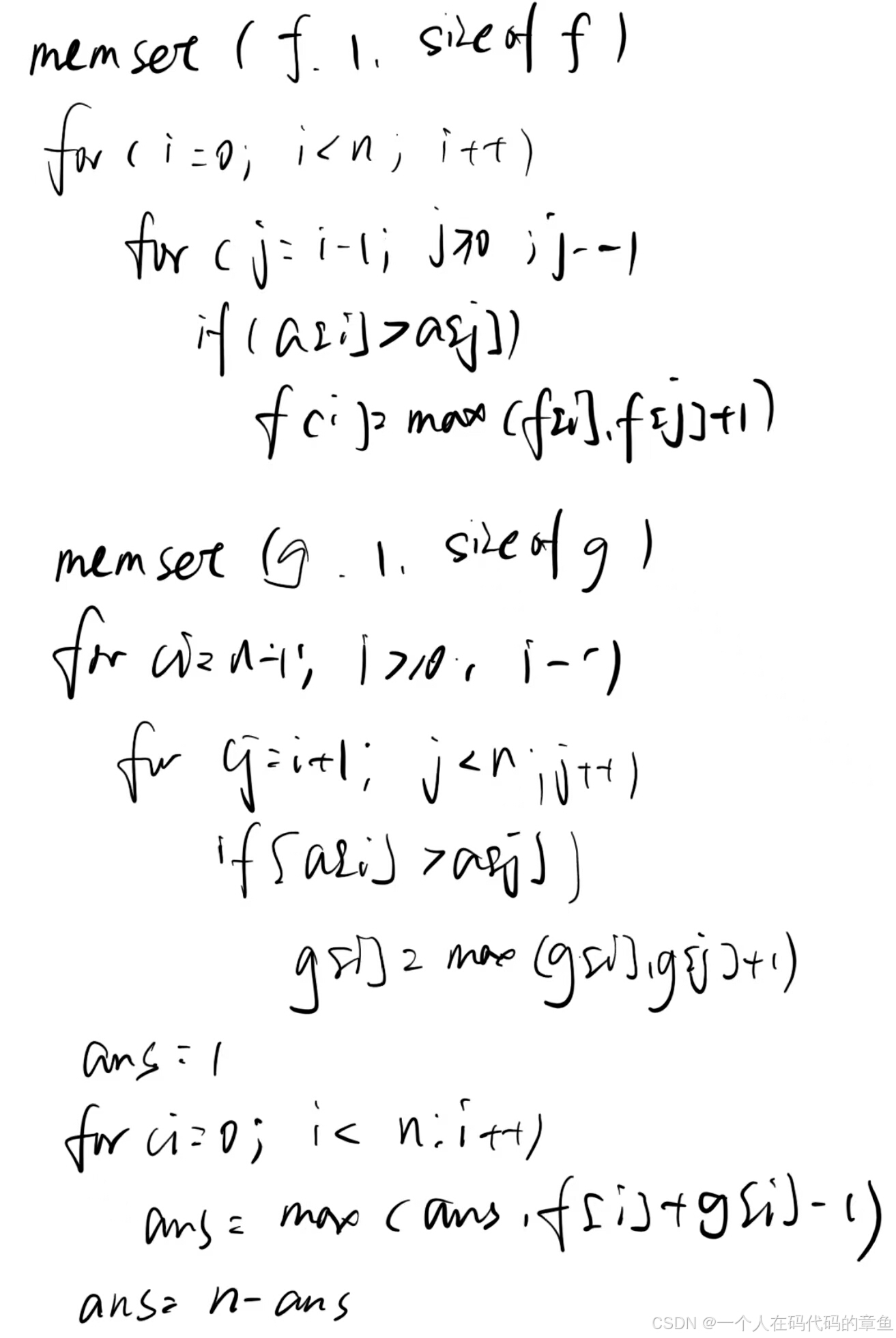
习题4:

分析
这是一道以城市航线规划为背景的算法类题目。在 Palmia 国,有一条横贯东西的大河,其笔直的南北两岸各分布着\(N\)个位置互异的城市。北岸每个城市在南岸有且仅有一个友好城市,且不同北岸城市对应的南岸友好城市各不相同。每对友好城市都申请在河上开辟直线航道相连,但因河上雾大,政府为避免事故,决定不允许任意两条航道交叉。题目要求通过编程帮助政府做出批准或拒绝申请的决策,目标是在保证任意两条航线不相交的前提下,使获批的申请数量尽可能多。
题目的意思如下:
我们分为上下两边,我们以下侧为我们的主参考,如果我们把下面的友好城市情况写成数组的形式
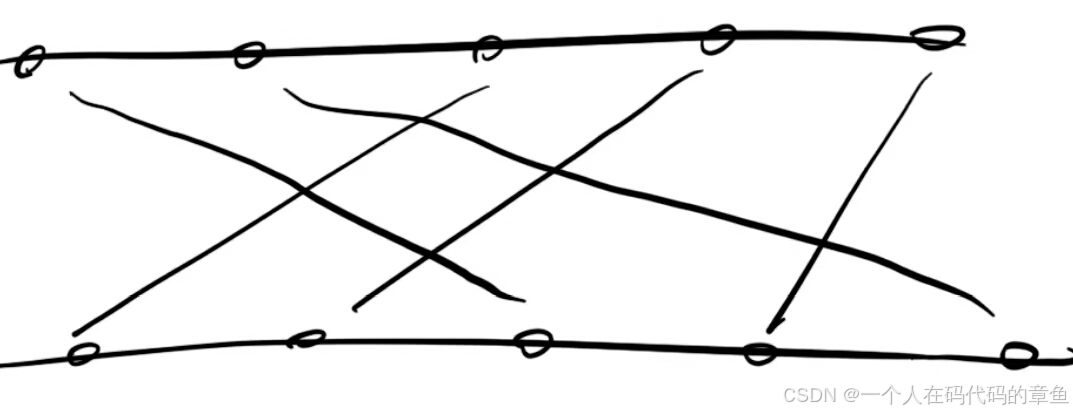
(3,4,1,5,2)
最多审批的桥数是3,分别是1-3,2-4,4-5
我们发现这就是我们这个数组的最长上升子序列,所以这道题就是一个最长上升子序列的另外一种表现形式
伪代码如下:
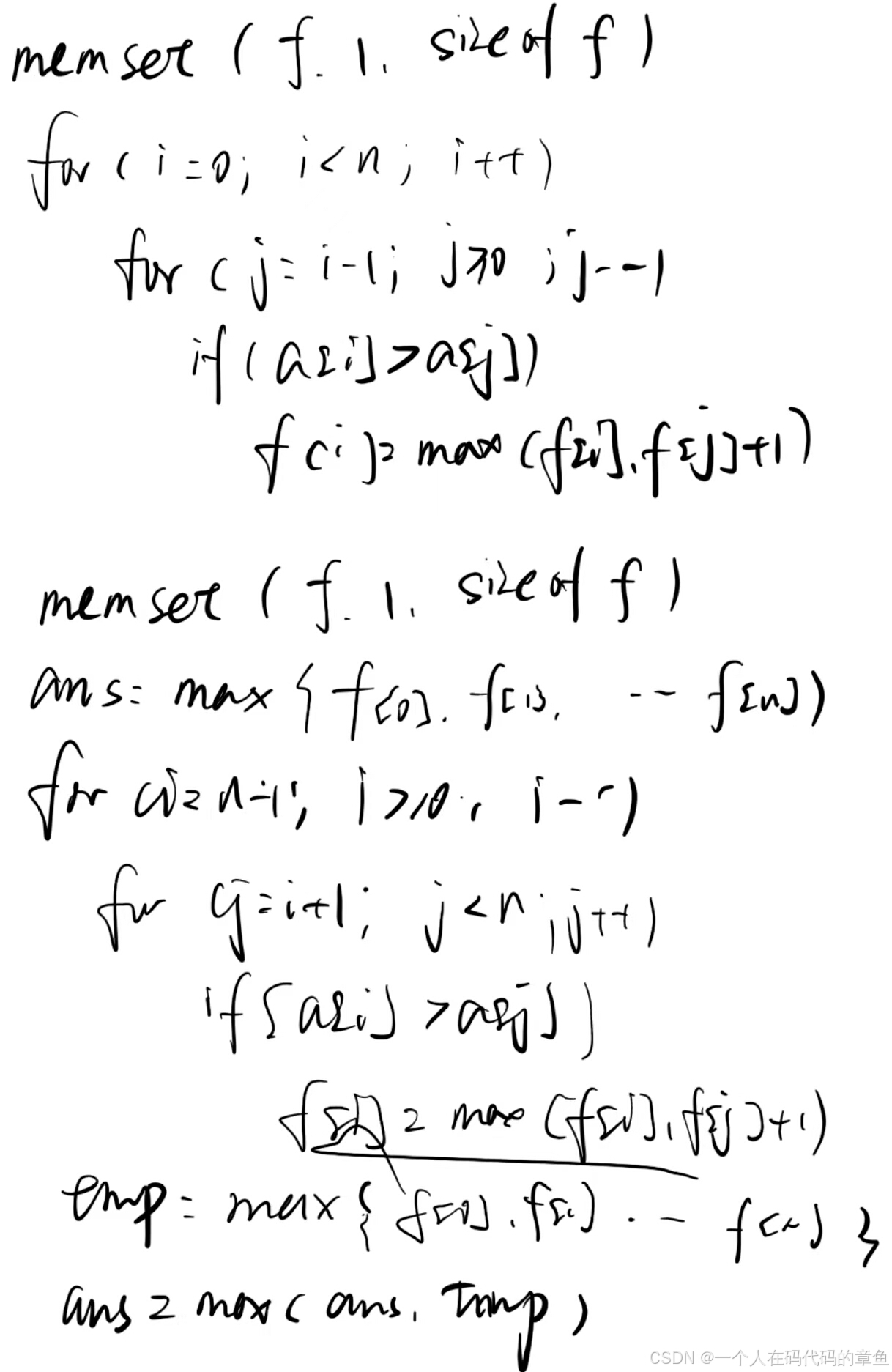



























 1142
1142

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








