2024年鸿蒙最新数据结构与算法基础-(1)(5)，2024年最新面试题题目

深知大多数程序员，想要提升技能，往往是自己摸索成长，但自己不成体系的自学效果低效又漫长，而且极易碰到天花板技术停滞不前！

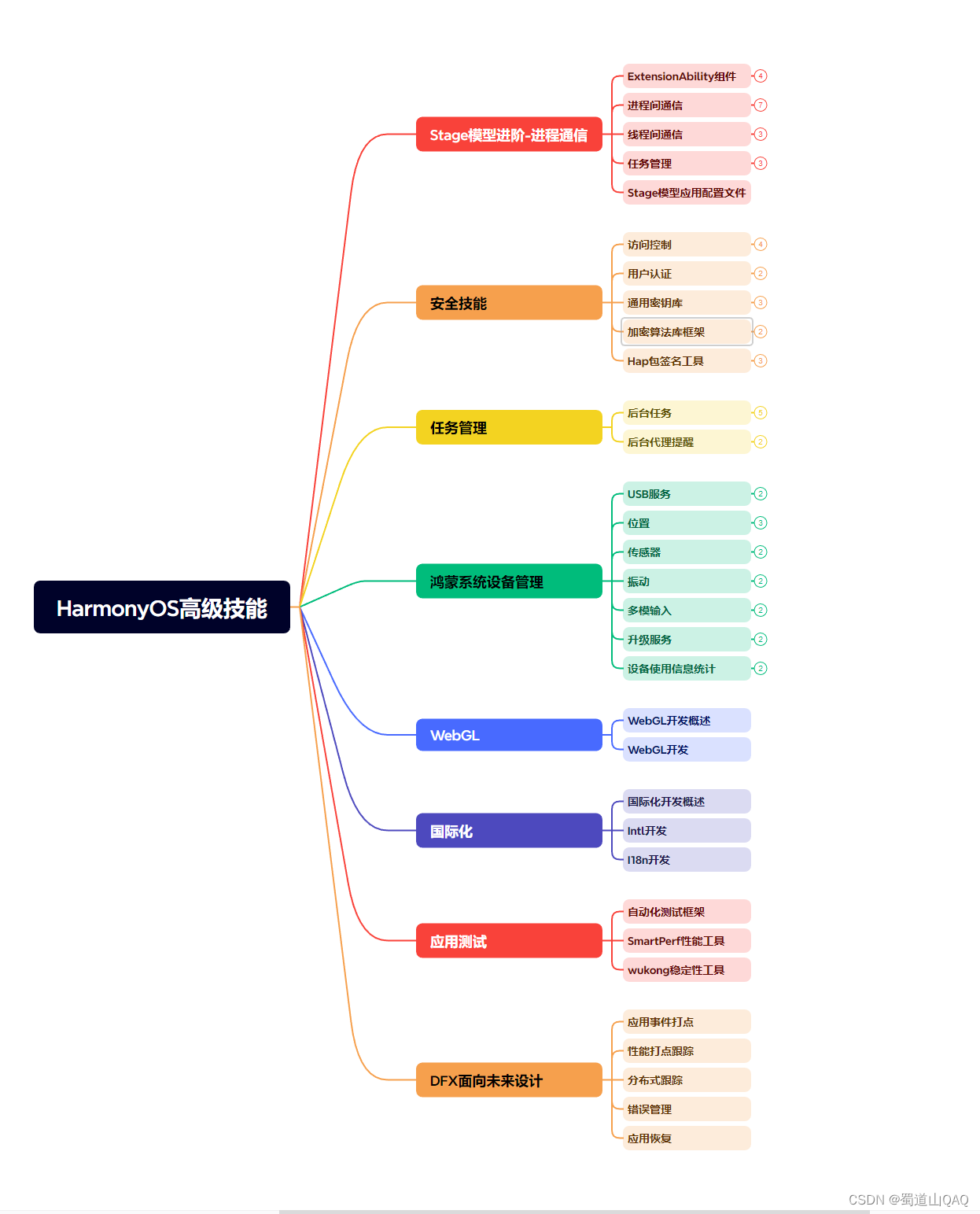
既有适合小白学习的零基础资料，也有适合3年以上经验的小伙伴深入学习提升的进阶课程，涵盖了95%以上鸿蒙开发知识点，真正体系化！

由于文件比较多，这里只是将部分目录截图出来，全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频，并且后续会持续更新

需要这份系统化的资料的朋友，可以戳这里获取

1.1数据结构与算法的概念及介绍🌱95f7939886824650b50fbc52f70adda5.png

1.2时间复杂度(Time complexity)的引入🪴

算法1:

#如果 a+b+c=1000, 且 a^2 + b^2 = c^2 (a,b,c 为自然数), 如何求出所有a,b,c 可能的组合
import time
start_time = time. time()
for a in range (0,1001):
    for b in range (0,1001):
        for c in range (0,1001):
            if a+b+c==1000 and a**2+b**2==c**2:
                print("a:",a,"b:",b,"c",c)

#获取时间
end_time = time. time()
print("所花费的时间:",(end_time - start_time))

算法2:

#如果 a+b+c=1000, 且 a^2 + b^2 = c^2 (a,b,c 为自然数), 如何求出所有a,b,c 可能的组合
import time
start_time = time. time()
for a in range (0,1001):
    for b in range (0,1001):
        c = 1000 - a - b
        if a**2+b**2==c**2:
            print("a:",a,"b:",b,"c",c)

#获取时间
end_time = time. time()
print("所花费的时间:",(end_time - start_time))

通过对比算法1和算法2 可知 单纯依靠运行的时间来比较算法的优劣并不一定是客观准确的!程序的运行离不开计算机环境(包括硬件和操作系统) ~

这些客观原因会影响程序运行的速度并反应在程序的执行时间上。

那么如何才能客观的评判一个算法的优劣呢?

---

我们引入 时间复杂度

一个算法花费的时间与算法中语句的执行次数是成正比的。哪个算法语句执行的次数多，它花费的时间就多。

如何计算一个程序的执行次数:

注:下面代码示例都是将a+b+c的和记作n,进行执行次数的计算

一段语句我们就粗略记作1次.

对于算法进行特别具体的细致分析虽然很好，但是实践中的实际价值有限。

对于算法最重要的是 数量级和趋势~~，这些是分析算法主要的部分。

对于算法最重要的是数量级和趋势，计量算法基本操作数量的规模函数中常量因子可以忽略不计。

通过比较 x^2 和 2x^2 的函数图像可知: 常量只影响陡峭程度，不影响趋势,而算法最重要的是数量级和趋势.

时间复杂度T(n)[Time complexity]:一个程序最终执行的次数来衡量算法的优劣-------eg: T(n)=2n^2
大o记法O(n)[Big O notation]:为时间复杂度的o渐进法（即忽略时间复杂度里面的常数）------eg: O(n)=n^2

深知大多数程序员，想要提升技能，往往是自己摸索成长，但自己不成体系的自学效果低效又漫长，而且极易碰到天花板技术停滞不前！

既有适合小白学习的零基础资料，也有适合3年以上经验的小伙伴深入学习提升的进阶课程，涵盖了95%以上鸿蒙开发知识点，真正体系化！

由于文件比较多，这里只是将部分目录截图出来，全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频，并且后续会持续更新

需要这份系统化的资料的朋友，可以戳这里获取

上鸿蒙开发知识点，真正体系化！**

由于文件比较多，这里只是将部分目录截图出来，全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频，并且后续会持续更新

需要这份系统化的资料的朋友，可以戳这里获取