【算法入门&amp；二叉树】从先中后序的遍历到用中后序列构造二叉树 如何抵挡递归法该死的魅力_ab16 实现二叉树先序,中序和后序遍历(2)

网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。

需要这份系统化资料的朋友，可以戳这里获取

一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！

从示例中的返回值可以看出，题目要求最终返回一个 二维数组，那么就利用灵活的 vector 容器来解题：

• 先使用递归法写好三个序列的遍历序列
• 然后用三个一维 vector容器分别存放前、中、后的遍历序列
• 最后将三个一维容器插进一个二维 vector 容器中并返回

1.2、代码实现及注释

本题源码：

/\*\*
 \* struct TreeNode {
 \* int val;
 \* struct TreeNode \*left;
 \* struct TreeNode \*right;
 \* };
 \*/

class Solution {
  public:
    /\*\*
 \*
 \* @param root TreeNode类 the root of binary tree
 \* @return int整型vector<vector<>>
 \*/
    vector<vector<int> > res; // 二维动态数组 res
    vector<int> preorder, inorder, postorder; // 存放三个序列的一维数组
    vector<vector<int> > threeOrders(TreeNode\* root) {
        preOrder(root);
        inOrder(root);
        postOrder(root);
        // 插入二维数组中
        res.push\_back(preorder);
        res.push\_back(inorder);
        res.push\_back(postorder);
        return res;
    }
    // 先序遍历
    void preOrder(TreeNode\* root) {
        if (!root) return;
        preorder.push\_back(root->val); 
        preOrder(root->left); // 访问左子树
        preOrder(root->right); // 访问右子树
    }
    // 中序遍历
    void inOrder(TreeNode\* root) {
        if (!root) return;
        inOrder(root->left); // 访问左子树
        inorder.push\_back(root->val); 
        inOrder(root->right); // 访问右子树
    }
    // 后序遍历
    void postOrder(TreeNode\* root) {
        if (!root) return;
        postOrder(root->left); // 访问左子树
        postOrder(root->right); // 访问右子树
        postorder.push\_back(root->val); 
    }
};

重要注释：

• 先、中、后序遍历的区别乍一看就是访问结点的顺序不同，但是如果去分析递归你会发现：
  • 先序遍历：访问到一个结点后，先将值插入数组，然后往左右子树递归，不为空就插入数据，为空就停止递归。
  • 中序遍历：一直往根结点的左子树递推，最先插入数据的一定是二叉树最左的一个结点，然后是根结点、右结点。
  • 后序遍历：与中序类似，区别是插入最左边结点后，先处理右子树在处理根结点。
• 先序最好理解，像是一步步的顺序进行；而中序和后序都要先递推到最左的子树然后再回溯。

2、AB17 从中序与后序遍历序列构造二叉树

利用了 无序 的哈希 map容器，解法巧妙，快来围观！

题目链接：构造二叉树

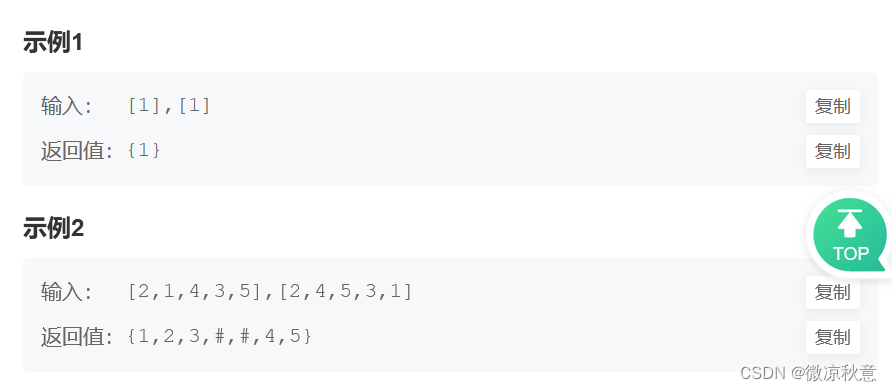
2.1、解题思路

刚看到题目不要慌，我们知道后序遍历的步骤是：左、右、根，说明后序序列的最后一个元素就是二叉树的根结点。

而中序遍历的步骤是：左、根、右，那么我们只要知道根结点在中序序列的位置就可以确定构建左右子树的范围了：最左与根结点位置之间用来构造左子树，根结点与最右用来构建右子树。

怎么确定根结点位置呢？那就要借助 unordered_map 容器：

• 这个容器底层是二叉树实现，无自动排序，可去重
• 根据中序的值来从零存放下标，这样做就可以根据值来找位置了

注意递归结束的条件：左边界大于右边界，不难想到左右边界相等时的情况是构建了边界结点。

2.2、代码实现及注释

本题源码：

/\*\*
 \* struct TreeNode {
 \* int val;
 \* struct TreeNode \*left;
 \* struct TreeNode \*right;
 \* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 \* };
 \*/
class Solution {
    int post_idx;
    unordered_map<int, int> idx_map;
public:
    /\*\*
 \* 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 \*
 \* 
 \* @param inorder int整型vector 中序遍历序列
 \* @param postorder int整型vector 后序遍历序列
 \* @return TreeNode类
 \*/
    TreeNode\* helper(int in_left,int in_right,vector<int>& inorder,vector<int>& postorder){
        if(in_left>in_right){
            return nullptr;
        }
        // 选择 post\_idx 位置的元素作为当前子树根结点
        int root_val = postorder[post_idx];
        TreeNode\* root = new TreeNode(root_val);
        // 根据 root 所在位置分成左右两棵子树
        int index = idx_map[root_val];
        // 下标减一
        post_idx--;
        // 构造右子树
        root->right=helper(index + 1, in_right, inorder, postorder);
        // 构造左子树
        root->left=helper(in_left, index - 1, inorder, postorder);
        return root;
    }
    TreeNode\* buildTree(vector<int>& inorder, vector<int>& postorder) {
        // 从后序遍历的最后一个元素开始，是先序根结点
        post_idx = (int)postorder.size()-1;


![img](https://img-blog.csdnimg.cn/img_convert/a8925fbb319c661187d09b5afb646bb7.png)
![img](https://img-blog.csdnimg.cn/img_convert/b5836bedfd5ba8e8dddea44ddef78428.png)

**网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。**

**[需要这份系统化资料的朋友，可以戳这里获取](https://bbs.youkuaiyun.com/topics/618545628)**


**一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！**

技术提升。**

**[需要这份系统化资料的朋友，可以戳这里获取](https://bbs.youkuaiyun.com/topics/618545628)**


**一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！**