基于SOM聚类算法的数据聚类可视化解析（以Python为例）

默默科研仔

于 2025-04-04 23:28:07 发布

阅读量931

点赞数 19

分类专栏：数据聚类文章标签：算法聚类 python

本文链接：https://blog.youkuaiyun.com/2401_84423592/article/details/147004453

版权

数据聚类专栏收录该内容

7 篇文章

订阅专栏

基于SOM聚类算法的数据聚类可视化解析

一、SOM算法的基本原理与特点

自组织映射（Self-Organizing Map, SOM）是一种无监督神经网络算法，通过模拟人脑神经元的自组织特性，将高维数据映射到低维（通常为2D）网格中，同时保持拓扑结构。其核心步骤包括：

初始化：随机分配神经元的权重向量，或采用Nguyen-Widrow等优化方法（如所述）。
竞争：输入数据与神经元权重计算欧几里得距离，选择距离最小的神经元作为最佳匹配单元（BMU）。
合作与适应：更新BMU及其邻域神经元的权重，使其更接近输入向量。邻域范围随迭代逐渐缩小，以平衡全局探索与局部优化。
收敛：重复上述步骤直至权重稳定或达到预设迭代次数。

特点与优势：

拓扑保持性：相似数据在网格中相邻分布，便于观察簇间关系。
可视化友好：降维后的网格可直接用于热图、U矩阵等可视化。
无需预设簇数：网格大小决定簇的细粒度，适合探索性分析。

与K-means的对比：

SOM通过邻域更新保持拓扑，而K-means仅更新质心。
当神经元数量少时，SOM与K-means效果相似；神经元增多时，SOM能揭示更复杂结构。

二、数据预处理的关键步骤

SOM对数据质量敏感，需严格预处理：

标准化：Min-Max（缩放到[0,1]）或Z-Score标准化，消除量纲差异。
缺失值处理：通过插补或删除解决数据不完整问题。
降维：对高维稀疏数据，采用PCA或LDA减少特征数量，提升聚类密度。
特征选择：剔除低相关性特征，增强数据密度。

案例：在地下水化学分析中，δ²H、δ¹⁸O等11个参数经标准化后输入SOM，成功识别同质水文组。

三、SOM聚类的实现步骤（以Python为例）

# 示例代码（基于）
from minisom import MiniSom
import numpy as np

# 数据生成与标准化
data = np.random.rand(100, 5)  # 100个样本，5维特征
data = (data - data.min(axis=0)) / (data.max(axis=0) - data.min(axis=0))  # Min-Max标准化

# 初始化SOM（5x5网格）
som = MiniSom(5, 5, 5, sigma=1.0, learning_rate=0.5)
som.random_weights_init(data)
som.train(data, 1000, verbose=True)  # 训练1000次

# 预测簇标签
winners = np.array([som.winner(x) for x in data])
clusters = np.ravel_multi_index(winners.T, (5,5))  # 将二维坐标转换为一维簇标签

四、聚类可视化的常用方法

U矩阵（Unified Distance Matrix）：
- 显示神经元间的距离，高值区域（深色）代表簇边界。
```
plt.pcolor(som.distance_map().T, cmap='bone_r')
plt.colorbar()
```
成分平面（Component Planes）：
- 每个特征单独映射到网格，观察特征分布规律。
热力图与散点图叠加：
- 用颜色区分簇，散点标记样本位置（见图7，）。
3D可视化：
- 对地理数据等复杂场景，采用RGB颜色编码三维SOM，提升聚类质量。

案例：在客户细分中，SOM热图显示年龄、收入等特征的聚集区域，结合K-means划分最终簇。

五、工具与库推荐

Python：
- MiniSOM：轻量级库，支持快速训练与可视化。
- Somoclu：支持多核CPU/GPU加速，适合大规模数据。
R：
- kohonen包：提供SOM训练、热图与聚类分析功能。
MATLAB：
- SOM Toolbox：包含批处理算法、U矩阵可视化。

六、应用场景与挑战

典型应用：

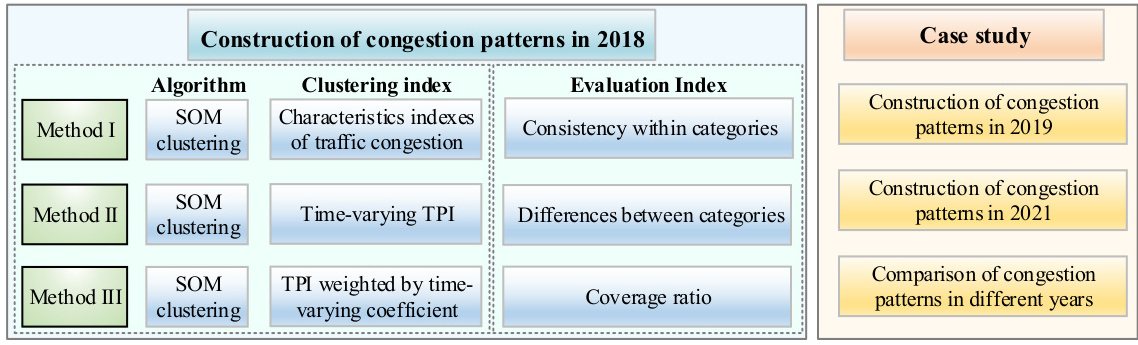
交通拥堵分析：基于时间序列TPI指数，SOM识别不同时段的拥堵模式。
基因表达聚类：将高维基因数据映射到2D网格，发现表达模式相似的样本。
图像分割：对像素特征聚类，实现图像区域划分。

挑战：

参数调优：学习率、邻域函数等需经验调整。
局部最优：初始权重敏感，需多次运行验证稳定性。
高维数据处理：需结合降维技术避免网格过度稀疏。

七、总结

SOM通过拓扑映射与竞争学习，为高维数据提供了直观的可视化手段。其核心价值在于平衡降维与结构保持，适用于探索性分析与模式发现。结合预处理、合适的可视化工具及参数优化，SOM能在客户细分、生物信息学等领域发挥重要作用。未来，随着GPU加速与交互式可视化工具的发展，SOM在处理大规模数据时的实用性将进一步提升。