基于DBSCAN聚类数据可视化的系统性解析Python代码_python dbscan聚类可视化-优快云博客

本文链接：https://blog.youkuaiyun.com/2401_84423592/article/details/147004415

基于DBSCAN聚类数据可视化的系统性解析

一、DBSCAN算法核心原理与特点

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是一种基于密度的聚类算法，其核心思想是通过邻域半径（ε）和最小样本数（min_samples）定义数据点的密度，将高密度区域连接成簇，同时识别噪声点。以下是其核心概念：

点类型：
- 核心点：在ε邻域内至少包含min_samples个点的数据点。
- 边界点：属于某个簇但自身不满足核心点条件的点。
- 噪声点：既非核心点也非边界点的离群点。
密度传播关系：
- 直接密度可达：点B在点A的ε邻域内，且A是核心点。
- 密度可达：通过一系列直接密度可达路径连接的点。
- 密度相连：存在一个核心点，使得两个点均与其密度可达。

算法特点：

优势：可发现任意形状的簇，对噪声鲁棒性强，无需预设簇数量。
局限性：对参数敏感，难以处理密度差异大的数据或嵌套簇。

二、数据预处理对DBSCAN的影响

数据预处理是提升DBSCAN聚类效果的关键步骤，主要方法包括：

标准化与归一化：
- 消除特征尺度差异，例如使用Z-score标准化。
降维处理：
- PCA：通过主成分分析减少高维数据的冗余，保留主要方差。
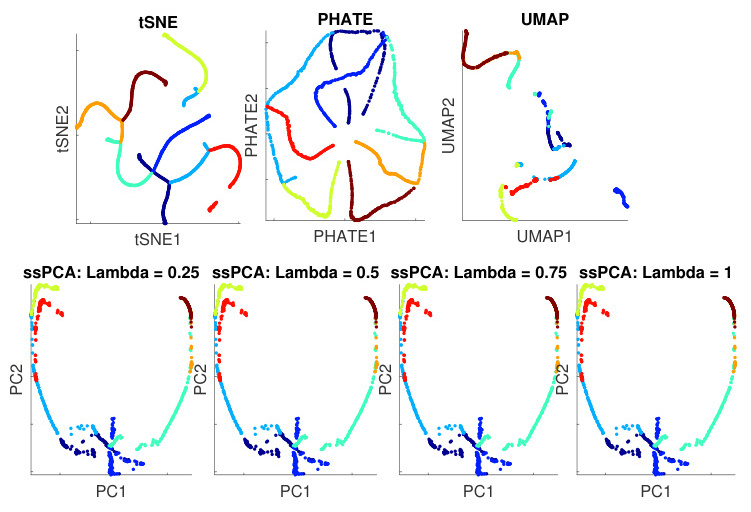
- t-SNE：非线性降维方法，适用于保持局部结构的高维数据可视化。
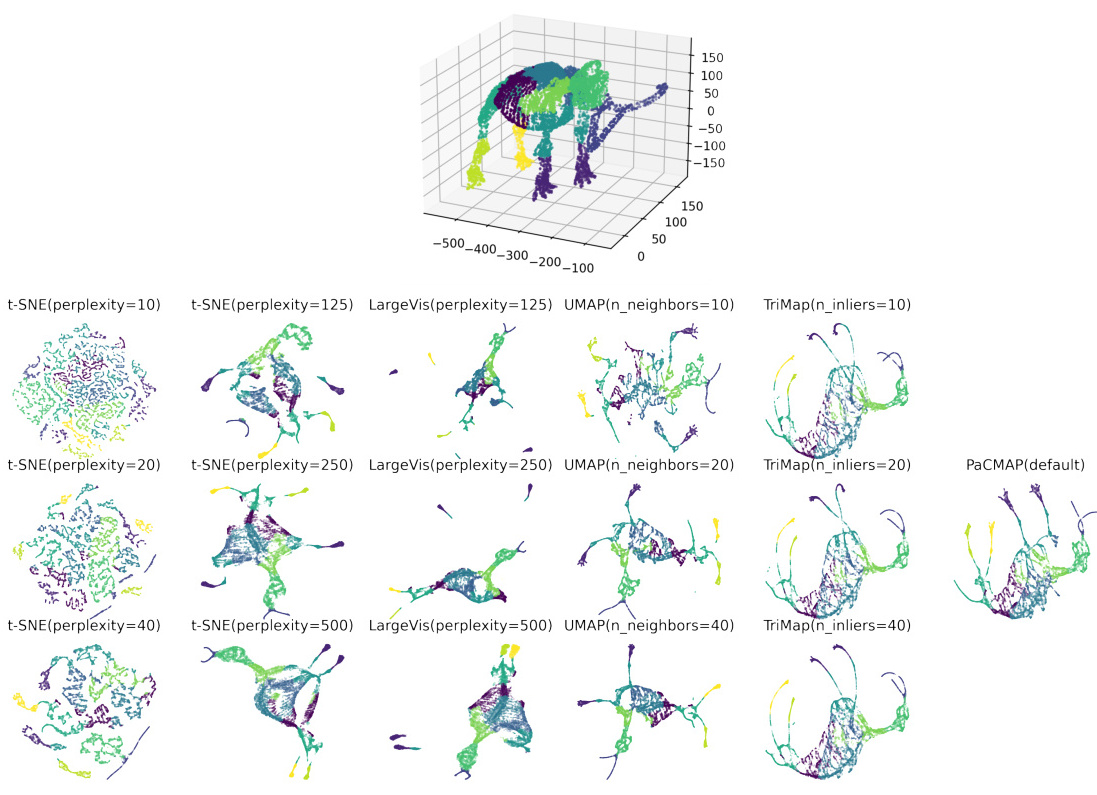
- UMAP：结合全局与局部结构，计算效率优于t-SNE。
缺失值处理与噪声过滤：
- 填充或删除缺失值，避免算法因数据不完整而失效。

案例：在Python中，通常先通过StandardScaler标准化数据，再使用PCA将数据降至2D或3D，最后应用DBSCAN聚类。

三、参数选择方法

DBSCAN的参数选择直接影响聚类结果，需结合数据集特性调整：

ε（eps）的确定：
- k-距离图法：计算每个点到其第k个最近邻的距离，绘制排序后的距离曲线，选择“肘部”对应的距离作为ε。通常k=2N-1（N为数据维度）。
- 可视化辅助：通过散点图观察数据分布，初步估计ε范围。
min_samples的选择：
- 经验规则：通常设置为数据维度的2倍（如10维数据选20）。
- 鲁棒性调整：数据噪声较多时需增大min_samples。

示例方法：使用sklearn.neighbors.NearestNeighbors计算k-距离，并通过Matplotlib绘制曲线确定ε（图1）。

四、聚类结果可视化方法

DBSCAN的可视化需结合降维技术与图表类型，具体步骤如下：

降维映射：
- 低维投影：对高维数据应用PCA或t-SNE，生成2D/3D坐标。
- 参数设置：t-SNE的perplexity需根据数据复杂度调整（通常10-30）。
图表类型：
- 散点图：最常用方法，用颜色区分不同簇和噪声点（图2）。
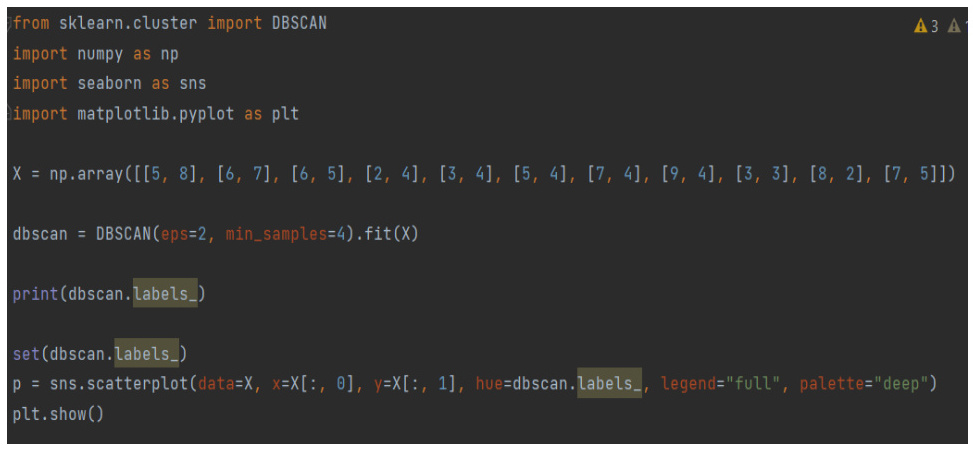
- 热力图：展示数据密度分布，辅助识别簇边界。
- 轮廓图：评估簇内紧密度与簇间分离度。
- 平行坐标图：多维数据可视化，显示各特征在簇中的分布。

Python代码示例：

from sklearn.cluster import DBSCAN
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

# 数据预处理与降维
X = PCA(n_components=2).fit_transform(data)
# DBSCAN聚类
db = DBSCAN(eps=0.3, min_samples=10).fit(X)
labels = db.labels_

# 可视化
plt.scatter(X[:,0], X[:,1], c=labels, cmap='viridis', s=20)
plt.colorbar().set_label('Cluster ID')
plt.title('DBSCAN Clustering with PCA')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.show()

五、效果评估与优化

评估指标：
- 轮廓系数（Silhouette Score） ：范围[-1,1]，值越大表示簇内紧凑、簇间分离。
- Calinski-Harabasz指数：通过簇间与簇内离散度比值衡量质量，值越大越好。
- 噪声点比例：过高可能需调整ε或min_samples。
参数调优：
- 网格搜索：遍历ε和min_samples组合，选择最优参数。
- 分层抽样：在大规模数据中，通过子集采样加速参数搜索。