网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。
需要体系化学习资料的朋友,可以加我V获取:vip204888 (备注网络安全)
一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!
C. ∀x(P(x)→∃yQ(x,y)
D. ∀x∃y(P(x)→Q(x,y))
D
前束范式就是所有的量词都在前面
- 设M={x | f1(x)=0},N={x | f2(x)=0},则方程f1(x)*f2(x)=0的解为( B )
A. M∩N
B. M∪N
C. M⊕N
C. M-N
f1(x)*f2(x)=0只有=要有一个为0 其结果就为0
显然是M和N的并集

在数学中,群表示一个拥有满足封闭性、满足结合律、有单位元、有逆元的二元运算的代数结构,包括阿贝尔群、同态和共轭类。
设G是一个群,则
- G满足消去律(左消去和右消去),即∀a,b,c∈G,若ab=ac,则b = c
- 任意一个元素的逆元的逆元是其本身,A 正确
- (ab)^-1 = b ^-1 * a ^-1, C错误
其余请看群的详细介绍
- 在整数集合Z上,下列定义的运算满足结合律的是( )
A. ab=b+1
B. ab=a-1
C. ab=ab-1
D. ab=a+b+1
D
如果满足结合律,则(a*b)*c=a*(b*c)
- 设简单图G所有的结点的度数之和为50,则G的边数为( )
A. 50
B. 25
C. 10
D. 5
B
既不含平行边也不含环的图为简单图
由握手定理:度数之和为变数的2倍,变数为25
- 设简单无向图G是一个有5个顶点的4-正则图,则G有( )条边。
A. 4
B. 5
C. 10
D. 20
C
正则图是指各顶点的度均相同的无向简单图
有题意,度数之和为5*4=20,边数=20 / 2 = 10
- 设集合A={1,2,3,4},A上的等价关系R= {<1,1>, <.3,2>,<2,3>,<4,4>} U IA (恒等关系),则对应于R的划分是( )
A. { {1},{2,3},{4} }
B. { {1,3},{2,4} }
C. { {1,3},{2},{4} }
D. { {1},{2},{3},{4} }
A
IA表示恒等关系,设A={a,b,c},则其上关系R={<a,a>,<b,b>,<c,c>},R便是恒等关系
本题中IA中应该是补齐<2,2><3,3>,2和3应该被分到了另外一块,应该选A

D
在数学中,若对某个集合的成员进行一种运算,生成的仍然是这个集合的元素,则该集合被称为在这个运算下闭合。
比较最大数,得到的结果还是在A中
比较最小数,结果还是在A中
最大公约数,1和10的最大公约数为1,L为任意数字,与其他的数求最大公约数,都可以在1,2,10,L中取得
若L为3,3和10 的最小公倍数为30,不在A中,D不是封闭的

C
先看看满射,单射和双射的定义
F的关系是一一对应的,满足单射,但f的值域中没有d,不满足满射的条件

B
割点和割边指拿掉某个点或某些边,连通分支数增加
割点集和桥指拿掉某些点或某条边,连通分支数增加

D
经过图的每一条边且仅一次并且行遍图中的每个顶点的回路(通路),称为欧拉回路(欧拉通路),存在欧拉回路的图,称为欧拉图
无向图G有欧拉回路当且仅当G是连通图且无奇度顶点
只有欧拉通路当且仅当图G恰有2个奇度顶点,这两个点为欧拉通路的端点

A
叶子结点度数只有1,显然不对
其余都是树的等价条件

A
幂集的个数为2^n

C
握手定理的推论:任何图中的度数为奇数的顶点的个数为偶数
可以排除A和D
对B选项,总共有6个点,有两个度数为5的点,而度数为5说明它与其他顶点都相连,反过来其它每个点都会与这两个点相连,度数不可能小于2,B错误

欧拉图中没有奇度顶点,排除A,C
哈密顿图中任意两个不相邻的顶点度数之和>=n-1
D中选择右边的两个度数为2的顶点,度数之和为4<6,D不存在哈密顿回路


C
共有6*3=18度
边数=度数之和 / 2 = 9

B
自反是全部顶点都有自环
反自反是全部顶点都没有自环
对称是顶点之间有边的话,全是双向边
反对称是顶点之间有边的话,全单向边

B
R2是将R1的单向边补成了双向边,应该是对称闭包

D
f(x)中x与y并不是一一对应,所以不是单射,f(x)的最大值6,并不是实数集R,不是满射

C
A,B,D中都有奇度顶点,无法构成欧拉图
二. 填空题
- 命题公式¬(p→q)的成真赋值_____,成假赋值____.
真:1 0 , 假: 0 0, 0 1, 1 1.
- 命题公式(p ∨ q)→p的成真赋值____,成假赋值____.
真:0 0, 0 1 , 1 1. 假:1 0.
- 命题公式p→(p∧q)的成真赋值____,成假赋值_____.
真:00,01,11,假:10
- 公式( ∀x)( ∀x)( P(y)→Q(x,z) ) ∧ (∃y)R(x,y)约束变元为____,自由变元为____.
x,y x,z
对左边部分 ∀x ∀y说明x,y是约束出现的,z是自由的
对右边∃y说明y是约束的,x是自由的
- 公式 ∀x(P(x) ∨ ∃yR(x) )→Q(x,z)约束变元为____,自由变元为_____.
约束: x,y
自由: x,z
- 设A = {a,b,{a,b} }, B={a,b},则B-A=____,A⊕B=_____.
B-A=Ø
A⊕B={ {a,b} }
- 设A={1,2,3},A上的关系R={<1,2>,<2,1>},则对称闭包s( R ) = ______,传递闭包t( R )= _____。
s( R ) = {<1,2>,<2,1>} //本身就是双向边,无需改动
t( R )={<1,2>,<2,1>,<1,1>,<2,2>} //<1,2><2,1>添加<1,1>,同时也可以看成<2,1>,<1,2>要添加<2,2>
- 设A={a,b,{a,b} },B= {a,b,c},则A⊕A= ______,A⊕B=______.
则A⊕A=Ø
A⊕B={{a,b},c}
- 一颗无向树的顶点数n与边数m的关系是____,6阶无向连通图至多有____颗不同的生成树。
m = n-1
6颗
- 设f(x)=x-1,g(x)=x^2,则复合函数(f g)(x)=_____,(g f)(x) =____.
统一规定为右复合
(f g)(x) = g(f(x))=(x-1)^2
(g f)(x) =f(g(x))=x^2-1

合成
R°S={<zx,z>|∃y<x,y>∈R∧∃z<y,z>∈S}
- 一颗无向树的顶点数n与边数m的关系是_____,设G是具有8个顶点的数,则G增加____条边才能把G变成完全图。
m =n-1
21条
无向完全图 边数m = (n*(n-1))/2
有向完全图 边数m = (n*(n-1))
总边数m = 8*7/2=28,树G有7条边
增加28-7=21条


三、 计算题

2.


- 一棵(无向)树有2结点的度为2,1个结点的度为3,3个结点的度为4,其余都是叶结点,问该树有几个叶结点?
在一个有限图中,各节点的度数总和是边数的2倍,而树中边数为节点数-1
设有x个叶子节点,先求出度数之和,d=2* 2 +1* 3 + 3*4+x;
d=19+x
顶点数:n = 2+1+3+x=6+x
边数: m=n-1 = 5+x
d=2m
19+x=10+2x
x=9
有9个叶节点
- 一颗无向树T有5片树叶,3个2度分支点,其余的分支点都是3度顶点,问T有几个顶点
设其余3度顶点有x个
总度数d=5* 1 + 3* 2 + 3*x =11+3x
顶点数: n=5+3+x =8+x
对与无向树,边数: m=n-1 =7+x
d=2m
11+3x = 14+2x
x=3
顶点数为11



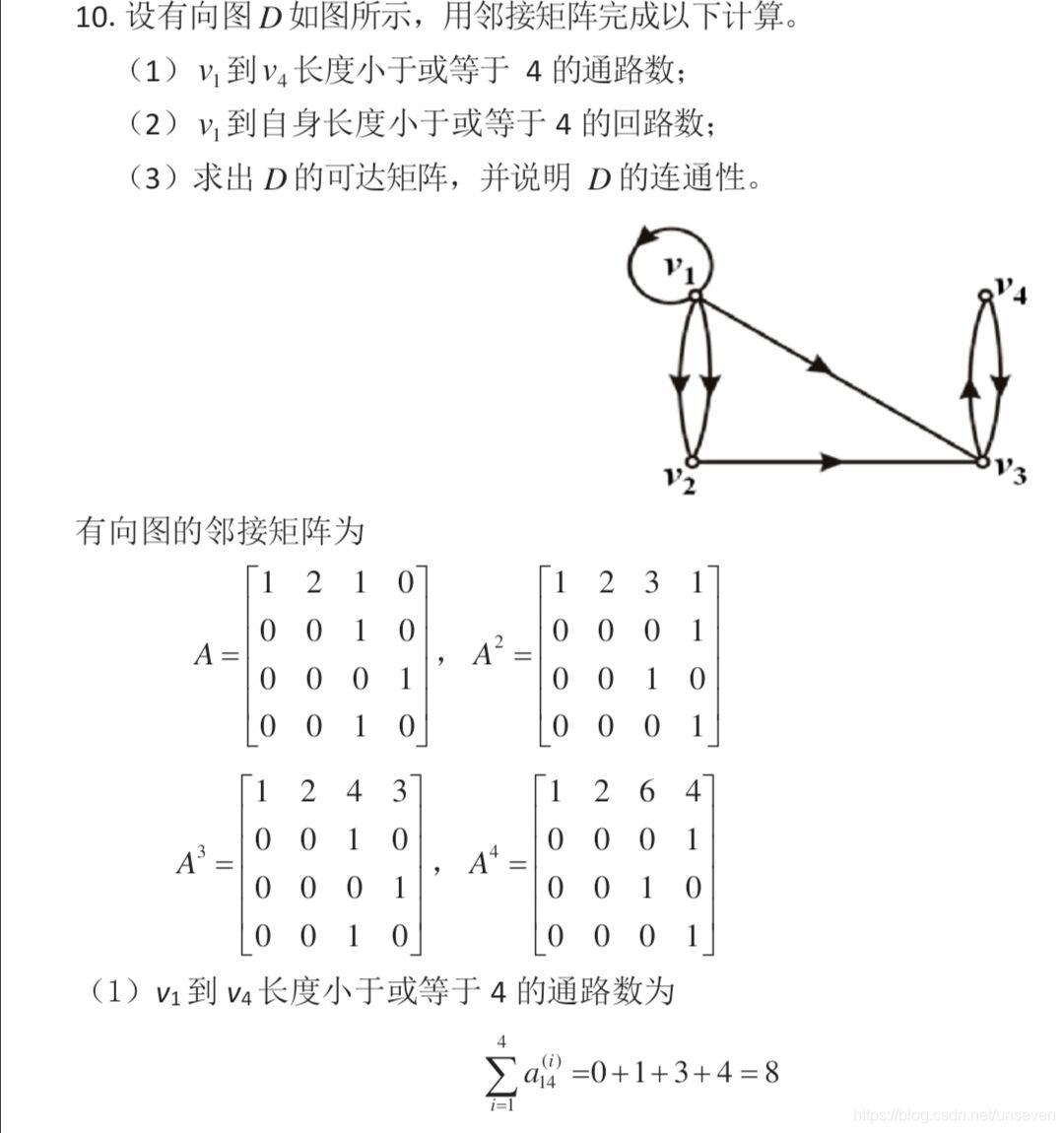


四、 简答题


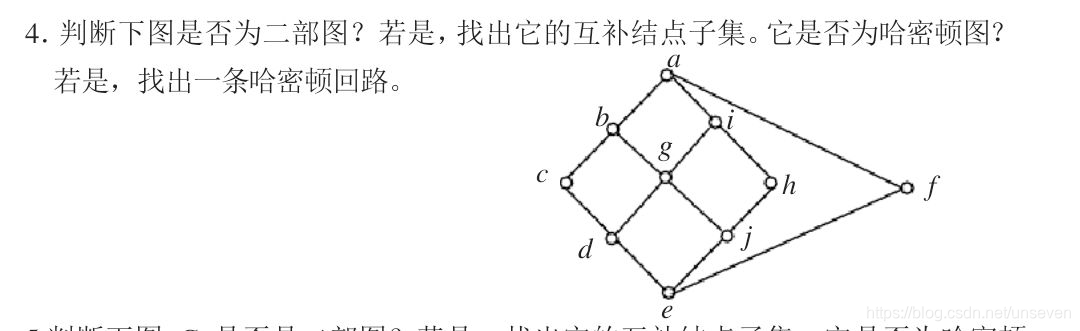
一个无向图是二部图当且仅当G中没有长度为奇数的回路
所有这个应该是一个二部图
或者看能不能化成一个二部图的样子
经过图中每个顶点一次且仅一次的回路称为哈密顿回路,有哈密顿回路的图称为哈密顿图。
如果G中任何一对不相邻的顶点的度数之和都大于等于n,则G是哈密顿图
五、 证明题
如何自学黑客&网络安全
黑客零基础入门学习路线&规划
初级黑客
1、网络安全理论知识(2天)
①了解行业相关背景,前景,确定发展方向。
②学习网络安全相关法律法规。
③网络安全运营的概念。
④等保简介、等保规定、流程和规范。(非常重要)
2、渗透测试基础(一周)
①渗透测试的流程、分类、标准
②信息收集技术:主动/被动信息搜集、Nmap工具、Google Hacking
③漏洞扫描、漏洞利用、原理,利用方法、工具(MSF)、绕过IDS和反病毒侦察
④主机攻防演练:MS17-010、MS08-067、MS10-046、MS12-20等
3、操作系统基础(一周)
①Windows系统常见功能和命令
②Kali Linux系统常见功能和命令
③操作系统安全(系统入侵排查/系统加固基础)
4、计算机网络基础(一周)
①计算机网络基础、协议和架构
②网络通信原理、OSI模型、数据转发流程
③常见协议解析(HTTP、TCP/IP、ARP等)
④网络攻击技术与网络安全防御技术
⑤Web漏洞原理与防御:主动/被动攻击、DDOS攻击、CVE漏洞复现
5、数据库基础操作(2天)
①数据库基础
②SQL语言基础
③数据库安全加固
6、Web渗透(1周)
①HTML、CSS和JavaScript简介
②OWASP Top10
③Web漏洞扫描工具
④Web渗透工具:Nmap、BurpSuite、SQLMap、其他(菜刀、漏扫等)
恭喜你,如果学到这里,你基本可以从事一份网络安全相关的工作,比如渗透测试、Web 渗透、安全服务、安全分析等岗位;如果等保模块学的好,还可以从事等保工程师。薪资区间6k-15k
到此为止,大概1个月的时间。你已经成为了一名“脚本小子”。那么你还想往下探索吗?
如果你想要入坑黑客&网络安全,笔者给大家准备了一份:282G全网最全的网络安全资料包评论区留言即可领取!
7、脚本编程(初级/中级/高级)
在网络安全领域。是否具备编程能力是“脚本小子”和真正黑客的本质区别。在实际的渗透测试过程中,面对复杂多变的网络环境,当常用工具不能满足实际需求的时候,往往需要对现有工具进行扩展,或者编写符合我们要求的工具、自动化脚本,这个时候就需要具备一定的编程能力。在分秒必争的CTF竞赛中,想要高效地使用自制的脚本工具来实现各种目的,更是需要拥有编程能力.
如果你零基础入门,笔者建议选择脚本语言Python/PHP/Go/Java中的一种,对常用库进行编程学习;搭建开发环境和选择IDE,PHP环境推荐Wamp和XAMPP, IDE强烈推荐Sublime;·Python编程学习,学习内容包含:语法、正则、文件、 网络、多线程等常用库,推荐《Python核心编程》,不要看完;·用Python编写漏洞的exp,然后写一个简单的网络爬虫;·PHP基本语法学习并书写一个简单的博客系统;熟悉MVC架构,并试着学习一个PHP框架或者Python框架 (可选);·了解Bootstrap的布局或者CSS。
8、超级黑客
这部分内容对零基础的同学来说还比较遥远,就不展开细说了,附上学习路线。

网络安全工程师企业级学习路线

如图片过大被平台压缩导致看不清的话,评论区点赞和评论区留言获取吧。我都会回复的
视频配套资料&国内外网安书籍、文档&工具
需要体系化学习资料的朋友,可以加我V获取:vip204888 (备注网络安全)
当然除了有配套的视频,同时也为大家整理了各种文档和书籍资料&工具,并且已经帮大家分好类了。

一些笔者自己买的、其他平台白嫖不到的视频教程。

网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。
一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!








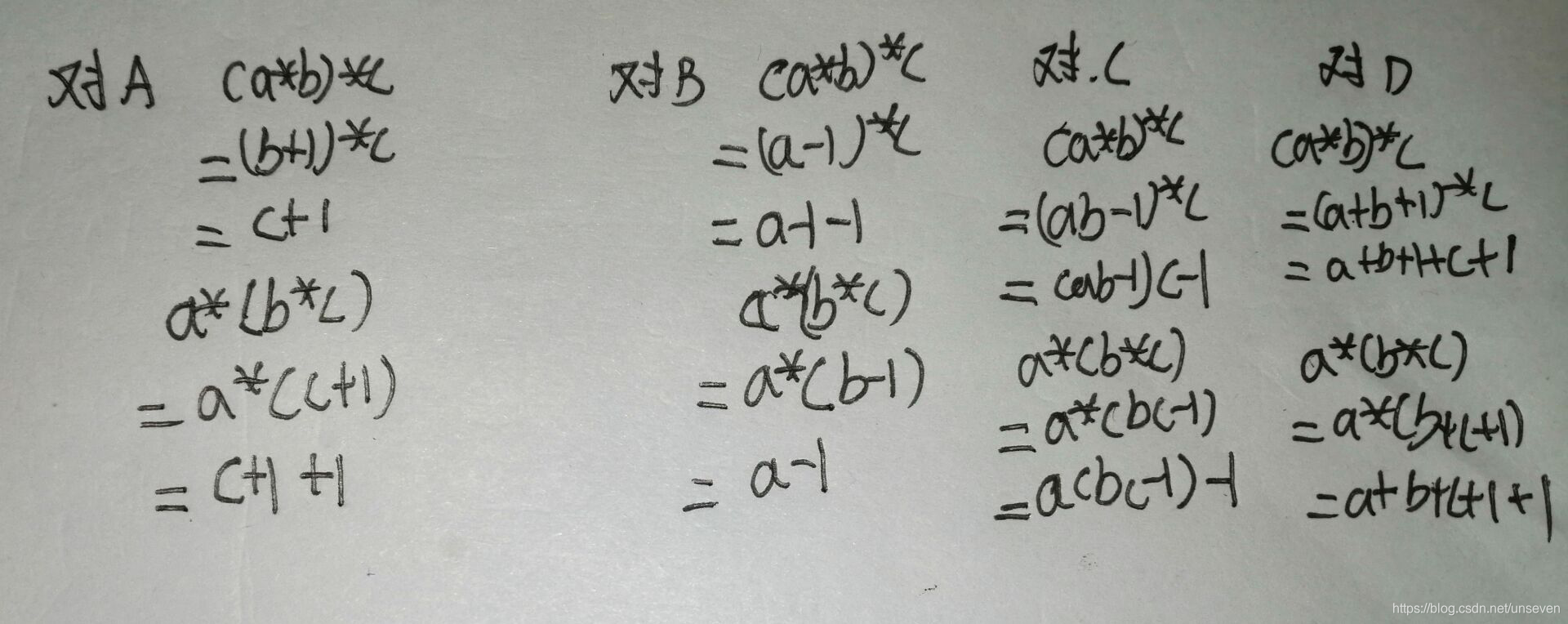



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








