超强总结！十大数据预处理技巧！！

最新推荐文章于 2025-04-08 11:34:17 发布

七七Seven～

最新推荐文章于 2025-04-08 11:34:17 发布

阅读量4.1k

点赞数 36

文章标签：人工智能 transformer pdf 学习架构

本文链接：https://blog.youkuaiyun.com/2401_84205765/article/details/142413169

版权

数据预处理确保输入数据的质量直接影响模型的性能。通过处理缺失值、标准化和特征选择，可以提高模型的准确性和稳定性。没有良好的数据预处理，即使是最复杂的模型也难以达到理想效果。

涉及到的十个数据预处理的方法：

数据清洗
数据标准化
数据编码
特征选择
特征缩放
降维
数据拆分
数据增强
数据平衡
数据转换

通过理论和案例，详细和大家聊聊~

1. 数据清洗 (Data Cleaning)

1.1 处理缺失值 (Handling Missing Values)

原理

数据缺失可能由于采集不全或错误输入等原因。在机器学习中，处理缺失值可以避免模型的偏差。

方法与公式

均值填充 (Mean Imputation)

对于缺失值，用相应特征的均值代替：

均值是数据集中值的最优估计（最小二乘估计），它使误差平方和最小化。

插值法 (Interpolation)

线性插值：假设在和之间缺失，可以通过线性插值估计：

推导：线性插值假设数据在缺失点附近变化线性，误差函数为：

通过对求导并设导数为零，得到：

解得：

1.2 处理异常值 (Handling Outliers)

原理

异常值是偏离正常数据分布的值，可能由于数据录入错误或实际存在的异常情况引起。

方法与公式

Z-Score (标准分数法)

异常值通过Z-Score判断，Z-Score定义为：

推导：

对于标准正态分布，均值为0，标准差为1。通过减去均值并除以标准差，将原数据标准化为标准正态分布。

Z-Score反映了数据点离均值的标准差数。通常，被认为是异常值，因为在正态分布中，99.7%的数据落在之间。

IQR (Interquartile Range, 四分位距)

IQR定义为数据集的第三四分位数与第一四分位数之差：

数据点小于或大于时，视为异常值。

推导：

四分位数和分别是数据排序后25%和75%处的数值。IQR捕捉了数据集中间50%的分布范围。

设定1.5倍的IQR作为界限是经验法则，用来捕捉明显的异常值。

Python案例

假设我们有一个数据集，记录了不同地区的房屋价格、面积、卧室数量以及房屋建造年份。数据集中存在一些缺失值和异常值，需要通过数据清洗进行处理。最后，我们将对数据进行标准化并展示数据分布的变化。

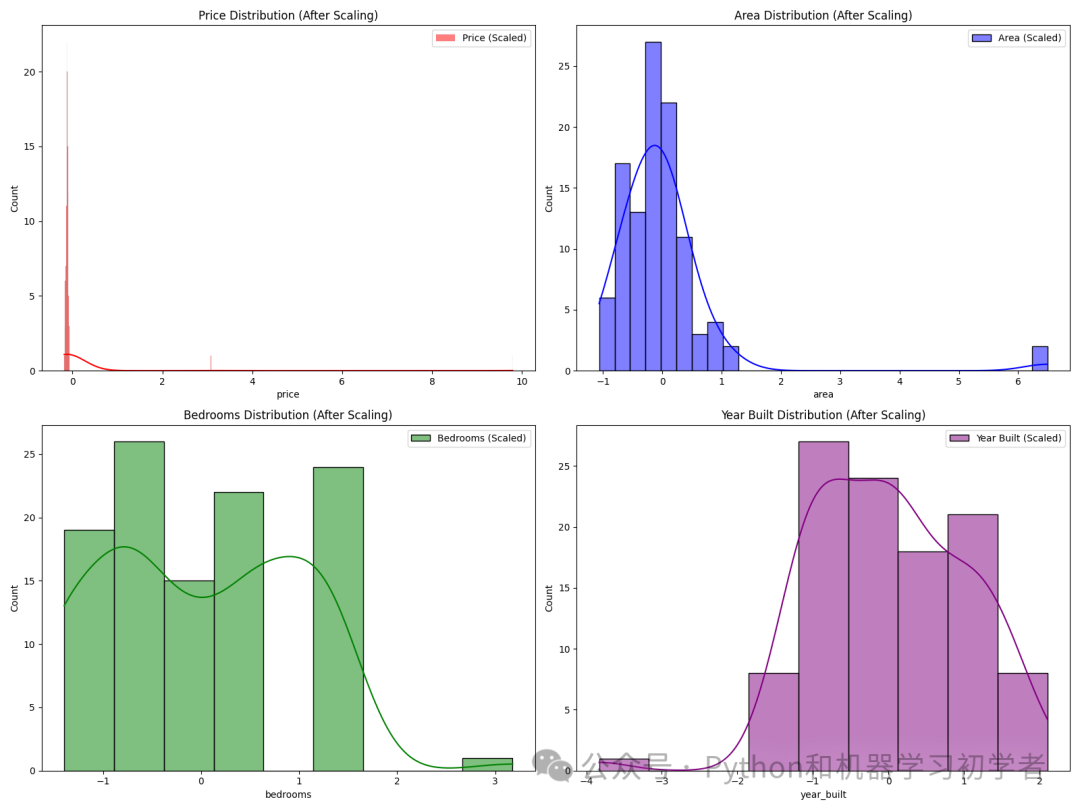
import numpy as np   import pandas as pd   import matplotlib.pyplot as plt   import seaborn as sns   from sklearn.preprocessing import StandardScaler      # 设置随机种子   np.random.seed(42)      # 生成虚拟数据集   data = {       'price': np.random.normal(300000, 75000, 100).tolist() + [np.nan]*5 + [1e7, 1e8],  # 房屋价格，包含缺失值和异常值       'area': np.random.normal(2000, 500, 100).tolist() + [np.nan]*5 + [15000, 20000],   # 房屋面积，包含缺失值和异常值       'bedrooms': np.random.randint(1, 6, 100).tolist() + [np.nan]*5 + [1, 10],          # 卧室数量，包含缺失值和异常值       'year_built': np.random.randint(1950, 2020, 100).tolist() + [np.nan]*5 + [1800, 2025]  # 建造年份，包含缺失值和异常值   }      df = pd.DataFrame(data)      # 绘制数据清洗前的分布图   plt.figure(figsize=(16, 12))      plt.subplot(2, 2, 1)   sns.histplot(df['price'], kde=True, color='red', label='Price')   plt.title('Price Distribution (Before Cleaning)')   plt.legend()      plt.subplot(2, 2, 2)   sns.histplot(df['area'], kde=True, color='blue', label='Area')   plt.title('Area Distribution (Before Cleaning)')   plt.legend()      plt.subplot(2, 2, 3)   sns.histplot(df['bedrooms'], kde=True, color='green', label='Bedrooms')   plt.title('Bedrooms Distribution (Before Cleaning)')   plt.legend()      plt.subplot(2, 2, 4)   sns.histplot(df['year_built'], kde=True, color='purple', label='Year Built')   plt.title('Year Built Distribution (Before Cleaning)')   plt.legend()      plt.tight_layout()   plt.show()      # 数据清洗步骤      # 1. 处理缺失值：使用中位数填充缺失值   df.fillna(df.median(), inplace=True)      # 2. 处理异常值：将超过三倍标准差的值视为异常值并替换为上下限   for col in df.columns:       upper_limit = df[col].mean() + 3 * df[col].std()       lower_limit = df[col].mean() - 3 * df[col].std()       df[col] = np.where(df[col] > upper_limit, upper_limit, df[col])       df[col] = np.where(df[col] < lower_limit, lower_limit, df[col])      # 3. 数据标准化   scaler = StandardScaler()   df_scaled = pd.DataFrame(scaler.fit_transform(df), columns=df.columns)      # 绘制数据清洗后的分布图   plt.figure(figsize=(16, 12))      plt.subplot(2, 2, 1)   sns.histplot(df['price'], kde=True, color='red', label='Price')   plt.title('Price Distribution (After Cleaning)')   plt.legend()      plt.subplot(2, 2, 2)   sns.histplot(df['area'], kde=True, color='blue', label='Area')   plt.title('Area Distribution (After Cleaning)')   plt.legend()      plt.subplot(2, 2, 3)   sns.histplot(df['bedrooms'], kde=True, color='green', label='Bedrooms')   plt.title('Bedrooms Distribution (After Cleaning)')   plt.legend()      plt.subplot(2, 2, 4)   sns.histplot(df['year_built'], kde=True, color='purple', label='Year Built')   plt.title('Year Built Distribution (After Cleaning)')   plt.legend()      plt.tight_layout()   plt.show()      # 绘制标准化后的数据分布图   plt.figure(figsize=(16, 12))      plt.subplot(2, 2, 1)   sns.histplot(df_scaled['price'], kde=True, color='red', label='Price (Scaled)')   plt.title('Price Distribution (After Scaling)')   plt.legend()      plt.subplot(2, 2, 2)   sns.histplot(df_scaled['area'], kde=True, color='blue', label='Area (Scaled)')   plt.title('Area Distribution (After Scaling)')   plt.legend()      plt.subplot(2, 2, 3)   sns.histplot(df_scaled['bedrooms'], kde=True, color='green', label='Bedrooms (Scaled)')   plt.title('Bedrooms Distribution (After Scaling)')   plt.legend()      plt.subplot(2, 2, 4)   sns.histplot(df_scaled['year_built'], kde=True, color='purple', label='Year Built (Scaled)')   plt.title('Year Built Distribution (After Scaling)')   plt.legend()      plt.tight_layout()   plt.show()

数据生成：我们创建了一个包含房屋价格、面积、卧室数量和建造年份的虚拟数据集。数据中故意加入了一些缺失值和异常值。
绘制原始数据的分布：使用 seaborn 绘制原始数据的分布图，以展示数据在清洗前的状态。
数据清洗：

缺失值处理：用各列的中位数填充缺失值。
异常值处理：用均值±3倍标准差范围以外的值作为异常值，并替换为上下限。

数据标准化：使用 StandardScaler 对数据进行标准化，以便将不同特征的值缩放到相同的尺度。

2. 数据标准化 (Normalization)

2.1 归一化 (Min-Max Scaling)

原理

归一化将数据缩放到指定范围（通常为[0, 1]或[-1, 1]），使得不同特征在同一量纲下进行比较，适合特征值差异较大的情况。

公式

推导

假设原始数据的最小值为，最大值为，则将数据线性缩放到 [0, 1] 范围内的目标是：

其中，缩放系数和偏移量需要满足：

解得：

代入到原公式中，得到：

2.2 标准化 (Z-Score Normalization)

原理

标准化将数据变换为均值为0、标准差为1的标准正态分布形式，用以消除不同特征之间的量纲差异。

公式

推导

假设数据的均值为，标准差为，则对数据进行标准化的目的是将其转化为标准正态分布。
原始数据的标准化过程可以看作两步：

1. 去均值：将数据的均值平移到0，即：

2. 缩放：将数据的标准差缩放到1，即：

标准化后的数据将服从标准正态分布，即均值为0，方差为1。

Python案例

假设我们有一个虚拟的数据集，包括三个不同量纲的特征：

Feature 1: 范围从 0 到 1000。
Feature 2: 范围从 0 到 50。
Feature 3: 范围从 -100 到 100。

import numpy as np   import pandas as pd   import matplotlib.pyplot as plt   from sklearn.preprocessing import MinMaxScaler      # 生成虚拟数据集   np.random.seed(42)   data = {       'Feature 1': np.random.randint(0, 1000, 100),       'Feature 2': np.random.randint(0, 50, 100),       'Feature 3': np.random.randint(-100, 100, 100)   }      df = pd.DataFrame(data)      # 数据标准化   scaler = MinMaxScaler()   df_normalized = pd.DataFrame(scaler.fit_transform(df), columns=df.columns)      # 创建绘图   fig, axes = plt.subplots(2, 3, figsize=(18, 10))      # 原始数据分布   axes[0, 0].hist(df['Feature 1'], bins=20, color='red', alpha=0.7)   axes[0, 0].set_title('Original Feature 1 Distribution')   axes[0, 1].hist(df['Feature 2'], bins=20, color='blue', alpha=0.7)   axes[0, 1].set_title('Original Feature 2 Distribution')   axes[0, 2].hist(df['Feature 3'], bins=20, color='green', alpha=0.7)   axes[0, 2].set_title('Original Feature 3 Distribution')      # 标准化后数据分布   axes[1, 0].hist(df_normalized['Feature 1'], bins=20, color='red', alpha=0.7)   axes[1, 0].set_title('Normalized Feature 1 Distribution')   axes[1, 1].hist(df_normalized['Feature 2'], bins=20, color='blue', alpha=0.7)   axes[1, 1].set_title('Normalized Feature 2 Distribution')   axes[1, 2].hist(df_normalized['Feature 3'], bins=20, color='green', alpha=0.7)   axes[1, 2].set_title('Normalized Feature 3 Distribution')      # 调整布局   plt.tight_layout()   plt.show()

数据生成: 使用 numpy 生成三个不同范围的随机数据，模拟真实世界中具有不同尺度的特征。
数据标准化: 使用 MinMaxScaler 将数据缩放到 [0, 1] 的范围内，这是一种常见的标准化方法。

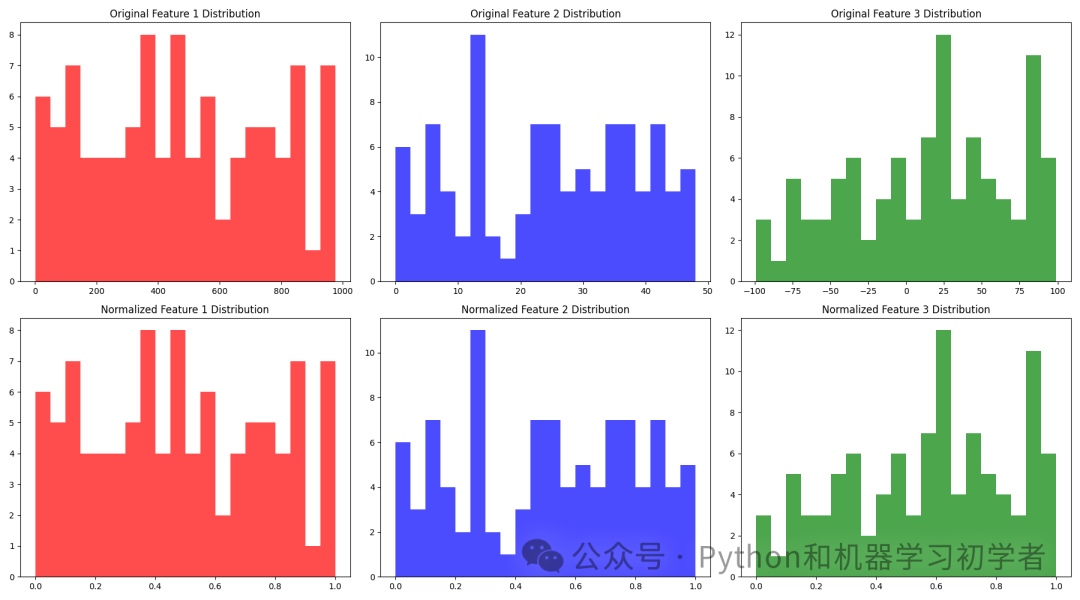
图形绘制: 使用 matplotlib 生成 6 个子图。第一行显示原始数据的分布，第二行显示标准化后数据的分布。通过对比两行的图形，可以直观地看到标准化对数据分布的影响。

3. 数据编码 (Encoding)

3.1 类别编码 (Label Encoding)

原理

类别编码将分类特征转换为整数值，适用于有序类别。

公式

假设类别变量，将其编码为：

推导

类别编码的思想是将类别标签映射为整数，通常直接根据类别的出现顺序进行编码。
对于有序类别，例如评级（低、中、高），类别编码能保留顺序信息。

3.2 独热编码 (One-Hot Encoding)

原理

独热编码将分类变量转换为二进制向量，适用于无序类别，避免了类别编码带来的顺序问题。

公式

对于类别，独热编码如下：

推导

独热编码通过构造与类别数量相同的二进制位来表示每个类别。假设有个类别，每个类别用一个长度为的二进制向量表示，且每个向量中只有一个位置为1，其余位置为0。
这种编码方式能够消除类别之间的潜在顺序关系，同时将类别转换为可用于机器学习算法（如线性模型）的特征。

Python案例

这个示例使用One-Hot Encoding和Label Encoding两种编码方法，通过图形展示了编码前后的数据分布。

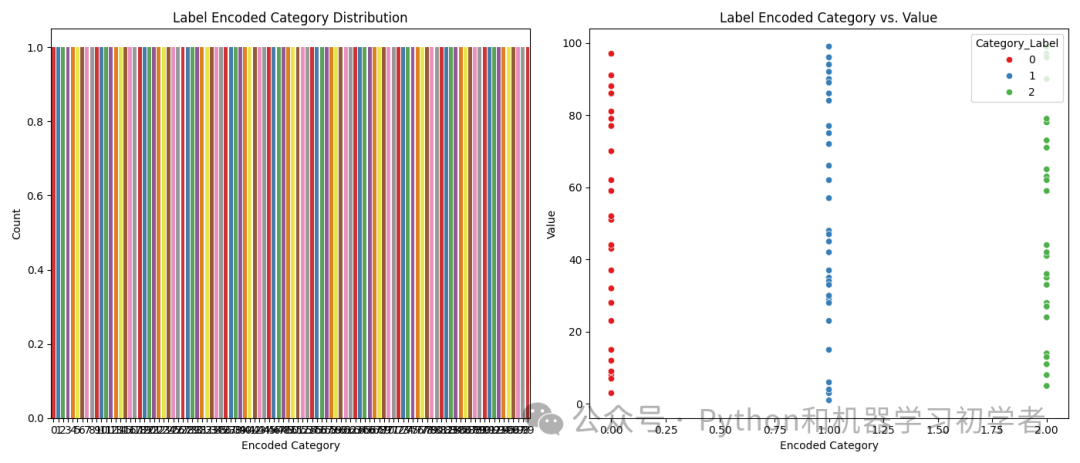
import numpy as np   import pandas as pd   import matplotlib.pyplot as plt   import seaborn as sns   from sklearn.preprocessing import LabelEncoder, OneHotEncoder      # 生成虚拟数据集   np.random.seed(42)   data = pd.DataFrame({       'Category': np.random.choice(['A', 'B', 'C'], 100),       'Value': np.random.randint(1, 100, 100)   })      # 原始数据分布图   plt.figure(figsize=(14, 6))      plt.subplot(1, 3, 1)   sns.countplot(data['Category'], palette="Set2")   plt.title('Original Category Distribution')   plt.xlabel('Category')   plt.ylabel('Count')      plt.subplot(1, 3, 2)   sns.scatterplot(x='Category', y='Value', data=data, palette="Set2", hue='Category')   plt.title('Original Category vs. Value')   plt.xlabel('Category')   plt.ylabel('Value')      # One-Hot Encoding   onehot_encoder = OneHotEncoder(sparse=False)   onehot_encoded = onehot_encoder.fit_transform(data[['Category']])   onehot_encoded_df = pd.DataFrame(onehot_encoded, columns=onehot_encoder.get_feature_names_out(['Category']))      # 将One-Hot编码后的特征加入原始数据集中   data_onehot = pd.concat([data.drop('Category', axis=1), onehot_encoded_df], axis=1)      plt.subplot(1, 3, 3)   sns.heatmap(data_onehot.corr(), annot=True, cmap="Spectral")   plt.title('Correlation Heatmap After One-Hot Encoding')      plt.tight_layout()   plt.show()      # Label Encoding   label_encoder = LabelEncoder()   data['Category_Label'] = label_encoder.fit_transform(data['Category'])      # 生成新的图表   plt.figure(figsize=(14, 6))      plt.subplot(1, 2, 1)   sns.countplot(data['Category_Label'], palette="Set1")   plt.title('Label Encoded Category Distribution')   plt.xlabel('Encoded Category')   plt.ylabel('Count')      plt.subplot(1, 2, 2)   sns.scatterplot(x='Category_Label', y='Value', data=data, hue='Category_Label', palette="Set1")   plt.title('Label Encoded Category vs. Value')   plt.xlabel('Encoded Category')   plt.ylabel('Value')      plt.tight_layout()   plt.show()

虚拟数据集生成：Category列包含三个类别’A’、‘B’和’C’。Value列包含从1到100之间的随机整数。
One-Hot Encoding：使用OneHotEncoder对Category列进行One-Hot编码。将编码后的结果添加到原始数据集，并绘制相关性热图。
Label Encoding：使用LabelEncoder将类别标签转换为数字编码。生成新的类别分布和散点图。

第一组图显示了编码前和One-Hot编码后的数据特征。
第二组图展示了使用Label Encoding编码后的数据分布。

4. 特征选择 (Feature Selection)

4.1 过滤法 (Filter Method)

原理

过滤法根据特征与目标变量之间的统计关系（如相关系数、卡方检验）来选择特征，通常用于数据预处理阶段。

方法与公式

相关系数：用于衡量连续特征与目标变量之间的线性关系。皮尔逊相关系数公式如下：

推导

皮尔逊相关系数衡量两个变量和之间的线性相关程度。
公式的分子部分是两个变量与各自均值差值的乘积之和，分母部分是这两个差值的标准差的乘积。
通过标准化和，皮尔逊相关系数将位于之间。值越接近1或-1，表示线性关系越强。

4.2 包裹法 (Wrapper Method)

原理

包裹法通过训练模型并使用模型性能来选择特征子集。常见方法有递归特征消除（RFE）。

步骤与公式

递归特征消除 (RFE)

使用初始特征集训练模型，计算每个特征的重要性。
移除最不重要的特征，重新训练模型。
重复上述过程，直到选定的特征数目达到预设的目标。

推导

递归特征消除的思想是逐步移除对模型贡献最小的特征。通过反复训练和特征移除，最终选择最优的特征子集。
这种方法计算量较大，因为需要多次训练模型，但通常能够获得比简单过滤法更好的结果。

4.3 嵌入法 (Embedded Method)

原理

嵌入法在模型训练过程中自动选择重要特征，常见方法如Lasso回归。

公式

Lasso回归：Lasso通过加入正则化项来进行特征选择：

推导

Lasso回归的目标是通过惩罚模型的复杂度（即权重的绝对值和）来选择重要特征。
正则化项使得一些特征的权重被压缩为零，从而实现特征选择。
Lasso的这一特性来自于范数的凸性和稀疏性。相比于范数（如Ridge回归），范数更倾向于产生稀疏解，即大部分权重为零的解。

Python案例

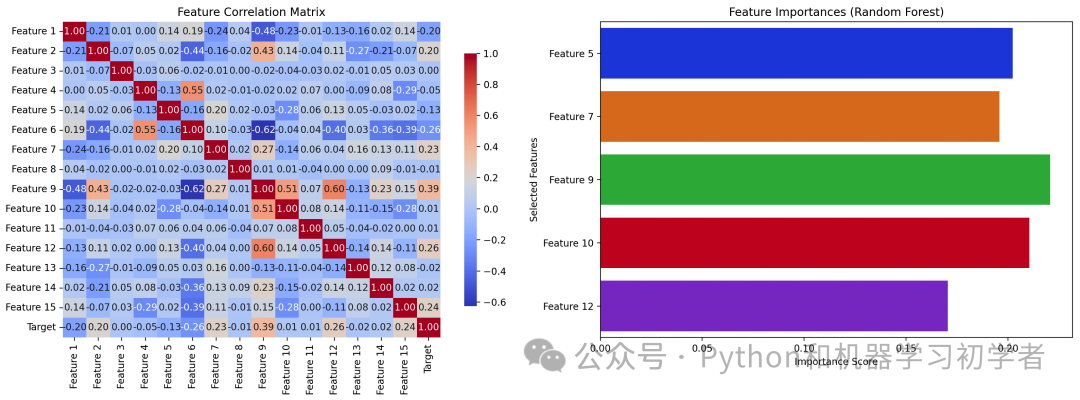
应用特征选择技术来选择最相关的特征，并通过绘制相关性热图和特征重要性图来可视化数据分析的结果。

import numpy as np   import pandas as pd   import matplotlib.pyplot as plt   import seaborn as sns   from sklearn.ensemble import RandomForestClassifier   from sklearn.datasets import make_classification   from sklearn.feature_selection import SelectKBest, f_classif      # 设置随机种子   np.random.seed(42)      # 生成虚拟数据集   X, y = make_classification(n_samples=500, n_features=15, n_informative=10, n_redundant=2, n_classes=3, random_state=42)   feature_names = [f'Feature {i+1}' for i in range(X.shape[1])]   df = pd.DataFrame(X, columns=feature_names)   df['Target'] = y      # 计算相关性矩阵   correlation_matrix = df.corr()      # 选择与目标变量最相关的前5个特征   selector = SelectKBest(score_func=f_classif, k=5)   selector.fit(df[feature_names], y)   selected_features = selector.get_support(indices=True)   selected_feature_names = [feature_names[i] for i in selected_features]      # 使用随机森林计算特征重要性   model = RandomForestClassifier(random_state=42)   model.fit(df[selected_feature_names], y)   importances = model.feature_importances_      # 创建子图   fig, axs = plt.subplots(1, 2, figsize=(16, 6))      # 绘制相关性热图   sns.heatmap(correlation_matrix, annot=True, fmt='.2f', cmap='coolwarm', ax=axs[0], cbar_kws={'shrink': .8})   axs[0].set_title('Feature Correlation Matrix')      # 绘制特征重要性图   sns.barplot(x=importances, y=selected_feature_names, palette='bright', ax=axs[1])   axs[1].set_title('Feature Importances (Random Forest)')   axs[1].set_xlabel('Importance Score')   axs[1].set_ylabel('Selected Features')      # 显示图形   plt.tight_layout()   plt.show()

生成虚拟数据集: 我们使用 make_classification 生成了一个包含500个样本和15个特征的虚拟分类数据集，其中10个特征是信息性的（有助于分类），2个是冗余的，剩下的3个是无关的噪声。
相关性矩阵: 计算了特征之间的相关性，并绘制了热图，以显示特征之间的线性关系。
特征选择: 使用 SelectKBest 方法选择了与目标变量最相关的前5个特征。
特征重要性: 通过训练随机森林分类器，计算出选定特征的重要性分数，并绘制特征重要性条形图。

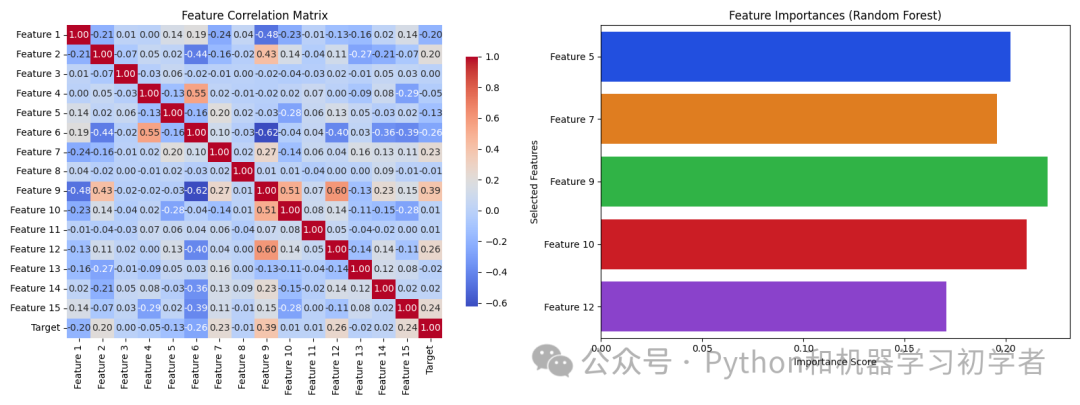
左侧图显示了所有特征的相关性矩阵，以热图的形式展现。
右侧图展示了随机森林模型计算出的前5个选定特征的重要性分数。

5. 特征缩放 (Feature Scaling)

5.1 标准化与归一化

标准化 与 归一化 在前面已经详细讨论。

5.2 对数变换 (Log Transformation)

原理

对数变换适用于数据分布右偏的特征，通过取对数，可以减小数据的量级差异，降低极端值的影响。

公式

推导

对数变换是非线性变换的一种，将数据的乘法关系转化为加法关系。
当数据集中存在较大差异时，直接处理可能不利于模型的学习。通过对数变换，可以将数据的尺度压缩，从而减少大值对模型的影响。
加1是为了防止数据中存在零值时取对数出现数学错误。

Python案例

下面是使用虚拟数据集进行特征缩放的代码示例，包括两种不同的特征缩放方法：**标准化 (Standardization)**和 最小最大缩放 (Min-Max Scaling)。

import numpy as np   import matplotlib.pyplot as plt   from sklearn.preprocessing import StandardScaler, MinMaxScaler      # 生成虚拟数据集   np.random.seed(42)   data = np.random.rand(100, 2) * 100  # 100个样本，2个特征，范围0-100之间      # 创建标准化（Standardization）和最小最大缩放（Min-Max Scaling）对象   scaler_standard = StandardScaler()   scaler_minmax = MinMaxScaler()      # 进行特征缩放   data_standardized = scaler_standard.fit_transform(data)   data_minmax_scaled = scaler_minmax.fit_transform(data)      # 绘图   fig, axs = plt.subplots(2, 2, figsize=(12, 10))      # 原始数据分布   axs[0, 0].scatter(data[:, 0], data[:, 1], color='blue', edgecolor='k', s=50, alpha=0.7)   axs[0, 0].set_title("Original Data", fontsize=14)   axs[0, 0].set_xlabel("Feature 1")   axs[0, 0].set_ylabel("Feature 2")      # 标准化后的数据分布   axs[0, 1].scatter(data_standardized[:, 0], data_standardized[:, 1], color='green', edgecolor='k', s=50, alpha=0.7)   axs[0, 1].set_title("Standardized Data", fontsize=14)   axs[0, 1].set_xlabel("Feature 1 (Standardized)")   axs[0, 1].set_ylabel("Feature 2 (Standardized)")      # 最小最大缩放后的数据分布   axs[1, 0].scatter(data_minmax_scaled[:, 0], data_minmax_scaled[:, 1], color='red', edgecolor='k', s=50, alpha=0.7)   axs[1, 0].set_title("Min-Max Scaled Data", fontsize=14)   axs[1, 0].set_xlabel("Feature 1 (Min-Max Scaled)")   axs[1, 0].set_ylabel("Feature 2 (Min-Max Scaled)")      # 原始数据与缩放后数据对比   axs[1, 1].scatter(data[:, 0], data[:, 1], color='blue', label='Original', edgecolor='k', s=50, alpha=0.5)   axs[1, 1].scatter(data_standardized[:, 0], data_standardized[:, 1], color='green', label='Standardized', edgecolor='k', s=50, alpha=0.5)   axs[1, 1].scatter(data_minmax_scaled[:, 0], data_minmax_scaled[:, 1], color='red', label='Min-Max Scaled', edgecolor='k', s=50, alpha=0.5)   axs[1, 1].set_title("Comparison of All Data", fontsize=14)   axs[1, 1].set_xlabel("Feature 1")   axs[1, 1].set_ylabel("Feature 2")   axs[1, 1].legend(loc='upper right')      # 调整图像布局   plt.tight_layout()   plt.show()

数据生成：使用 np.random.rand 生成随机数据，数据范围在0-100之间，包含100个样本，每个样本有2个特征。
特征缩放：使用 StandardScaler 和 MinMaxScaler 进行标准化和最小最大缩放。

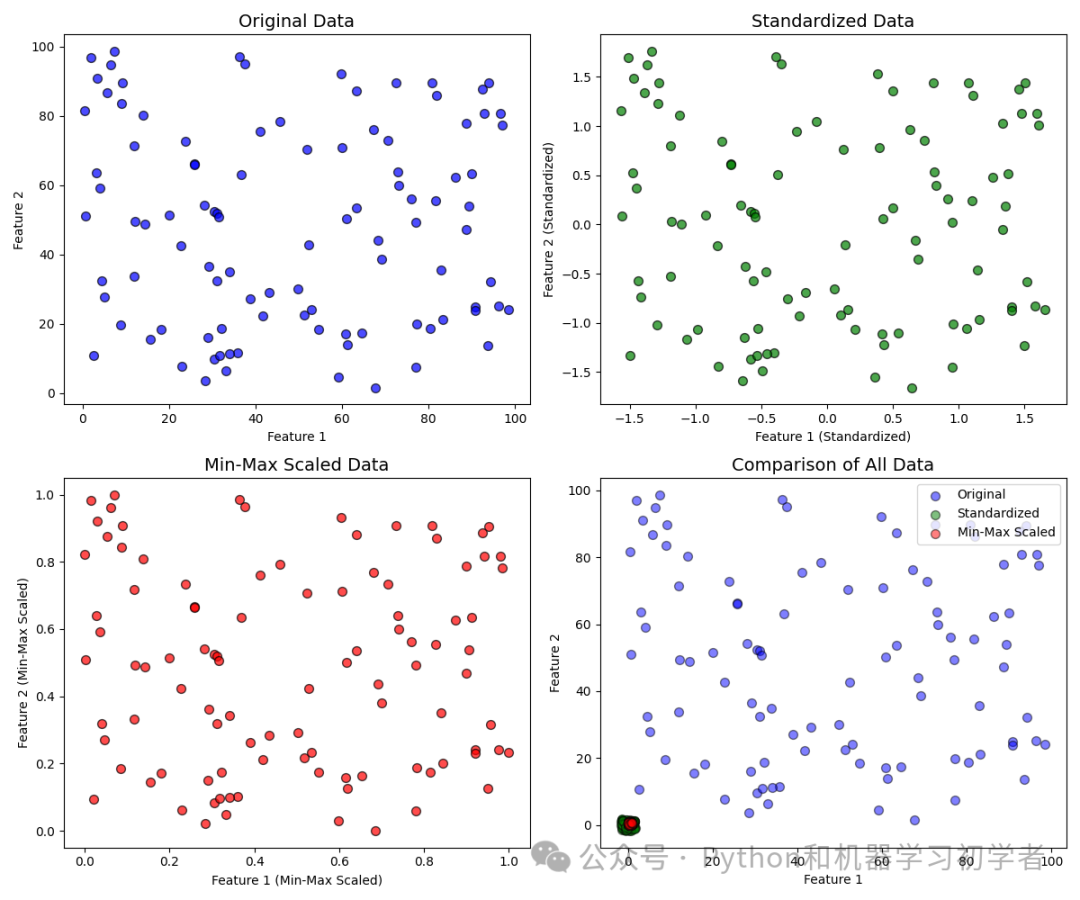
原始数据的分布图。
标准化后的数据分布图。
最小最大缩放后的数据分布图。
原始数据、标准化数据和最小最大缩放数据的对比图。

6. 降维 (Dimensionality Reduction)

6.1 主成分分析 (PCA)

原理

PCA是一种线性降维方法，通过主成分变换，将数据从高维空间投影到低维空间，保留尽可能多的方差信息。

核心公式

其中，是中心化后的数据矩阵，是主成分的权重矩阵（即特征向量矩阵），是降维后的数据。

推导

1. 数据中心化：将数据矩阵的每个特征减去均值，使得每列均值为0。

2. 计算协方差矩阵：

3. 求解特征值和特征向量：对协方差矩阵求解特征值和特征向量。

4. 选择主成分：选择对应最大特征值的前个特征向量作为主成分，形成权重矩阵。

5. 投影数据：将原始数据投影到新空间：

Python案例

下面是一个使用PCA（主成分分析）和t-SNE（t-分布随机邻域嵌入）进行降维的案例。

import numpy as np   import matplotlib.pyplot as plt   import seaborn as sns   from sklearn.datasets import make_classification   from sklearn.decomposition import PCA   from sklearn.manifold import TSNE   from sklearn.preprocessing import StandardScaler      # 生成虚拟数据集   n_samples = 1000   n_features = 20   n_classes = 4   X, y = make_classification(n_samples=n_samples, n_features=n_features,                               n_classes=n_classes, random_state=42, n_clusters_per_class=1)      # 标准化数据   scaler = StandardScaler()   X_scaled = scaler.fit_transform(X)      # PCA降维   pca = PCA(n_components=2)   X_pca = pca.fit_transform(X_scaled)      # t-SNE降维   tsne = TSNE(n_components=2, random_state=42)   X_tsne = tsne.fit_transform(X_scaled)      # 绘图   plt.figure(figsize=(12, 6))      # PCA图   plt.subplot(1, 2, 1)   sns.scatterplot(x=X_pca[:, 0], y=X_pca[:, 1], hue=y, palette='tab10', s=60, edgecolor='k')   plt.title('PCA Dimensionality Reduction')   plt.xlabel('Principal Component 1')   plt.ylabel('Principal Component 2')   plt.legend(title='Classes')      # t-SNE图   plt.subplot(1, 2, 2)   sns.scatterplot(x=X_tsne[:, 0], y=X_tsne[:, 1], hue=y, palette='tab10', s=60, edgecolor='k')   plt.title('t-SNE Dimensionality Reduction')   plt.xlabel('t-SNE Component 1')   plt.ylabel('t-SNE Component 2')   plt.legend(title='Classes')      plt.tight_layout()   plt.show()

数据生成: 使用make_classification生成一个虚拟数据集，有20个特征和4个分类。
数据标准化: 使用StandardScaler对数据进行标准化，以确保每个特征的均值为0，方差为1。
PCA降维: 将数据降维到2维，以便进行可视化。
t-SNE降维: 将数据降维到2维，用于对比PCA的效果。

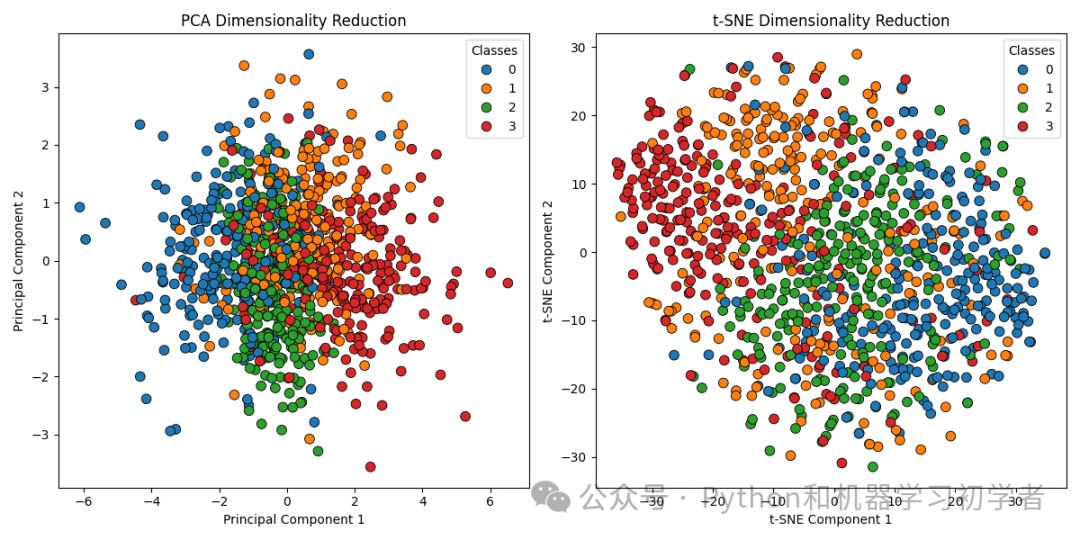
7. 数据拆分 (Data Splitting)

7.1 训练集/验证集/测试集划分

原理

将数据集划分为训练集、验证集和测试集，分别用于模型训练、参数调优和性能评估。

公式

数据划分比例通常为70:15:15或80:10:10。

7.2 交叉验证 (Cross-Validation)

原理

交叉验证通过多次划分数据集和重复训练模型，降低模型对特定数据集划分的依赖性。

方法

k折交叉验证：将数据集随机划分为k个子集，每次选择其中一个子集作为验证集，剩下的作为训练集，重复k次。

推导

通过将每个样本都作为一次验证集中的样本，使得所有数据点均参与模型的训练和验证，最终的模型性能是k次实验结果的平均值。

Python案例

import numpy as np   import matplotlib.pyplot as plt   from sklearn.model_selection import train_test_split   from sklearn.linear_model import LinearRegression      # 生成虚拟数据集   np.random.seed(42)   X = 2 * np.random.rand(100, 1)   y = 4 + 3 * X + np.random.randn(100, 1)      # 数据拆分：80% 训练集，20% 测试集   X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)      # 拟合线性回归模型   lin_reg = LinearRegression()   lin_reg.fit(X_train, y_train)      # 在训练集和测试集上做预测   y_train_pred = lin_reg.predict(X_train)   y_test_pred = lin_reg.predict(X_test)      # 设置图形大小和颜色   plt.figure(figsize=(10, 6))      # 图1：训练集与测试集数据的散点图   plt.subplot(1, 2, 1)   plt.scatter(X_train, y_train, color='blue', label='Training Data', s=50)   plt.scatter(X_test, y_test, color='red', label='Testing Data', s=50)   plt.plot(X_train, y_train_pred, color='green', label='Regression Line', linewidth=2)   plt.title('Training and Testing Data with Regression Line', fontsize=12)   plt.xlabel('X')   plt.ylabel('y')   plt.legend()      # 图2：测试集的预测结果与实际值对比   plt.subplot(1, 2, 2)   plt.scatter(X_test, y_test, color='red', label='Actual Testing Data', s=50)   plt.scatter(X_test, y_test_pred, color='orange', label='Predicted Testing Data', s=50, marker='x')   plt.plot(X_train, y_train_pred, color='green', label='Regression Line', linewidth=2)   plt.title('Testing Data: Actual vs Predicted', fontsize=12)   plt.xlabel('X')   plt.ylabel('y')   plt.legend()      # 显示图形   plt.tight_layout()   plt.show()

数据生成：创建了一个具有线性关系的虚拟数据集 y = 4 + 3X + {noise} ，其中 noise 是一些随机噪声。
数据拆分：使用 train_test_split 将数据集按 80% 和 20% 分别划分为训练集和测试集。
线性回归拟合：对训练集数据进行线性回归拟合，获取回归模型。

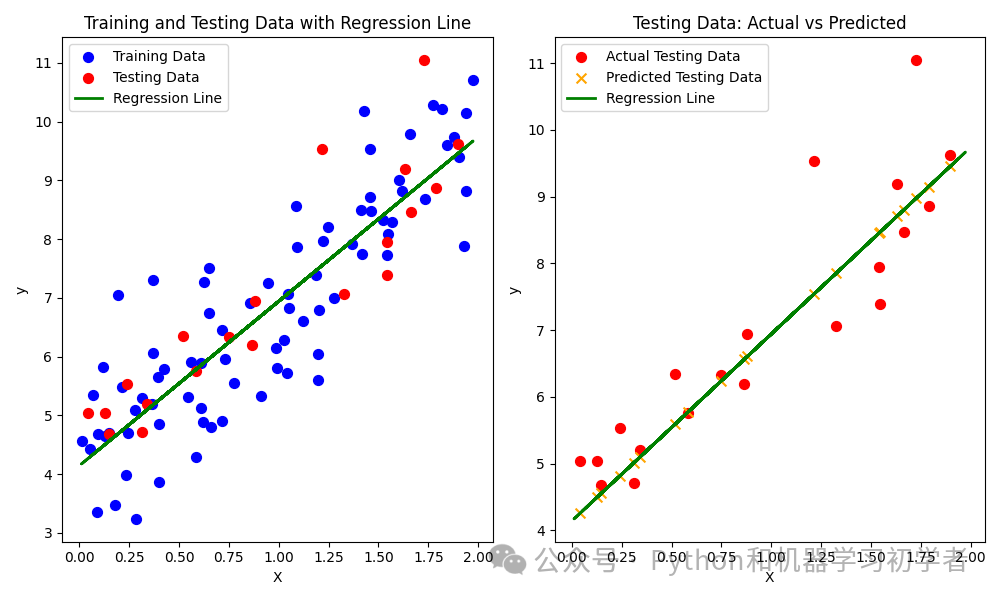
图1：展示了训练集（蓝色点）、测试集（红色点）以及基于训练集的回归拟合线（绿色线）。这有助于观察模型对训练数据的拟合情况。
图2：展示了测试集的实际值（红色点）和预测值（橙色叉号），并再次绘制了回归拟合线。这帮助分析模型在测试集上的预测性能。

8. 数据增强 (Data Augmentation)

8.1 图像数据增强 (Image Data Augmentation)

原理

通过旋转、缩放、裁剪等方法生成更多的图像样本，增加数据的多样性，提高模型的泛化能力。

方法

常用方法包括随机裁剪、水平/垂直翻转、颜色抖动、仿射变换等。

8.2 文本数据增强 (Text Data Augmentation)

原理

通过同义词替换、词序交换、随机插入/删除等方法生成更多的文本样本。

方法

数据增强的目的是通过生成不同的样本来增强模型的鲁棒性，并且避免过拟合。

Python案例

生成一个虚拟的 2D 点数据集，并模拟对这些点进行不同方式的数据增强（旋转和翻转）。最终绘制增强前后的数据分布图，同时使用 Seaborn 进行密度分布（KDE）绘制。

import numpy as np   import matplotlib.pyplot as plt   import seaborn as sns   from sklearn.preprocessing import MinMaxScaler      # 设置随机种子   np.random.seed(42)      # 生成虚拟数据集：2D 正态分布   mean = [5, 5]   cov = [[1, 0.5], [0.5, 1]]  # 协方差矩阵   data = np.random.multivariate_normal(mean, cov, 500)      # 数据增强：1. 图像翻转（左右翻转）   def flip_horizontal(data):       flipped_data = data.copy()       flipped_data[:, 0] = -flipped_data[:, 0]  # 反转x轴       return flipped_data      # 数据增强：2. 图像旋转（旋转角度为45度）   def rotate(data, angle_degrees):       angle_radians = np.deg2rad(angle_degrees)       rotation_matrix = np.array([[np.cos(angle_radians), -np.sin(angle_radians)],                                   [np.sin(angle_radians), np.cos(angle_radians)]])       rotated_data = np.dot(data, rotation_matrix)       return rotated_data      # 进行数据增强   flipped_data = flip_horizontal(data)   rotated_data = rotate(data, 45)      # 数据缩放到[0, 1]范围以便可视化   scaler = MinMaxScaler()   data_scaled = scaler.fit_transform(data)   flipped_data_scaled = scaler.transform(flip_horizontal(data))   rotated_data_scaled = scaler.transform(rotate(data, 45))      # 创建子图   fig, axs = plt.subplots(2, 2, figsize=(12, 12))      # 原始数据分布   sns.scatterplot(x=data_scaled[:, 0], y=data_scaled[:, 1], ax=axs[0, 0], s=50, color='blue', label='Original Data')   sns.kdeplot(x=data_scaled[:, 0], y=data_scaled[:, 1], ax=axs[0, 0], cmap='Blues', fill=True, alpha=0.4)   axs[0, 0].set_title('Original Data Distribution', fontsize=14)   axs[0, 0].legend()      # 翻转后的数据分布   sns.scatterplot(x=flipped_data_scaled[:, 0], y=flipped_data_scaled[:, 1], ax=axs[0, 1], s=50, color='green', label='Flipped Data')   sns.kdeplot(x=flipped_data_scaled[:, 0], y=flipped_data_scaled[:, 1], ax=axs[0, 1], cmap='Greens', fill=True, alpha=0.4)   axs[0, 1].set_title('Horizontally Flipped Data', fontsize=14)   axs[0, 1].legend()      # 旋转后的数据分布   sns.scatterplot(x=rotated_data_scaled[:, 0], y=rotated_data_scaled[:, 1], ax=axs[1, 0], s=50, color='red', label='Rotated Data (45°)')   sns.kdeplot(x=rotated_data_scaled[:, 0], y=rotated_data_scaled[:, 1], ax=axs[1, 0], cmap='Reds', fill=True, alpha=0.4)   axs[1, 0].set_title('Rotated Data (45°)', fontsize=14)   axs[1, 0].legend()      # 三种数据的对比   sns.scatterplot(x=data_scaled[:, 0], y=data_scaled[:, 1], ax=axs[1, 1], s=50, color='blue', label='Original Data', alpha=0.6)   sns.scatterplot(x=flipped_data_scaled[:, 0], y=flipped_data_scaled[:, 1], ax=axs[1, 1], s=50, color='green', label='Flipped Data', alpha=0.6)   sns.scatterplot(x=rotated_data_scaled[:, 0], y=rotated_data_scaled[:, 1], ax=axs[1, 1], s=50, color='red', label='Rotated Data', alpha=0.6)   axs[1, 1].set_title('Comparison of Augmented Data', fontsize=14)   axs[1, 1].legend()      # 设置子图间距   plt.tight_layout()   plt.show()

1. 生成虚拟数据：生成了一个500个点的2D正态分布数据集。

2. 数据增强：

进行了水平翻转（左右反转 x 轴数据）。
进行了45度旋转。

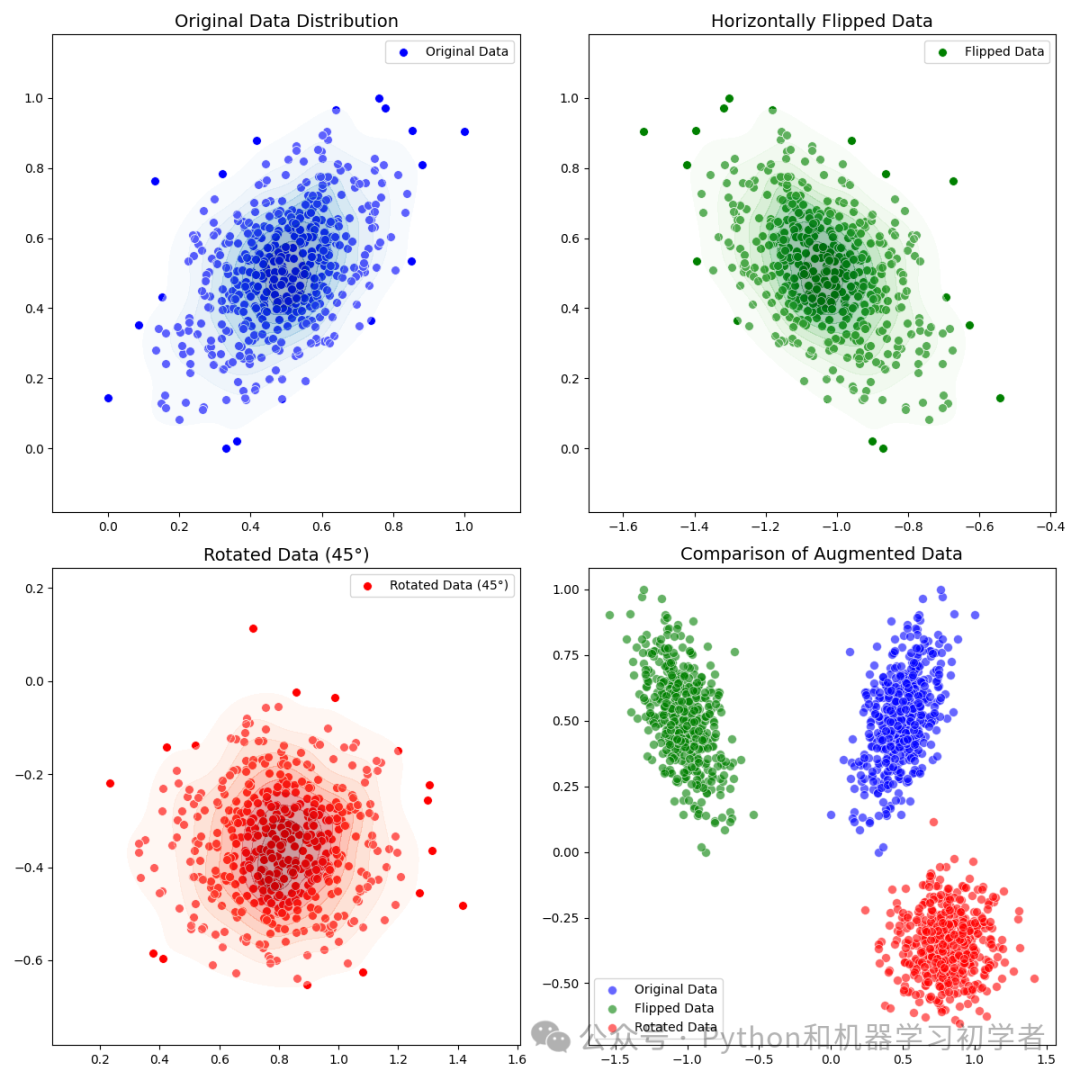
原始数据的散点图和密度分布。
水平翻转后的数据的散点图和密度分布。
旋转后的数据的散点图和密度分布。
最后对比展示原始数据、翻转数据和旋转数据的散点图。

9. 数据平衡 (Data Balancing)

9.1 欠采样 (Under-sampling)

原理

通过减少多数类样本的数量，使得类别分布更加平衡。

方法

随机删除多数类样本，或选择性保留代表性样本。

9.2 过采样 (Over-sampling)

原理

通过增加少数类样本的数量，使得类别分布更加平衡。

方法

常用方法包括随机复制少数类样本、SMOTE算法（合成少数类样本）等。

Python案例

使用虚拟数据集进行数据平衡的案例，针对 分类不平衡问题。在这个例子中，我们生成一个分类不平衡的数据集，随后使用 过采样 (Oversampling) 和 欠采样 (Undersampling) 方法对数据进行平衡，最后展示不同阶段的类别分布。

import numpy as np   import pandas as pd   import matplotlib.pyplot as plt   from imblearn.over_sampling import RandomOverSampler   from imblearn.under_sampling import RandomUnderSampler   from collections import Counter      # 设置随机种子，保证结果可重复   np.random.seed(42)      # 生成虚拟数据集 (不平衡)   # 类别 0 占 90%，类别 1 占 10%   X = np.random.randn(1000, 2)  # 两个特征   y = np.hstack([np.zeros(900), np.ones(100)])      # 打印原始数据类别分布   print("原始数据分布:", Counter(y))      # 欠采样   undersampler = RandomUnderSampler(sampling_strategy='majority', random_state=42)   X_under, y_under = undersampler.fit_resample(X, y)      # 打印欠采样后类别分布   print("欠采样后数据分布:", Counter(y_under))      # 过采样   oversampler = RandomOverSampler(sampling_strategy='minority', random_state=42)   X_over, y_over = oversampler.fit_resample(X, y)      # 打印过采样后类别分布   print("过采样后数据分布:", Counter(y_over))      # 画图 - 原始数据、欠采样后数据、过采样后数据的对比   fig, axes = plt.subplots(1, 3, figsize=(18, 6), sharex=True, sharey=True)      # 原始数据分布   axes[0].scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='red', label='Class 0', alpha=0.6)   axes[0].scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='blue', label='Class 1', alpha=0.6)   axes[0].set_title("Original Data")   axes[0].legend()   axes[0].set_xlabel('Feature 1')   axes[0].set_ylabel('Feature 2')      # 欠采样后的数据分布   axes[1].scatter(X_under[y_under == 0][:, 0], X_under[y_under == 0][:, 1], color='red', label='Class 0', alpha=0.6)   axes[1].scatter(X_under[y_under == 1][:, 0], X_under[y_under == 1][:, 1], color='blue', label='Class 1', alpha=0.6)   axes[1].set_title("After Undersampling")   axes[1].legend()   axes[1].set_xlabel('Feature 1')      # 过采样后的数据分布   axes[2].scatter(X_over[y_over == 0][:, 0], X_over[y_over == 0][:, 1], color='red', label='Class 0', alpha=0.6)   axes[2].scatter(X_over[y_over == 1][:, 0], X_over[y_over == 1][:, 1], color='blue', label='Class 1', alpha=0.6)   axes[2].set_title("After Oversampling")   axes[2].legend()   axes[2].set_xlabel('Feature 1')      # 设置图形的标题和显示   plt.suptitle("Comparison of Class Distributions Before and After Sampling", fontsize=16)   plt.tight_layout()   plt.show()

数据生成：使用 np.random.randn 生成了1000个样本，类别0和类别1的比例分别是90%和10%，表示数据集不平衡。
欠采样 (Undersampling)：使用 RandomUnderSampler 对类别0进行欠采样，使得类别0和类别1样本数量相等。
过采样 (Oversampling)：使用 RandomOverSampler 对类别1进行过采样，使得类别0和类别1样本数量相等。

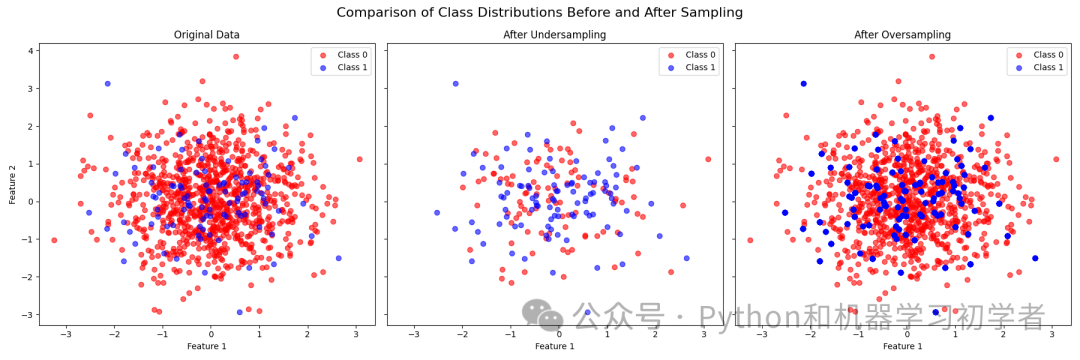
10. 数据转换 (Data Transformation)

10.1 特征构造 (Feature Engineering)

原理

基于现有特征组合、变换、提取新的特征，以增强模型的表达能力。

方法

特征组合、离散化、交互特征、时间特征提取等。

10.2 非线性变换

原理

通过平方、平方根、对数等操作处理特征与标签之间的非线性关系。

方法与公式

对于非线性关系，非线性变换能够提升模型拟合能力。

Python案例

案例展示了标准化（Standardization）和归一化（Normalization）两种常见的数据转换方法，并分别绘制出转换前和转换后的数据分布图。虚拟数据集将使用正态分布生成。

import numpy as np   import pandas as pd   import matplotlib.pyplot as plt   from sklearn.preprocessing import StandardScaler, MinMaxScaler      # 生成虚拟数据集   np.random.seed(42)   data = pd.DataFrame({       'Feature1': np.random.normal(loc=0, scale=1, size=100),  # 正态分布数据       'Feature2': np.random.rand(100) * 100  # 随机生成 [0, 100] 区间数据   })      # 创建标准化和归一化的转换器   scaler_standard = StandardScaler()   scaler_minmax = MinMaxScaler()      # 对数据进行标准化   data_standardized = scaler_standard.fit_transform(data)   data_standardized = pd.DataFrame(data_standardized, columns=data.columns)      # 对数据进行归一化   data_normalized = scaler_minmax.fit_transform(data)   data_normalized = pd.DataFrame(data_normalized, columns=data.columns)      # 绘图设置   plt.figure(figsize=(12, 8))      # 原始数据分布   plt.subplot(3, 2, 1)   plt.hist(data['Feature1'], bins=20, color='blue', alpha=0.7, label='Feature1')   plt.title('Original Feature1 Distribution', fontsize=12)   plt.legend()      plt.subplot(3, 2, 2)   plt.hist(data['Feature2'], bins=20, color='green', alpha=0.7, label='Feature2')   plt.title('Original Feature2 Distribution', fontsize=12)   plt.legend()      # 标准化后数据分布   plt.subplot(3, 2, 3)   plt.hist(data_standardized['Feature1'], bins=20, color='red', alpha=0.7, label='Standardized Feature1')   plt.title('Standardized Feature1 Distribution', fontsize=12)   plt.legend()      plt.subplot(3, 2, 4)   plt.hist(data_standardized['Feature2'], bins=20, color='orange', alpha=0.7, label='Standardized Feature2')   plt.title('Standardized Feature2 Distribution', fontsize=12)   plt.legend()      # 归一化后数据分布   plt.subplot(3, 2, 5)   plt.hist(data_normalized['Feature1'], bins=20, color='purple', alpha=0.7, label='Normalized Feature1')   plt.title('Normalized Feature1 Distribution', fontsize=12)   plt.legend()      plt.subplot(3, 2, 6)   plt.hist(data_normalized['Feature2'], bins=20, color='pink', alpha=0.7, label='Normalized Feature2')   plt.title('Normalized Feature2 Distribution', fontsize=12)   plt.legend()      # 调整布局   plt.tight_layout()   plt.show()

虚拟数据集生成：Feature1 是一个正态分布的数据，而 Feature2 是在 [0, 100] 之间的均匀随机分布数据。
标准化与归一化：标准化：使用 StandardScaler 将数据转化为均值为0，标准差为1的分布。归一化：使用 MinMaxScaler 将数据映射到 [0, 1] 范围内。

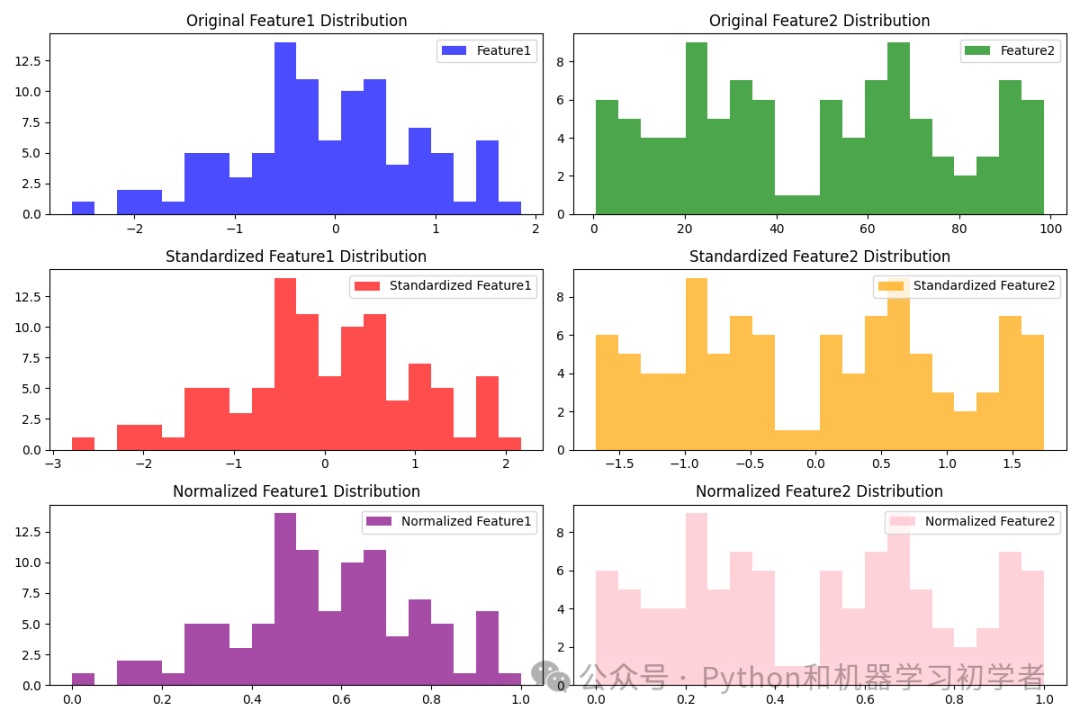
原始数据的分布图（Feature1 和 Feature2）
标准化后的数据分布图
归一化后的数据分布图

如何学习大模型 AI ？

由于新岗位的生产效率，要优于被取代岗位的生产效率，所以实际上整个社会的生产效率是提升的。

但是具体到个人，只能说是：

“最先掌握AI的人，将会比较晚掌握AI的人有竞争优势”。

这句话，放在计算机、互联网、移动互联网的开局时期，都是一样的道理。

我在一线互联网企业工作十余年里，指导过不少同行后辈。帮助很多人得到了学习和成长。

我意识到有很多经验和知识值得分享给大家，也可以通过我们的能力和经验解答大家在人工智能学习中的很多困惑，所以在工作繁忙的情况下还是坚持各种整理和分享。但苦于知识传播途径有限，很多互联网行业朋友无法获得正确的资料得到学习提升，故此将并将重要的AI大模型资料包括AI大模型入门学习思维导图、精品AI大模型学习书籍手册、视频教程、实战学习等录播视频免费分享出来。

在这里插入图片描述