当然,如果你对 TensorFlow 1.x 本来就不熟悉,可能无法看明白这些升级的内容。不用担心,本次直接对 TensorFlow 2 进行学习,我们不再回首过去,直接展望未来。
接下来,我们将从 TensorFlow 基础概念语法入手,一步一步学习 TensorFlow 的使用。
建议先学习 Python 数值计算库 NumPy 的使用,能帮助你更清楚地理解 TensorFlow 2 中的一些函数用法和概念。
=================================================================
张量,如果你第一次听说,一定会感觉到它是一个很厉害的东西吧。它的确很厉害,但是不难理解。
张量的概念贯穿于物理学和数学中,如果你去看它的很多理论描述,可能并不那么浅显易懂。例如,下面有两种关于 张量的定义:
-
通常定义张量的物理学或传统数学方法,是把张量看成一个多维数组,当变换坐标或变换基底时,其分量会按照一定规则进行变换,这些规则有两种:即协变或逆变转换。
-
通常现代数学中的方法,是把张量定义成某个矢量空间或其对偶空间上的多重线性映射,这矢量空间在需要引入基底之前不固定任何坐标系统。例如协变矢量,可以描述为 1-形式,或者作为逆变矢量的对偶空间的元素。
上面的定义不知道你看懂了没有?估计会有点困难。下面,我们进行通俗易懂的说明:
首先,你应该知道什么是向量和矩阵。先前的介绍中,我们把 1 维的数组称之为向量,2维的数组称之为矩阵。那么,现在告诉你张量其实代表着更大的范围,你也可以把其看作是 N 维数组。
所以,如果现在重新描述向量和矩阵,就可以是:
一阶张量为向量,二阶张量为矩阵。当然,零阶张量也就是标量,而更重要的是 N 阶张量,也就是 N 维数组。
| 阶 | 数学实例 |
| :-: | :-: |
| 0 | 标量(只有大小) |
| 1 | 矢量(大小和方向) |
| 2 | 矩阵(数据表) |
| 3 | 3 阶张量(数据立体) |
| N | N 阶张量(自行想象) |
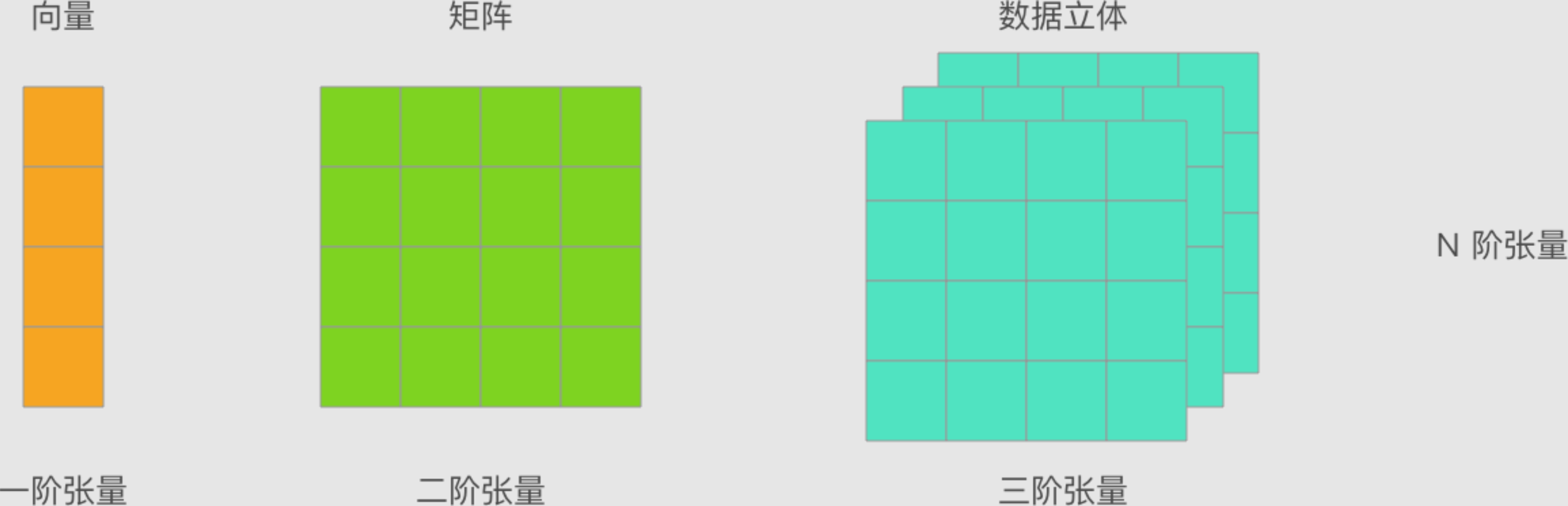
所以,张量并不是什么晦涩难懂的概念。如果不严谨的讲,张量就是 N 维数组。前面提到的向量、矩阵,也是张量。
你即将了解到的大多数深度学习框架都会使用张量的概念,这样做的好处是统一对数据的定义。NumPy 中,数据都使用 Ndarray 多维数组进行定义,TensorFlow 中,数据都会用张量进行表述。
下面就来了解 TensorFlow 中对张量的定义。
在 TensorFlow 中,每一个 Tensor 都具备两个基础属性:
-
数据类型(默认:float32)
-
形状
其中,数据类型大致如下表所示:
| Tensor 类型 | 描述 |
| :-: | :-: |
| tf.float32 | 32 位浮点数 |
| tf.float64 | 64 位浮点数 |
| tf.int64 | 64 位有符号整型 |
| tf.int32 | 32 位有符号整型 |
| tf.int16 | 16 位有符号整型 |
| tf.int8 | 8 位有符号整型 |
| tf.uint8 | 8 位无符号整型 |
| tf.string | 可变长度的字节数组 |
| tf.bool | 布尔型 |
| tf.complex64 | 实数和虚数 |
另外,TensorFlow 通过三种符号约定来描述张量维度:阶,形状和维数。
三者之间的关系如下:
| 形状 | 阶 | 维数 | 示例 |
| :-: | :-: | :-: | :-: |
| [] | 0 | 0-D | 0 维张量。标量。 |
| [D0] | 1 | 1-D | 形状为 [5] 的 1 维张量。 |
| [D0, D1] | 2 | 2-D | 形状为 [3, 4] 的 2 维张量。 |
| [D0, D1, D2] | 3 | 3-D | 形状为 [1, 4, 3] 的 3 维张量。 |
| [D0, D1, … Dn-1] | n | n-D | 形状为 [D0, D1, … Dn-1] 的张量。 |
值得注意的是,上表中的示例都是形容张量的形状。例如 [3, 4] 指的张量的形状为 [3, 4],而不是张量 [3, 4]。
根据不同的用途,TensorFlow 中主要有 2 种张量类型,分别是:
-
tf.Variable:变量 Tensor,需要指定初始值,常用于定义可变参数,例如神经网络的权重。 -
tf.constant:常量 Tensor,需要指定初始值,定义不变化的张量。
我们可以通过传入列表或 NumPy 数组来新建变量和常量类型的张量
(1)查看 TensorFlow 版本:

(2)定义形状为 (3, 3) 的二维变量:

(3)定义现状为 (2,2) 二维常量

仔细观察,你会发现输出包含了张量的 3 部分属性,分别是
-
形状
shape -
数据类型
dtype, -
对应的 NumPy 数组。
你还可以直接通过 .numpy() 输出张量的 NumPy 数组。

上面我们已经介绍了常量张量,这里再列举几个经常会用到的新建特殊常量张量的方法:
-
tf.zeros:新建指定形状且全为 0 的常量 Tensor -
tf.zeros_like:参考某种形状,新建全为 0 的常量 Tensor -
tf.ones:新建指定形状且全为 1 的常量 Tensor -
tf.ones_like:参考某种形状,新建全为 1 的常量 Tensor -
tf.fill:新建一个指定形状且全为某个标量值的常量 Tensor
(1)3x3 全为 0 的常量 Tensor

(2)c 形状一致全为 1 的常量 Tensor

(3)2x3 全为 6 的常量 Tensor

除此之外,我们还可以创建一些序列,例如:
-
tf.linspace:创建一个等间隔序列。 -
tf.range:创建一个数字序列。


实际上,如果你熟悉 NumPy 的话,你会发现这与 NumPy 中创建各式各样的多维数组方法大同小异。数据类型是一切的基础,了解完张量我们就可以继续学习张量的运算了。
TensorFlow 2 带来的最大改变之一是将 1.x 的 Graph Execution(图与会话机制)更改为 Eager Execution(动态图机制)。在 1.x 版本中,低级别 TensorFlow API 首先需要定义数据流图,然后再创建 TensorFlow 会话,这一点在 2.0 中被完全舍弃。
TensorFlow 2 中的 Eager Execution 是一种命令式编程环境,可立即评估操作,无需构建图。
所以说,TensorFlow 的张量运算过程可以像 NumPy 一样直观且自然了。接下来,我们以最简单的加法运算为例:

如果你接触过 1.x 版本的 TensorFlow,你要知道一个加法运算过程十分复杂。我们需要初始化全局变量 → 建立会话 → 执行计算,最终才能打印出张量的运算结果。
init_op = tf.global_variables_initializer() # 初始化全局变量
with tf.Session() as sess: # 启动会话
最后
自我介绍一下,小编13年上海交大毕业,曾经在小公司待过,也去过华为、OPPO等大厂,18年进入阿里一直到现在。
深知大多数初中级Android工程师,想要提升技能,往往是自己摸索成长,自己不成体系的自学效果低效漫长且无助。
因此收集整理了一份《2024年Web前端开发全套学习资料》,初衷也很简单,就是希望能够帮助到想自学提升又不知道该从何学起的朋友,同时减轻大家的负担。

既有适合小白学习的零基础资料,也有适合3年以上经验的小伙伴深入学习提升的进阶课程,基本涵盖了95%以上Android开发知识点!不论你是刚入门Android开发的新手,还是希望在技术上不断提升的资深开发者,这些资料都将为你打开新的学习之门!
如果你觉得这些内容对你有帮助,需要这份全套学习资料的朋友可以戳我获取!!
由于文件比较大,这里只是将部分目录截图出来,每个节点里面都包含大厂面经、学习笔记、源码讲义、实战项目、讲解视频,并且会持续更新!
…(img-bOFK08p7-1715621245439)]
[外链图片转存中…(img-j5ryQnVd-1715621245439)]
既有适合小白学习的零基础资料,也有适合3年以上经验的小伙伴深入学习提升的进阶课程,基本涵盖了95%以上Android开发知识点!不论你是刚入门Android开发的新手,还是希望在技术上不断提升的资深开发者,这些资料都将为你打开新的学习之门!
如果你觉得这些内容对你有帮助,需要这份全套学习资料的朋友可以戳我获取!!
由于文件比较大,这里只是将部分目录截图出来,每个节点里面都包含大厂面经、学习笔记、源码讲义、实战项目、讲解视频,并且会持续更新!





















 981
981

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








