逻辑回归
一、介绍
1.什么是线性回归
线性回归
利用大量的样本
(
x
i
,
y
i
)
i
=
1
N
\left ( x_{i} ,y_{i} \right )_{i=1}^{N}
(xi,yi)i=1N,通过有监督的学习,学习到由x到y的映射f,利用该映射关系对未知的数据进行预估,因为y为连续值,所以是回归问题。
- 单变量情况
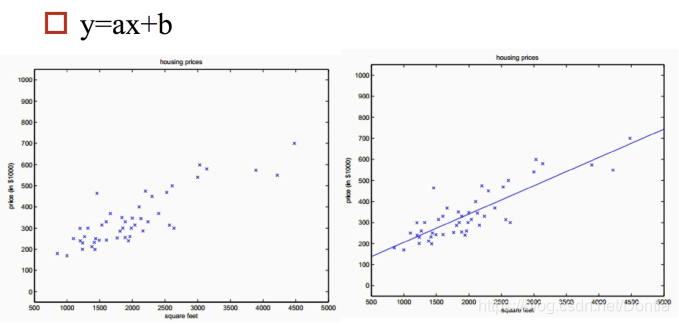
- 多变量情况:二维空间的直线,转化为高维空间的平面
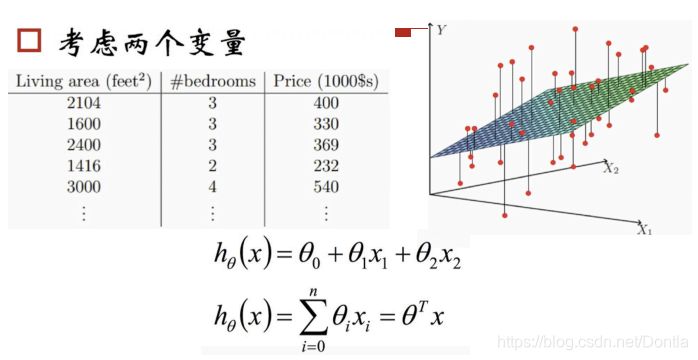
线性回归的表达式
-
假设函数
线性回归的假设函数
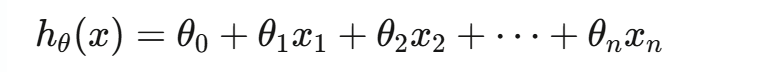
-
优化方法
监督学习的优化方法=损失函数+对损失函数的优化 -
损失函数
如何衡量已有的参数 θ \theta θ的好坏?
利用损失函数来衡量,损失函数度量预测值和标准答案的偏差,不同的参数有不同的偏差,所以要通过最小化损失函数,也就是最小化偏差来得到最好的参数。
输出函数: h 0 ( x ) h_{0}(x) h0(x)
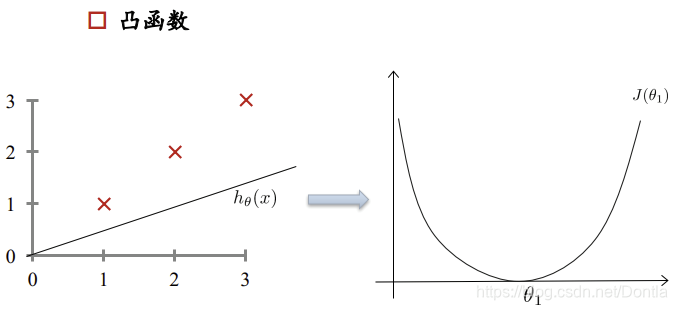
损失函数:凸函数
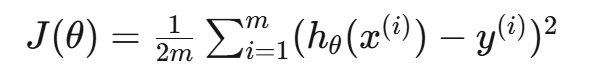
解释:因为有m个样本,所以要平均,分母的2是为了求导方便 -
损失函数的优化
损失函数如下图所示,是一个凸函数,我们的目的是达到最低点,也就是损失函数最小。
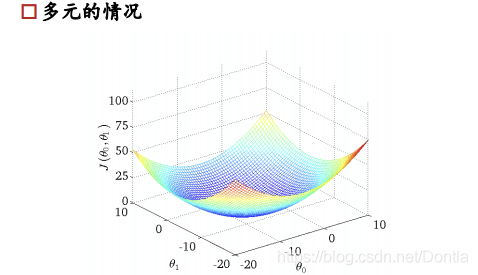
多元情况下容易出现局部极值
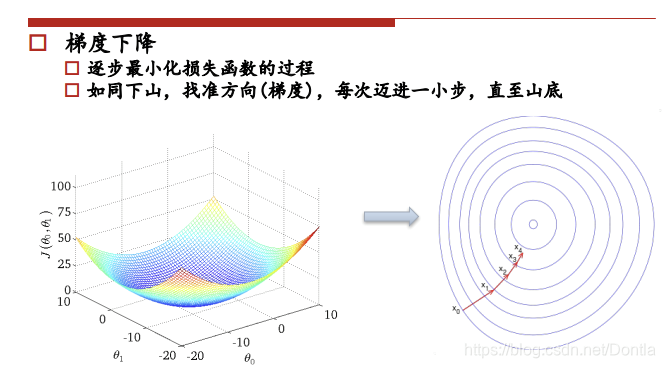
求极值的数学思想,对公式求导=0即可得到极值,但是工业上计算量很大,公式很复杂,所以从计算机的角度来讲,求极值是利用梯度下降法。
梯度下降
2.从线性回归到逻辑回归的引入
- 线性回归可以预测连续值,但是不能解决分类问题,我们需要根据预测的结果判定其属于正类还是负类。所以逻辑回归就是将线性回归的 ( − ∞ , + ∞ ) \left ( -\infty ,+\infty \right ) (−∞,+∞)的结果,通过sigmoid函数映射到(0,1)之间。
3.什么是逻辑回归
-
监督学习,解决二分类问题。
-
分类的本质:在空间中找到一个决策边界来完成分类的决策。
-
线性回归决策函数: h θ ( x ) = θ T x h_{\theta }\left ( x \right )=\theta ^{T}x hθ(x)=θTx
-
将其通过sigmoid函数 S i g m o i d ( x ) = 1 1 + e − x Sigmoid\left ( x \right )=\frac{1}{1+e^{-x}} Sigmoid(x)=1+e−x1,获得逻辑回归的决策函数: h θ ( x ) = 1 1 + e − θ T x h_{\theta }\left ( x \right )=\frac{1}{1+e^{-\theta ^{T}x}} hθ(x)=1+e−θTx1
为什么使用sigmoid函数
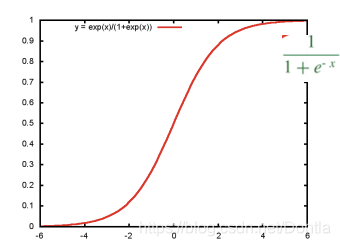
① 可以对
(
−
∞
,
+
∞
)
\left ( -\infty ,+\infty \right )
(−∞,+∞)的结果映射到(0,1)之间,作为概率。
- 当 z → − ∞ , h θ ( x ) → 0 z\rightarrow -\infty ,h_{\theta }\left ( x \right )\rightarrow 0 z→−∞,hθ(x)→0;
- 当 z → + ∞ , h θ ( x ) → 1 z\rightarrow +\infty ,h_{\theta }\left ( x \right )\rightarrow 1 z→+∞,hθ(x)→1
② 容易得到决策边界( 可以将0.5作为决策边界)
- 当 x < 0 时,sigmoid(x) < 0.5;
- 当 x > 0 时,sigmoid(x) > 0.5
③ 数学特性好,求导容易: g ′ ( z ) = g ( z ) ⋅ ( 1 − g ( z ) ) g^{'}\left ( z \right )=g\left ( z \right )·\left ( 1-g\left ( z \right ) \right ) g′(z)=g(z)⋅(1−g(z))

对数几率回归
将Sigmoid函数代入线性回归函数模型,得到
y
=
1
1
+
e
−
(
ω
T
X
+
b
)
y=\frac{1}{1+e^{-\left (\omega ^{T}X+b \right )}}
y=1+e−(ωTX+b)1
进一步得到
l
n
y
1
−
y
=
ω
T
X
+
b
ln\frac{y}{1-y}=\omega ^{T}X+b
ln1−yy=ωTX+b
将 y 视为样本 x 作为正例的概率,则 1-y 则作为 x 作为反例的概率。两者比值为
y
1
−
y
\frac{y}{1-y}
1−yy,因此
l
n
y
1
−
y
ln\frac{y}{1-y}
ln1−yy被称为对数几率。进一步
l
n
p
(
y
=
1
∣
x
)
p
(
y
=
0
∣
x
)
=
ω
T
X
+
b
ln\frac{p\left ( y=1|x \right )}{p\left ( y=0|x \right )}=\omega ^{T}X+b
lnp(y=0∣x)p(y=1∣x)=ωTX+b。就可以推导出
P
(
Y
=
1
∣
X
)
=
1
1
+
e
−
ω
T
X
+
b
P(Y=1|X)=\frac{1}{1+e^{-\omega ^{T}X+b}}
P(Y=1∣X)=1+e−ωTX+b1
P
(
Y
=
0
∣
X
)
=
1
1
+
e
ω
T
X
+
b
P(Y=0|X)=\frac{1}{1+e^{\omega ^{T}X+b}}
P(Y=0∣X)=1+eωTX+b1
逻辑回归的输出是事件发生的概率,而不是直接的分类标签。输出概率可以解释为某个事件属于类1的可能性。
例如:
- 若 P ( y = 1 ∣ x ) = 0.8 P(y=1|x)=0.8 P(y=1∣x)=0.8,表示在给定输入特征 x x x的情况下,事件 y = 1 y=1 y=1发生的概率为80%。
- 若 P ( y = 1 ∣ x ) = 0.2 P(y=1|x)=0.2 P(y=1∣x)=0.2,则表示事件 y = 1 y=1 y=1发生的概率为20%,所以将其分为类0。
这一概率解释是逻辑回归的一个重要特征,它不仅给出一个分类结果,还提供了分类的置信度,从而能够在决策过程中提供更多的信息。例如:在某些应用中,可以根据应用场景调整决策阈值,而不仅仅依赖默认的0.5阈值。
逻辑回归的损失函数
线性回归的损失函数为平方损失函数,如果将其用于逻辑回归的损失函数,则其数学特性不好,有很多局部极小值,难以用梯度下降法求最优。
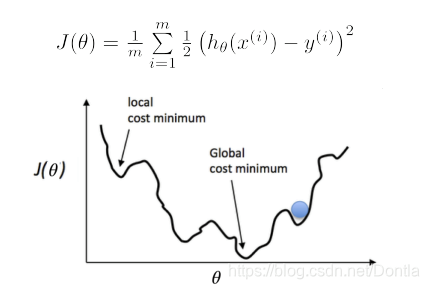
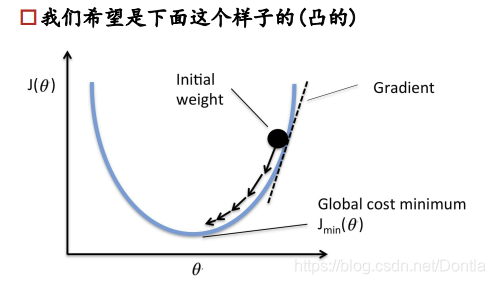
所以我们在逻辑回归中用的损失函数为对数损失函数(最小化负的对数似然函数,也称为交叉熵损失)。
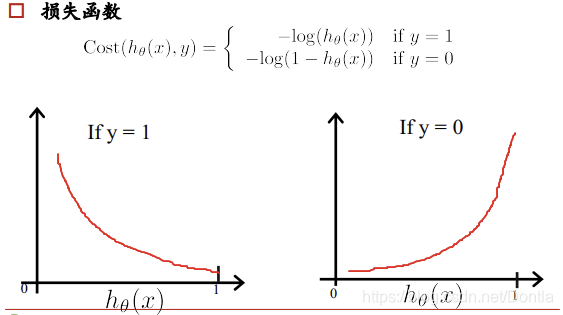
其中,y为真实值,
h
θ
(
x
)
h_{\theta }\left ( x \right )
hθ(x)为预测值,损失函数值越小越好。
当 y = 1 时,
h
θ
(
x
)
h_{\theta }\left ( x \right )
hθ(x)的值越大越好;当 y =0 时,
h
θ
(
x
)
h_{\theta }\left ( x \right )
hθ(x)的值越小越好。
所以完整的损失函数为:
c
o
s
t
(
h
θ
(
x
)
,
y
)
=
∑
i
=
1
m
−
y
i
l
o
g
(
h
θ
(
x
)
)
−
(
1
−
y
i
)
l
o
g
(
1
−
h
θ
(
x
)
)
cost(h_{\theta }\left ( x \right ),y)= \sum_{i=1}^{m}-y_{i}log(h_{\theta }\left ( x \right ))-(1-y_{i})log(1-h_{\theta }(x))
cost(hθ(x),y)=i=1∑m−yilog(hθ(x))−(1−yi)log(1−hθ(x))
其中
h
θ
(
x
)
h_{\theta }\left ( x \right )
hθ(x)是样本 x 属于正类的概率。
优化的目标就是找到参数
θ
\theta
θ 是的损失函数最小。
解释:
如果一个样本为正样本,那么我们希望将其预测为正样本的概率 p 越大越好,也就是决策函数的值越大越好,则
log
p
\log p
logp 越大越好,逻辑回归的决策函数值就是样本为正的概率;
如果一个样本为负样本,那么我们希望将其预测的负样本的概率越大越好,也就是(1-p)越大越好,即
log
(
1
−
p
)
\log (1-p)
log(1−p)越大越好。
逻辑回归的本质:在线性回归的基础上加了一个Sigmoid映射,将连续输出变为概率,从而实现分类的能力。
梯度下降法
梯度下降法是逻辑回归模型中常用的优化算法之一,用于最小化损失函数,找到能够最小化损失函数的参数值
β
\beta
β 。其基本思想是沿着损失函数的负梯度方向更新模型参数,逐步接近最优解。
梯度下降法的参数更新公式为:
θ
j
=
θ
j
−
α
∂
J
(
θ
)
∂
θ
j
\theta _{j}=\theta _{j}-\alpha \frac{\partial J\left ( \theta \right )}{\partial\theta _{j}}
θj=θj−α∂θj∂J(θ)
其中:
- θ j \theta _{j} θj是模型的第j个参数。
- α \alpha α 是学习率(步长),控制每次更新的幅度。
- ∂ J ( θ ) ∂ θ j \frac{\partial J(\theta )}{\partial \theta _{j}} ∂θj∂J(θ) 是损失函数关于参数 θ j \theta _{j} θj的偏导数,称为梯度。
对于学习率(步长) α \alpha α:
① 如果 α \alpha α 太大,可能出现无法找到最优值的情况
② 如果 α \alpha α 太小,可能会陷入局部最优
每次迭代时,模型的参数根据损失函数的梯度进行调整,直到损失函数收敛到最小值。
逻辑回归的优缺点
✅ 优点
模型简单、易于实现
输出概率、解释性强
可处理非线性特征(通过特征转换或多项式项)
适合线性可分问题
❌ 缺点
不能处理复杂非线性关系(需借助特征工程或换模型)
对异常值敏感
容易欠拟合
4.逻辑回归与线性回归的联系
逻辑回归其本质还是线性回归,它仅在线性回归的基础上,在特征到结果的映射中加入了一层sigmoid函数映射来达到拟合非线性数据的功能。
一、假设函数不同
1.逻辑函数的假设函数是sigmoid函数
2.线性回归的则是线性函数
二、性质不同
1.逻辑回归:是一种广义的线性回归分析模型。
2.线性回归:利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。
三、应用不同
1.逻辑回归:常用于数据挖掘,疾病自动诊断,经济预测等领域。
2.线性回归:常运用于数学、金融、趋势线、经济学等领域。
二、代码实现
1.Logistic回归的过程
① 数据加载和预处理
② 定义Sigmoid激活函数
③ 定义代价函数并选择优化算法
④ 训练模型并获取权重
⑤ 可视化结果
2.加载数据
- 功能:读取数据文件,每一行是一个样本,格式为 x1 x2 label;
- 每一行被拆成 x1, x2 特征和一个标签 label;
- 在特征前添加常数 1.0,用于表示偏置 w0,简化运算;
- 最终返回:
dataMat: 一个二维数组(样本 × 特征);
labelMat: 标签数组。
def loadDataSet():
dataMat = []
labelMat = []
with open("testSet1.txt") as fr:
for line in fr.readlines():
lineArr = line.strip().split()
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) # 添加偏置项X0 = 1
labelMat.append(int(lineArr[2]))
return dataMat, labelMat
3.Sigmoid函数
- Sigmoid 是逻辑回归的激活函数,将输入 inX 压缩到 (0,1) 区间;
- 输出代表样本属于“正类”的概率。
数学公式: σ ( x ) = 1 1 + e − x \sigma \left ( x \right )=\frac{1}{1+e^{-x}} σ(x)=1+e−x1
def sigmoid(inX):
return 1.0 / (1 + np.exp(-inX))
4.批量梯度下降法训练逻辑回归
-
输入:
dataMatIn: 特征矩阵(m × n);
classLabels: 标签向量(m × 1);
alpha: 学习率;
maxCycles: 迭代次数; -
每轮迭代做:
1 .计算预测值 h = sigmoid(XW)
2 .计算预测误差 h - y
3 .更新权重:
w : = w − α ⋅ X T ( h − y ) w:=w-\alpha· X^{T}\left ( h-y \right ) w:=w−α⋅XT(h−y) -
返回最终训练好的权重向量。
def gradDescent(dataMatIn, classLabels, alpha=0.001, maxCycles=500):
dataMatrix = np.array(dataMatIn)
labelMat = np.array(classLabels).reshape(-1, 1) # 转成列向量
m, n = dataMatrix.shape
weights = np.ones((n, 1)) # 初始化权重为1
for k in range(maxCycles):
h = sigmoid(np.dot(dataMatrix, weights)) # 预测输出:m×1
error = h - labelMat # 预测误差:m×1
weights = weights - alpha * np.dot(dataMatrix.T, error) # 梯度更新
return weights
5.绘制分类边界
- 将正负类用不同颜色表示;
- 决策边界是:
w 0 + w 1 x 1 + w 2 x 2 = 0 ⇒ x 2 = − w 0 − w 1 x 1 w 2 w_{0}+w_{1}x_{1}+w_{2}x_{2}=0\Rightarrow x_{2}=\frac{-w_{0}-w_{1}x_{1}}{w_{2}} w0+w1x1+w2x2=0⇒x2=w2−w0−w1x1 - 用 matplotlib 画出这条线。
def plotBestFit(weights):
dataMat, labelMat = loadDataSet()
dataArr = np.array(dataMat)
n = dataArr.shape[0]
xcord1 = []; ycord1 = []
xcord2 = []; ycord2 = []
for i in range(n):
if int(labelMat[i]) == 1:
xcord1.append(dataArr[i, 1])
ycord1.append(dataArr[i, 2])
else:
xcord2.append(dataArr[i, 1])
ycord2.append(dataArr[i, 2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s', label="Class 1")
ax.scatter(xcord2, ycord2, s=30, c='green', label="Class 0")
x = np.arange(-3.0, 3.0, 0.1)
y = (-weights[0] - weights[1] * x) / weights[2] # 解得决策边界 w0 + w1*x + w2*y = 0
ax.plot(x, y, label="Decision Boundary")
plt.xlabel('X1')
plt.ylabel('X2')
plt.legend()
plt.show()
6.完整代码
import numpy as np
import matplotlib.pyplot as plt
# 加载数据集
def loadDataSet():
dataMat = []
labelMat = []
with open("testSet1.txt") as fr:
for line in fr.readlines():
lineArr = line.strip().split()
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) # 加入偏置项 X0 = 1.0
labelMat.append(int(lineArr[2]))
return dataMat, labelMat
# Sigmoid 函数
def sigmoid(inX):
return 1.0 / (1 + np.exp(-inX))
# 批量梯度下降法
def gradDescent(dataMatIn, classLabels, alpha=0.001, maxCycles=500):
dataMatrix = np.array(dataMatIn)
labelMat = np.array(classLabels).reshape(-1, 1)
m, n = dataMatrix.shape
weights = np.ones((n, 1))
for k in range(maxCycles):
h = sigmoid(np.dot(dataMatrix, weights))
error = h - labelMat
weights = weights - alpha * np.dot(dataMatrix.T, error)
return weights
# 绘图函数:显示分类边界
def plotBestFit(weights):
dataMat, labelMat = loadDataSet()
dataArr = np.array(dataMat)
n = dataArr.shape[0]
xcord1 = []; ycord1 = []
xcord2 = []; ycord2 = []
for i in range(n):
if int(labelMat[i]) == 1:
xcord1.append(dataArr[i, 1])
ycord1.append(dataArr[i, 2])
else:
xcord2.append(dataArr[i, 1])
ycord2.append(dataArr[i, 2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s', label="Class 1")
ax.scatter(xcord2, ycord2, s=30, c='green', label="Class 0")
x = np.arange(-3.0, 3.0, 0.1)
y = (-weights[0] - weights[1] * x) / weights[2]
ax.plot(x, y, label="Decision Boundary")
plt.xlabel('X1')
plt.ylabel('X2')
plt.legend()
plt.show()
# 主程序入口
if __name__ == '__main__':
dataArr, labelMat = loadDataSet()
print("原始数据样例:", dataArr[:3])
print("标签样例:", labelMat[:10])
# 仅使用批量梯度下降
weights = gradDescent(dataArr, labelMat)
print("训练得到的权重参数:\n", weights)
plotBestFit(weights.flatten())
7.运行结果
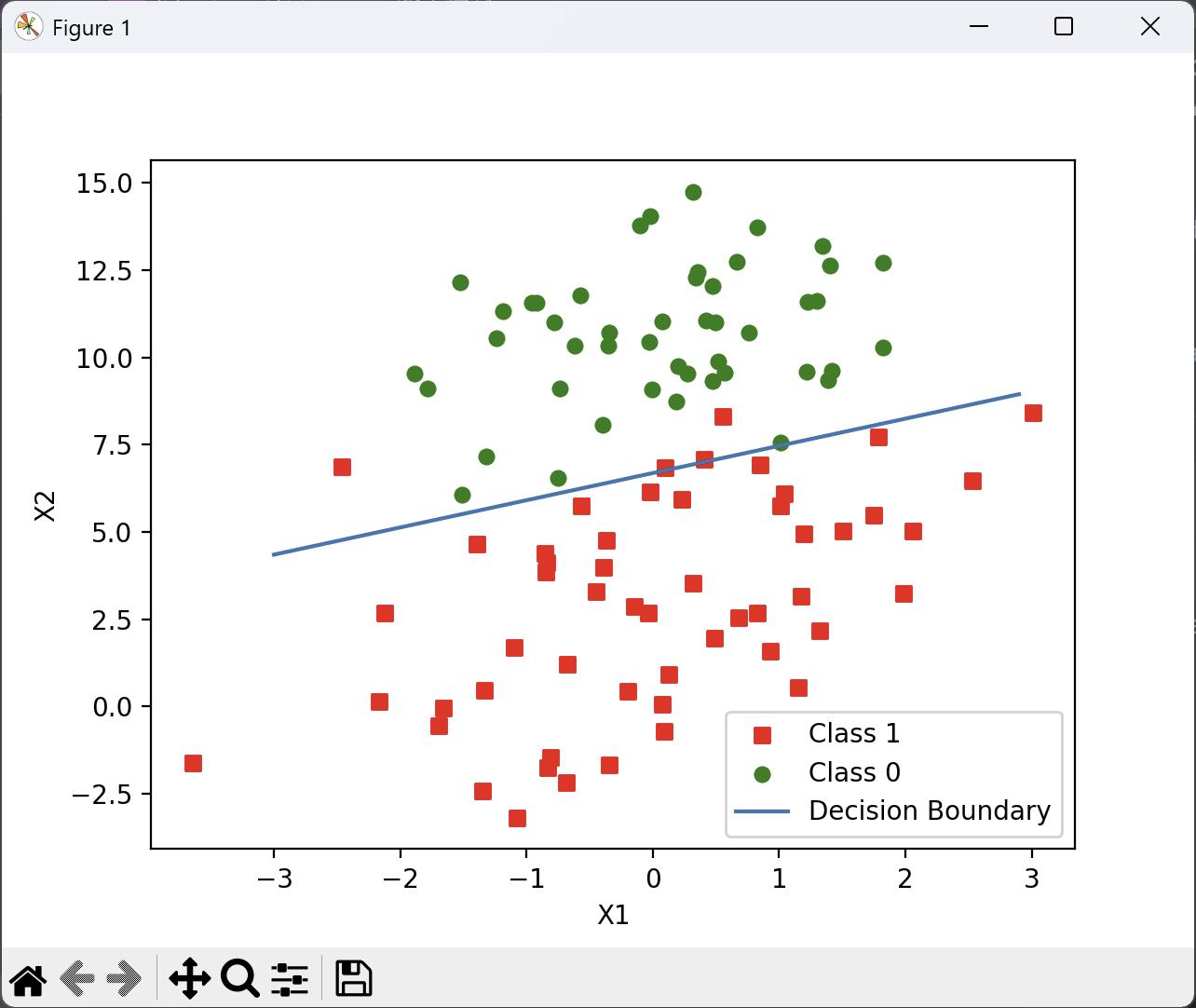

三、感受
通过本次实验,我深入学习了逻辑回归模型的基本原理及其在二分类问题中的应用,重点掌握了如何利用批量梯度下降算法(Batch Gradient Descent)对模型参数进行优化。在代码实现的过程中,我不仅理解了算法的数学推导过程,也更加清晰地认识到每一步的物理意义,比如误差的来源、梯度的作用以及学习率对收敛速度的影响。
实验过程中,我特别关注了梯度下降的实现细节,并通过一个具体的简单样例逐步验证了每一行代码的效果。从数据矩阵的构造到权重向量的更新,再到最终的预测输出,我对逻辑回归模型的工作流程有了更为直观的认识。
此外,实际编码让我意识到数学理论与编程实践之间的差距。虽然公式推导看似简单,但真正用代码表达时,每一步都需要严谨的矩阵运算和数据结构理解。尤其在实现误差计算和权重更新时,通过调试和观察每一次迭代的结果,我对“模型如何逐步拟合数据”有了更深入的体会。
总的来说,这次实验不仅帮助我掌握了逻辑回归的基本训练流程,更让我体会到了机器学习模型背后“由简入繁、由浅入深”的设计逻辑。今后我希望能继续探索更复杂的模型,并通过实际动手实现,不断提升自己将理论落地为代码的能力。























 1258
1258

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








