进制和进制转换

基数和权

为了便于描述，首先引入两个基本概念——基数和权。
基数即某种进制中所使用的数字符号的个数。如十进制采用0~9共10个数符因而它的基数为10；同理，二进制的基数为2。为了表述方便，统一将各种进制称为R进制(R取2、8、10、16)。
权表示某种进制的数中不同位置上数字的单位数值，R进制数第i位的权即为Rⁱ。
​某数位的数值等于该位的系数和权的乘积，因此一个十进制数可以表示成各数位上数值的和。例如，十进制数1234.567可以表示成：(1234.567)₁₀
=1×10³+2×10²+3×10¹+4×10⁰+5×10⁻¹+6×10⁻²+7×10⁻³

进制

进制即进位计数制，它是一种科学的计数方法，以累计和进位的方式进行计数，实现用较少的符号表示较大范围数字的目的。在计算机的设计与使用上常常使用的是十进制、二进制、八进制、十六进制，下面分别加以介绍：

十进制

十进制数中有十个不同的数字符号：0、1、2、3、4、5、6、7、8、9，按照一定顺序排列起来表示数值的大小。十进制的基本运算规则是“逢十进一”。
​任意一个十进制数，如329可表示为(329)₁₀、[329]₁₀或329D。部分情况下表示十进制数后的下标10或字母D地可以省略。

二进制

计算机中使用的是二进制数，二进制数中只有两个数字符号(0和1)，它的基数是2，基本运算规则是“逢二进一”，各数位的权为2的幂。
​

八进制

由于二进制数的书写一般比较长，容易出错，因此为了便于书写，在编写计算机程序时常常用八进制数或十六进制数等价表示二进制数，再由计算机将这些数自动地转换成二进制数。在八进制中，基数为8，它有0、1、2、3、4、5、6、7八个数字符号，八进制的基本运算规则是“逢八进一”，各数位的权为8的幂。

十六进制

十六进制数由0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F十六个数字符号组成，其中的A、B、C、D、E、F相当于十进制数中的10、11、12、13、14、15的值。十六进制数的基数是16，进位方法是“逢十六进一”，各数位的权为16的幂。

进制的转换

二进制、八进制、十六进制转化为十进制

二进制、八进制、十六进制数转换为士进制数的方法可以归纳为：各位按权展开并相加。
​
例：将(5F)₁₆、(123.4)₈、(1010.11)₂转换为十进制
​解：
​(5F)₁₆
=5×16¹+15×16⁰
=80+15
=(95)₁₀

​(123.4)₈
=1×8²+2×8’+3×8⁰+4×8⁻¹
=64+16+3+0.5
=(83.5)₁₀

​(1101.11)₂
=1×2³+1×2²+0×2¹+1×2⁰+1×2⁻¹+1×2⁻²
=8+4+1+0.5+0.25
= (13.75)₁₀

十进制数转换为二进制、八进制、十六进制数

十进制转换为R进制的方法可描述为：将整数部分采用“除R取余法”转换为R进制整数，小数部分采用“乘R取整法”转换放进小数，再将两部分结果合并在一起。
除R取余法：整数部分逐次除以R，将每次得到的余数从后向前读取，则得到R进制数对应的整数部分。​
乘R取整法：小数部分逐次乘以R，取出每次乘积的整数部分，乘到积为0或达到所要求的精度为止。将每次得到的整数从前往后读取，则得到R进制数对应的小数部分。 ​
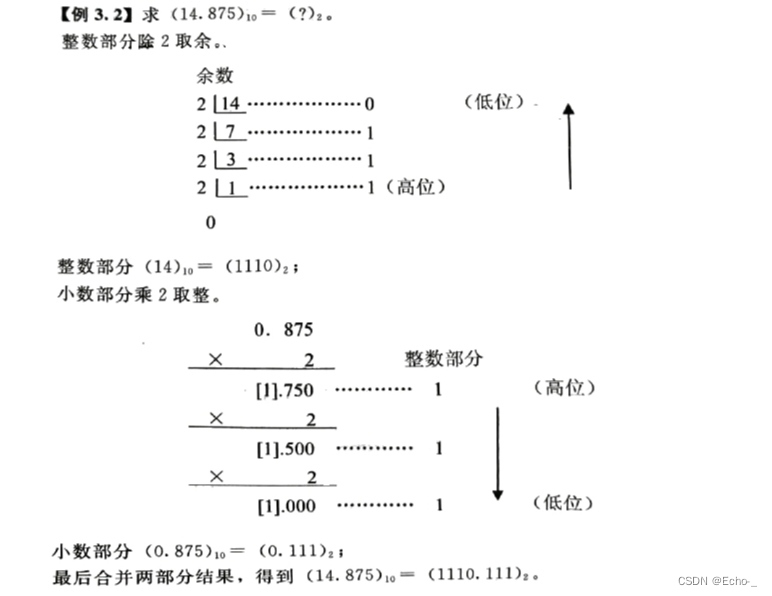十进制数转换成八进制、十六进制的方法，与转换为二进制的方法类似，唯一的变化是除数和乘数由2变成8或16。
​

二进制数和八进制数、十六进制数间的相互转换

因为二进制数的基数是2，八进制数的基数是8，而2³=8，所以3位二进制数与1位八进制数相对应。
二进制数转换为八进制数的方法是：整数部分从低位到高位，每3位为一组，至最高位不足3位时，高位补0；小数部分从高位到低位，每3位为一组，至最低位不足3位时，低位补0，然后将每组二进制数用1位等值的八进制数代替即可。