经典排序算法（插入排序、冒泡排序、选择排序、快速排序、希尔排序、海量数据的外部排序）学习笔记

于 2025-02-17 11:32:03 发布
阅读量1.1k 收藏 7
点赞数 33
分类专栏： 数据结构与算法学习笔记 文章标签： 算法 数据结构
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/2401_82762455/article/details/145678544
版权

只需要记住冒泡排序和快速排序即可，其他记住更好

一、 插入排序思路

插入排序的思路也很简单：假设前面已经有ii节点是有序的，那么就从第i+1i+1个节点开始，插入到前面的ii个节点的合适的位置中。由于第一个元素自身总是有序的，因此从第2个开始，不断插入前面的有序序列，直到全部排列完毕。

假设总共有nn个节点，那么总共需要将n−1n−1个节点插入到有序序列中，而插入节点时需要找到合适的位置，显然这个查找的过程时间复杂度是O(n−i)O(n−i)，因此插入排序的时间复杂度是O(n−1)(n−i)O(n−1)(n−i)，即O(n2)O(n2)

#include <stdio.h>
#include <stdbool.h>

int swap_count = 0;
int comp_count = 0;

void show(int data[], int len)
{
    int i;
    for(i=0; i<len; ++i)
    {
        printf("%d\t", data[i]);
    }
    printf("\n");
}

void insertionSort(int data[], int len)
{
    if(len <= 1)
        return;

    int i, j;
    for(i=1; i<len; i++)
    {
        int tmp = data[i];

        for(j=i-1; j>=0; j--)
        {
            comp_count++;
            if(data[j] < tmp)
            {
                break;
            }
            else
            {
                swap_count++;
                data[j+1] = data[j];
            }
        }
        swap_count++;
        data[j+1] = tmp;
    }
}

int main(int argc, char **argv)
{
    srand(time(NULL));

    int i, data[100];
    for(i=0; i<100; ++i)
    {
        data[i] = rand() % 1000;
    }
    printf("随机序列: ");
    show(data, 100);

    printf("插入排序: ");
    insertionSort(data, 100);
    show(data, 100);

    printf("总共比较次数: %d\n", comp_count);
    printf("总共移动次数: %d\n", swap_count);

    return 0;
}

二、冒泡排序

首先引入两个概念：

  • 顺序：如果两个数据的位置符合排序的需要，则称它们是顺序的。
  • 逆序：如果两个数据的位置不符合排序需要，则称它们是逆序的。

冒泡排序基于这样一种简单的思路：从头到尾让每两个相邻的元素进行比较，顺序就保持位置不变，逆序就交换位置。可以预料，经过一轮比较，序列中具有“极值”的数据，将被挪至序列的末端。

假如序列中有nn个数据，那么在最极端的情况下，只需要经过n−1n−1轮的比较，则一定可以将所有的数据排序完毕。冒泡法排序的时间复杂度是O(n2)O(n2)

#include <stdio.h>

int comp_count = 0; // 数据比较次数
int swap_count = 0; // 数据交换次数

void show(int data[], int len)
{
    int i;
    for(i=0; i<len; ++i)
    {
        printf("%d\t", data[i]);
    }
    printf("\n");
}

void swap(int *a, int *b)
{
    swap_count++;

    int tmp;
    tmp = *a;
    *a = *b;
    *b = tmp;
}

void bubbleSort(int data[], int len)
{
    int k=0;
    while(1)
    {
        bool done = true;

        int i;
        for(i=0; i<len-1-k; i++)
        {
            comp_count++;

            if(data[i] <= data[i+1])
            {
                continue;
            }
        
            swap(&data[i], &data[i+1]);
            done = false;
        }

        if(done)
            break;
        k++;
    }
}

int main(int argc, char **argv)
{
    srand(time(NULL));

    int i, data[100];
    for(i=0; i<100; ++i)
    {
        data[i] = rand() % 1000;
    }
    printf("随机序列: ");
    show(data, 100);

    bubbleSort(data, 100);  // 按升序排列
    printf("冒泡排序: ");
    show(data, 100);

    printf("总共比较次数: %d\n", comp_count);
    printf("总共交换次数: %d\n", swap_count);
    return 0;
}

三、选择排序

选择排序的思路非常简单，就是依次从头到尾挑选合适的元素放到前面。如果总共有nn个节点，那么选择一个合适的节点需要比较nn次，而总共要选择nn次，因此总的时间复杂度是O(n2)O(n2)

下面以无序数组data为例，假设存储的是整型数据，让其从小到大排序，示例代码：

#include <stdio.h>
#include <stdbool.h>

int comp_count = 0; // 数据比较次数
int swap_count = 0; // 数据交换次数

void show(int data[], int len)
{
    int i;
    for(i=0; i<len; ++i)
    {
        printf("%d\t", data[i]);
    }
    printf("\n");
}

void swap(int *a, int *b)
{
    swap_count++;

    int tmp;
    tmp = *a;
    *a = *b;
    *b = tmp;
}

void selectionSort(int data[], int len)
{
    for(int i=0; i<len; i++)
    {
        int min=i;

        for(int j=i+1; j<len; j++)
        {
            comp_count++;
            if(data[j] < data[min])
                min = j;
        }

        swap(&data[i], &data[min]);
    }
}

int main(int argc, char **argv)
{
    srand(time(NULL));

    int i, data[100];
    for(i=0; i<100; ++i)
    {
        int exp = (int)pow(10, rand()%3+3);
        data[i] = rand() % exp;
    }
    printf("随机序列: ");
    show(data, 100);

    selectionSort(data, 100);
    printf("选择排序: ");
    show(data, 100);

    printf("总共比较次数: %d\n", comp_count);
    printf("总共交换次数: %d\n", swap_count);
    return 0;
}

四、快速排序

1.基本思路

快排是一种递归思想的排序算法，先比较其他的排序算法，它需要更多内存空间，但快排的语句频度是最低的，理论上时间效率是最高的。

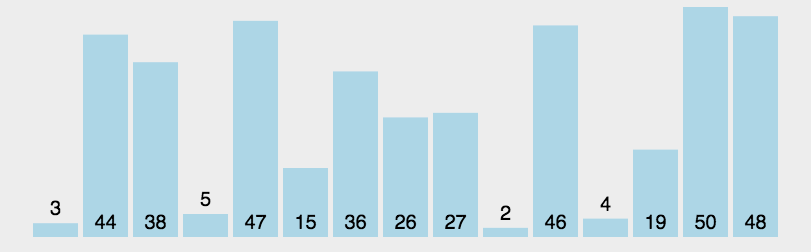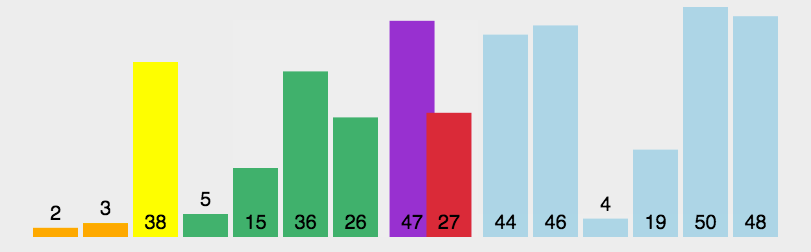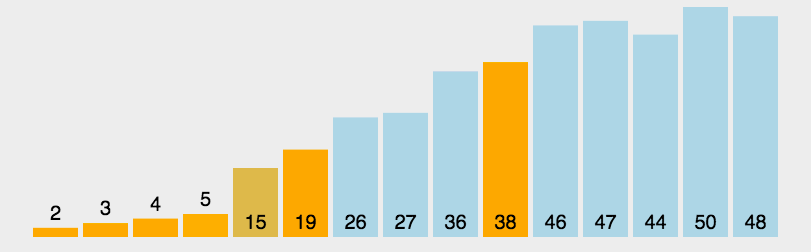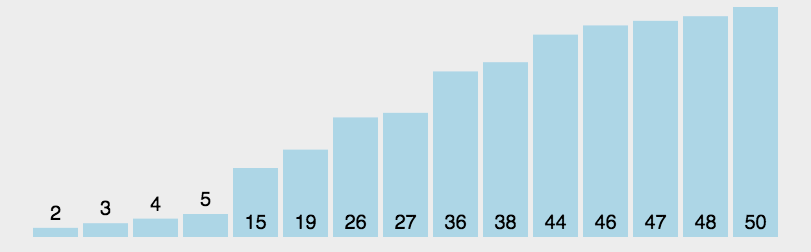
快速排序的基本思路是：在待排序序列中随便选取一个数据，作为所谓“支点”，然后所有其他的数据与之比较，以从小到大排序为例，那么比支点小的统统放在其左边，比支点大的统统放在其右边，全部比完之后，支点将位与两个序列的中间，这叫做一次划分（partition）。

一次划分之后，序列内部也许是无序的，但是序列与支点三者之间，形成了一种基本的有序状态，接下去使用相同的思路，递归地对左右两边的子序列进行排序，直到子序列的长度小于等于1为止。

#include <stdio.h>

int comp_count = 0;
int swap_count = 0;

void show(int data[], int len)
{
    int i;
    for(i=0; i<len; ++i)
    {
        printf("%d\t", data[i]);
    }
    printf("\n");
}

void swap(int *a, int *b)
{
    swap_count++;

    int tmp;
    tmp = *a;
    *a = *b;
    *b = tmp;
}

int partition(int data[], int len)
{
    if(len <= 1)
        return 0;

    int i = 0;
    int j = len-1;
    while(i < j)
    {
        // 从右向左比较，顺序j--，逆序交换
        comp_count++;
        while(data[i]<=data[j] && i<j)
            j--;
        swap(&data[i], &data[j]);

        // 从左向右比较，顺序i++，逆序交换
        comp_count++;
        while(data[i]<=data[j] && i<j)
            i++;
        swap(&data[i], &data[j]);
    }

    return i;
}

void quickSort(int data[], int len)
{
    if(len <= 1)
        return;

    int pivot = partition(data, len);

    quickSort(data, pivot);
    quickSort(data+pivot+1, len-pivot-1);
}

int main(int argc, char **argv)
{
    srand(time(NULL));

    int i, data[100];
    for(i=0; i<100; ++i)
    {
        data[i] = rand() % 1000;
    }
    printf("随机序列: ");
    show(data, 100);

    printf("快速排序: ");
    quickSort(data, 100);
    show(data, 100);

    printf("总共比较次数: %d\n", comp_count);
    printf("总共交换次数: %d\n", swap_count);

    return 0;
}

五、希尔排序

希尔排序是一种改进版的插入排序，普通的插入排序算法中，是从第2个节点开始，依次插入到有序序列中，这种做法虽然“一次成形”，但研究发现时间效率上这么做并不划算，更“划算”的做法是这样的：

不严格一个个插入使之有序，而是拉开插入节点的距离，让它们逐步有序，比如如下图所示，有无无序列：

84、83、88、87、61、50、70、60、80、99

第一遍，先取间隔为（Δ=5Δ=5），即依次对以下5组数据进行排序：

84、83、88、87、61、50、70、60、80、99
84、83、88、87、61、50、70、60、80、99
84、83、88、87、61、50、70、60、80、99
84、83、88、87、61、50、70、60、80、99
84、83、88、87、61、50、70、60、80、99

注意，当对84和50进行排序时，其他的元素就像不存在一样。因此，经过上述间隔为5的一遍排序后，数据如下：

50、83、88、87、61、84、70、60、80、99
50、70、88、87、61、84、83、60、80、99
50、70、60、87、61、84、83、88、80、99
50、70、60、80、61、84、83、88、87、99
50、70、60、80、61、84、83、88、87、99

最终的结果（50、70、60、80、61、84、83、88、87、99）是经过这一遍间隔Δ=5Δ=5的情况下达成的，接下去缩小间隔重复如上过程。例如让间距Δ=3Δ=3：

50、70、60、80、61、84、83、88、87、99
50、70、60、80、61、84、83、88、87、99
50、70、60、80、61、84、83、88、87、99
50、70、60、80、61、84、83、88、87、99

将上述粗体的每一组数据进行排序，得到：

50、70、60、80、61、84、83、88、87、99
50、61、60、80、70、84、83、88、87、99
50、61、60、80、70、84、83、88、87、99
50、61、60、80、70、84、83、88、87、99

最终的结果（50、61、60、80、70、84、83、88、87、99）更加接近完全有序的序列。接下去继续不断减小间隔，最终令Δ=1Δ=1，确保每一个元素都在恰当的位置。动图展示如下：

#include <stdio.h>
#include <math.h>

int comp_count = 0;
int swap_count = 0;

void show(int data[], int len)
{
    int i;
    for(i=0; i<len; ++i)
    {
        printf("%d\t", data[i]);
    }

    printf("\n");
    return;
}

//                    起点    节点个数    间距
void insert_sort(int data[], int len, int delta)
{
    if(len <= 1)
        return;

    for(int i=delta; i<len*delta; i+=delta)
    {
        int j, tmp = data[i];
        for(j=i-delta; j>=0; j-=delta)
        {
            comp_count++;
            if(data[j] < tmp)
                break;

            swap_count++;
            data[j+delta] = data[j];
        }

        data[j+delta] = tmp;
    }
}

void shell_sort(int data[], int len)
{
    if(len <= 1)
        return;

    for(int delta=len/2; delta>0; delta/=2)
    {
        for(int i=0; i<delta; ++i)
        {
            //           起点     节点个数    间距
            insert_sort(data+i, len/delta, delta);
        }
    }
}

int main(void)
{
    // 准备产生一些随机数
    srand(time(NULL));

    int i, data[100];
    for(i=0; i<100; i++)
    {
        int exp = (int)pow(10, rand()%3+3);
        data[i] = rand()%exp;
    }
    printf("随机序列: ");
    show(data, 100);

    printf("希尔排序: ");
    shell_sort(data, 100);
    show(data, 100);

    printf("总共比较次数: %d\n", comp_count);
    printf("总共移动次数: %d\n", swap_count);

    return 0;
}

六、海量数据的外部排序

所谓的外排序，就是指待排序的数据量太大，以至于内存空间无法一次性载入所有的数据，只能借助于外存而进行的排序算法。

从上述定义可以看到，外排序的本质还是内排序，只是多了许多IO操作，需要将部分数据从外存读入内存，排好序后再存储到外存，然后再读取下一部分的数据，以此类推，最后将所有已经排好序的数据全部整合到一个单一的文件中。

比如，用如下代码产生100万个随机数据，并放入一个叫“numbers.txt”的文件中：

#include <sys/stat.h>
#include <sys/types.h>
#include <math.h>
#include <stdio.h>
#include <fcntl.h>

int main(int argc, char **argv)
{
    FILE *fp = fopen("numbers.txt", "w");

    srand(time(NULL));

    int i;
    for(i=0; i<1000*1000; i++)
    {
        fprintf(fp, "%u\n", rand()%((int)pow(10, rand()%8+5)));
    }

    fclose(fp);

    return 0;
}

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

DIY机器人工房

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值