【树表的相关查找算法】-----二叉排序树

1.树表的查找与二叉排序树的相关概念

1.1为什么要用到动态查找表（即几种特殊的树）

1.2二叉排序树的相关概念

1.2.1二叉排序树的递归定义

注意，二叉排序树的严格定义应是
左子树小于根结点，右子树大于根结点

这里的定义是：右子树大于等于根结点，实际上不是最经典的二叉排序树的定义，可根据实际情况灵活选择

1.2.2几个具体实例如下

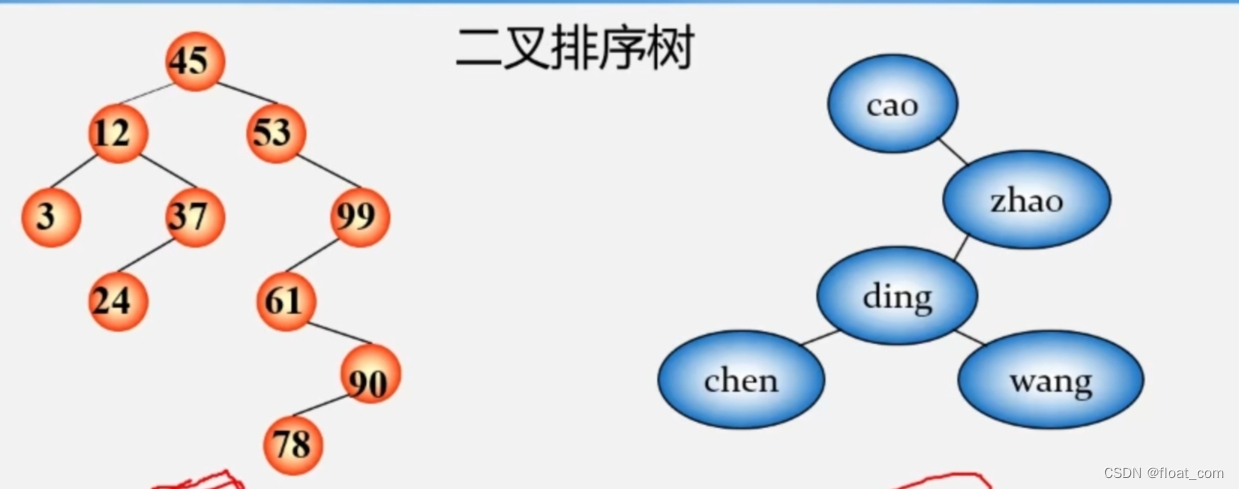
• 如图左边这棵二叉排序树是按照数字大小进行排序的。

（严格按照左子树小于根结点，右子树大于(等于)根结点）

• 同理右边这棵二叉排序树是按照字母的ASCII表大小进行排序的。

两个非二叉排序树的示例如下：

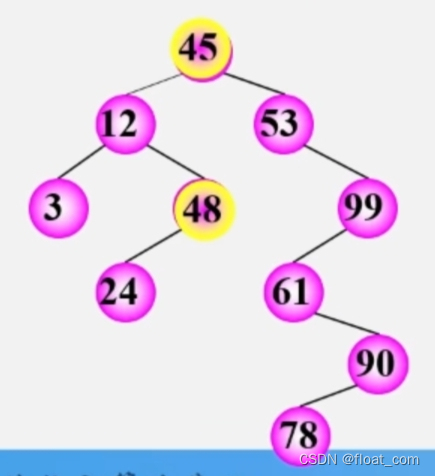
如图，明显我们可以得知结点48大于整棵树的根结点45，根据二叉排序树的定义，结点48应该存储在右子树中，故这是一颗非二叉排序树

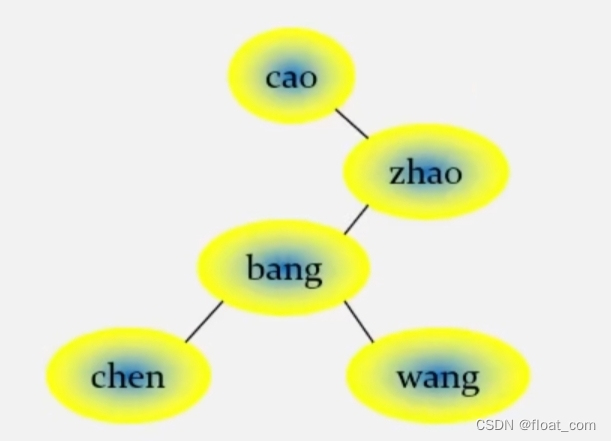
同理，bang中b大于cao中的c，而bang结点应该存储在右子树中，故这是一颗非二叉排序树

1.2.3二叉排序树的性质

比如中序遍历下图这颗二叉排序树：

我们就可以获得一个递增有序序列：

1.2.4二叉排序树的存储结构：

//二叉排序树的结构定义（二叉链表）：

#define KeyType int
//二叉排序树中结点中  关键字 的数据类型

//1.定义结点结构体
typedef struct
{
	KeyType key;//定义关键字域

	//同样可以定义其他数据域
}ElemType;
//ElemType:二叉排序树中每个结点的数据类型


//2.定义二叉链表（与二叉树完全一致）
typedef struct BSTNode
{
	ElemType data;//数据域
	struct BSTNode* lchild, * rchild;//左，右孩子指针
}BSTNode ,*BSTree;
//BSTNode:用来定义二叉排序树的结点类型
//BSTree:用来定义二叉排序树

1.3二叉排序树的基础算法

1.3.1二叉排序树的查找算法（递归定义）

1.3.1.1思路与代码分析

返回值：查找成功返回指向该结点的指针，否则返回NULL
参数：T是二叉排序树的指向根结点的指针，key是要查找的关键字

算法思路：

• （1）递归终止条件：T为空（可能是空树的情况，也可能是没找到待查找结点的情况），或者找到关键字为key的结点，返回该结点指针
  为空时直接返回了NULL，找到相应关键字时返回了对应的地址
• （2）若key小于当前T结点关键字，则递归查找左子树
• （3）若key大于当前T结点关键字，则递归查找右子树

代码实现：

//1.二叉排序树的查找算法：
//返回值：查找成功返回指向该结点的指针，否则返回NULL
//参数：T是二叉排序树的指向根结点的指针，key是要查找的关键字
BSTree  SearchBSTree (BSTree T,KeyType key)
{
	//[1]递归终止条件：（*T）为空（可能是空树的情况，也可能是没找到待查找结点的情况），或者找到关键字为key的结点，返回该结点指针
	if (!T || T->data.key == key)
	{
		return T;
	}
	//[2]若key小于当前T结点关键字，则递归查找左子树
	// （二叉查找树的性质：左子树中所有结点小于根结点，右子树中所有结点大于根结点）
	else if (key < T->data.key)
	{
		return SearchBSTree(T->lchild, key);
	}
	//[3]若key大于当前T结点关键字，则递归查找右子树
	// （二叉查找树的性质：左子树中所有结点小于根结点，右子树中所有结点大于根结点）
	else
	{
		return SearchBSTree(T->rchild, key);
	}
}

实例分析如下：

1.3.1.2算法分析

查找过程分析：

• 回忆：
  
• 二叉排序树上查找某关键字等于给定值的结点过程，其实就是走了一条从根到该结点的路径。

于是我们得到以下两个性质：

比如查找这个35就需要比较4次

二叉排序树的平均查找长度：

根据上述实例，我们发现 平均查找长度和树的高度有关

1.3.2二叉排序树的插入算法 与 生成（递归定义）

1.3.2.1思路与代码分析

参数：参数：T 是指向二叉排序树的根结点指针的 二级指针
注意递归调用时，使用（*T）的地址 即&（*T）

算法思路：

• （1）递归终止条件:若当前根结点为空，则直接建立新结点，作为根结点，并插入数据，初始化左右孩子（指针域置空）
• （2）若当前待插入结点的值大于根结点，递归查找右子树并进行插入
• （3）若当前待插入结点的值小于根结点，递归查找左子树并进行插入
• （4） 若当前待插入结点的值等于根结点，则表示该关键字已经存在，不插入

代码实现：

//2.二叉排序树的插入算法：
//参数：T 是指向二叉排序树的根结点指针的 二级指针
bool InsertBST(BSTree *T, KeyType key)
{
	//[1]若当前根结点为空，则直接建立新结点，作为根结点，并插入数据，初始化左右孩子（指针域置空）
	if (!(*T))
	{
		*T = (BSTNode*)malloc(sizeof(BSTNode));

		if (!(*T))
		{
			printf("内存分配失败！");
			exit(-1);
		}

		(*T)->data.key = key;
		//易错1：注意置空左右孩子的指针域
		(*T)->lchild = NULL;
		(*T)->rchild = NULL;

		//易错2：注意返回条件不能忘记
		return true;
	}
	//[2]若当前待插入结点的值大于根结点，递归查找右子树并进行插入
	else if(key > (*T)->data.key)
	{
		return InsertBST(&(*T)->rchild, key);
	}
	//[3]若当前待插入结点的值小于根结点，递归查找左子树并进行插入
	else if(key < (*T)->data.key)
	{
		return InsertBST(&(*T)->lchild, key);
		//易错：注意传入二级指针：即（*T）的地址
	}
	//[4]若当前待插入结点的值等于根结点，则表示该关键字已经存在，不插入
	else
	{
		return false;
	}
}

1.3.2.2算法分析

生成二叉树的方式------通过插入函数进行操作

• 从空树出发，经过一系列的查找、插入操作之后，可生成一栋二叉排序树。
• 插入的元素一定在叶子结点上
  

生成二叉排序方式的分析

• 一个无序序列可通过构造二叉排序树而变成一个有序序列。
  构造树的过程就是对无序序列进行排序的过程。
• 插入的结点均为叶子结点，故无需移动其他结点。相当于在有序序列上插入记录而无需移动其他记录。

但是要着重注意：


如上图：虽然是同一批关键字序列，但由于插入次序的不同，最终建立的二叉排序树就不同

但是中序遍历两颗树，获得的关键字序列是完全一样的递增有序序列

这里使用了两种不同的插入序列，将同一批关键字序列插入生成两颗二叉排序树，显然这两棵树的形态不同，但其中序遍历的结果是相同的（二叉排序树的性质）

1.4二叉排序树的删除算法

1.4.1删除过程中的注意事项

• （1）从二叉排序树中删除一个结点，不能把以该结点为根的子树都删去，只能删去该结点
• （2）并且还应保证删除后所得的二又树仍然满足二叉排序树的性质不变

由于中序遍历二叉排序树可以得到一个递增有序的序列。那么，在二又排序树中删去一个结点相当于删去有序序列中的一个结点。

删除之后应进行的相关处理：

1.4.2删除操作的具体思路如下：

1.4.2.1 被删除的结点是叶子结点：直接删除该结点，注意其双亲的相应指针域应指向空(NULL)

比如对于下列这颗二叉树进行删除结点20和88的操作：

1.4.2.2 被删除的结点只有左子树或者只有右子树，用其左子树或者右子树替换它(结点替换）------其双亲结点相应的指针域应指向被 删除结点的左子树 或者右子树

比如对于下列这颗二叉树进行删除结点40和80的操作：

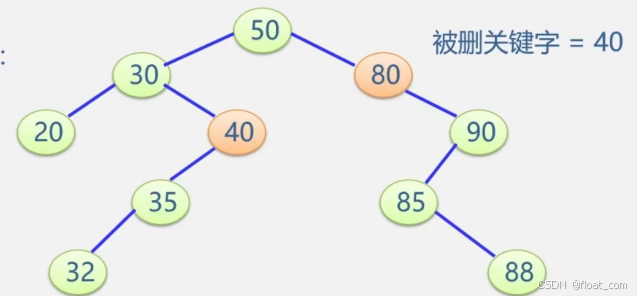
1.4.2.3 被删除的结点既有左子树，也有右子树

方法有两种：

注意这里的删除前驱或者删除后继的操作是递归进行的

比如对于下列这颗二叉树进行删除结点50的操作：
这里使用第一种方法：以中序前驱值替换之

实际上，对于两种方法的使用都有可能会使删除后的二叉排序树高度增高，这可能会造成后续查找时的复杂度变大

1.4.3相关代码与算法思路总结

1.4.3.1中序后继法：

1.4.3.1.1思路汇总：

• （1）递归终止条件：

如果当前树节点为空 (*T 为 NULL)，则返回 false，表示没有找到待删除的关键字或树本身为空。

• （2）递归寻找待删除节点：

• （2.1）如果待删除的关键字 key 大于当前节点的关键字，则递归到当前节点的右子树进行删除。

• （2.2）如果待删除的关键字 key 小于当前节点的关键字，则递归到当前节点的左子树进行删除。

• （3）处理找到的待删除节点：

如果当前节点的关键字等于待删除的关键字，进入处理删除的逻辑

• （3.1）情况 1：无左右孩子（叶子节点）：

释放该节点的内存，并将该节点指针置为空 (NULL)。

• （3.2）情况 2：只有左孩子：

使用左孩子替代待删除节点，释放待删除节点的内存。

• （3.3）情况 3：只有右孩子：

使用右孩子替代待删除节点，释放待删除节点的内存。

• （3.4）核心情况 4：有左右孩子：

使用中序后继节点（即右子树中的最小节点）替代待删除节点。 具体步骤：
【1】从当前节点的右子树开始，寻找最小的节点（即中序后继节点），该节点位于其左子树的最右下角。
【2】将当前节点的数据替换为中序后继节点的数据。
【3】递归删除中序后继节点，注意传入的是右孩子指针的地址，以避免删除已经替换的当前节点。

参数分别为 指向当前二叉排序树的地址的二级指针 和 待删除关键字

//4.1二叉排序树的删除算法：
//(这里使用中序后继法)

bool DeleteBST(BSTree* T, KeyType key)
{
	//[1]递归终止条件：（*T）为空（空树的情况 或者 没找到关键字），返回false
	if (!(*T))
	{
		return false;
	}

	//[2]递归寻找待删除的结点

	//<2.1>若key大于当前结点的关键字，则递归到右子树删除
	else if (key > (*T)->data.key)
	{
		return DeleteBST(&(*T)->rchild, key);
	}

	//<2.2>若key小于当前结点的关键字，则递归到左子树删除
	else if (key < (*T)->data.key)
	{
		return DeleteBST(&(*T)->lchild, key);
	}

	//[3]找到了待删除结点，处理删除的三种情况
	else
	{
		//<3.1> 若待删除结点无左右孩子（叶子结点），直接删除
		// 具体操作：(释放该结点的内存 并 将该结点置空)
		if ((*T)->lchild==NULL&& (*T)->rchild == NULL)
		{
			free(*T);//释放该结点的内存
			(*T) = NULL;// 将该结点置空
			return true;
		}

		//<3.2>若待删除结点只有左孩子，左孩子代替该结点
		//具体操作：定义临时指针指向待删除结点，替换待删除结点，释放临时指针指向的待删除结点的内存
		else if ((*T)->lchild != NULL && (*T)->rchild == NULL)
		{

			BSTNode* DeleteNode = (*T);//定义临时指针指向待删除结点

			(*T) = (*T)->lchild;//用左孩子代替该结点

			free(DeleteNode);//释放该结点内存

			return true;
		}

		//<3.3>若待删除结点只有右孩子，右孩子代替该结点
		//具体操作：定义临时指针指向待删除结点，替换待删除结点，释放临时指针指向的待删除结点的内存
		else if ((*T)->lchild == NULL && (*T)->rchild != NULL)
		{

			BSTNode * DeleteNode = (*T); //定义临时指针指向待删除结点

			(*T) = (*T)->rchild;//用右孩子代替该结点

			free(DeleteNode);//释放该结点内存

			return true;
		}
		
		//<3.4>若待删除结点有左右孩子，选择中序后继（右子树的最小结点）替代
		else if ((*T)->lchild != NULL && (*T)->rchild != NULL)
		{
			//<3.4.1>寻找中序后继结点（右子树的最小结点）,用新的临时指针指向这个结点
			//注意：这里必须从(*T)->rchild开始查找，因为中序后继首先要比当前结点要大
			BSTNode* MinNode = (*T)->rchild;


			//这里使用了二叉排序树的性质，右子树的最小结点在 其左子树的最后一个左孩子的位置
			while (MinNode->lchild != NULL)
			{
				MinNode = MinNode->lchild;
			}


			//<3.4.2>用中序后继结点（右子树的最小结点）替代当前结点(只交换内容)
			(*T)->data = MinNode->data;


			//<3.4.3>递归删除中序后继结点
			//注意1：传入的是右孩子指针的地址；
			//因为删除的是右子树最小结点,同时避免了将已经替换了的当前结点误删
			return DeleteBST(&((*T)->rchild), MinNode->data.key);
		}
	}
}

1.4.3.1.2注意事项：

对于待删除结点有左右孩子这种情况

• (1) 不能从 *T（当前待删除结点）开始查找中序后继的原因是 ：
  
• （2）递归删除中序后继结点时，注意传入的两个参数
  分别是：右孩子指针的地址 和中序后继结点的关键字

1.4.3.2中序前驱法：

1.4.3.2.1思路汇总：

与中序后继法非常相似，只有待删除结点有左右孩子这种情况的处理与其不同，其余操作与中序后继法完全一致

• （1）递归终止条件：

如果当前树节点为空 (*T 为 NULL)，则返回 false，表示没有找到待删除的关键字或树本身为空。

• （2）递归寻找待删除节点：

• （2.1）如果待删除的关键字 key 大于当前节点的关键字，则递归到当前节点的右子树进行删除。

• （2.2）如果待删除的关键字 key 小于当前节点的关键字，则递归到当前节点的左子树进行删除。

• （3）处理找到的待删除节点：

如果当前节点的关键字等于待删除的关键字，进入处理删除的逻辑

• （3.1）情况 1：无左右孩子（叶子节点）：

释放该节点的内存，并将该节点指针置为空 (NULL)。

• （3.2）情况 2：只有左孩子：

使用左孩子替代待删除节点，释放待删除节点的内存。

• （3.3）情况 3：只有右孩子：

使用右孩子替代待删除节点，释放待删除节点的内存。

• （3.4）核心情况 4：有左右孩子：

使用中序前驱节点（即左子树中的最大节点）替代待删除节点。 具体步骤：
【1】从当前节点的左子树开始，寻找最大的节点（即中序前驱节点），该节点位于其左子树的最右下角。
【2】将当前节点的数据替换为中序前驱节点的数据。
【3】递归删除中序前驱节点，注意传入的是左孩子指针的地址，以避免删除已经替换的当前节点。

//4.2二叉排序树的删除算法：
//(这里使用中序前驱法)
//这里与中序后继法的唯一区别就是 对 待删除结点为有左右孩子结点的情况，其他部分与中序后继法完全一致
bool DeleteBST1(BSTree* T, KeyType key)
{
	//[1]递归终止条件：（*T）为空（空树的情况 或者 没找到关键字），返回false
	if (!(*T))
	{
		return false;
	}

	//[2]递归寻找待删除的结点

	//<2.1>若key大于当前结点的关键字，则递归到右子树删除
	else if (key > (*T)->data.key)
	{
		return DeleteBST(&(*T)->rchild, key);
	}

	//<2.2>若key小于当前结点的关键字，则递归到左子树删除
	else if (key < (*T)->data.key)
	{
		return DeleteBST(&(*T)->lchild, key);
	}

	//[3]找到了待删除结点，处理删除的三种情况
	else
	{
		//<3.1> 若待删除结点无左右孩子（叶子结点），直接删除
		// 具体操作：(释放该结点的内存 并 将该结点置空)
		if ((*T)->lchild == NULL && (*T)->rchild == NULL)
		{
			free(*T);//释放该结点的内存
			(*T) = NULL;// 将该结点置空
			return true;
		}

		//<3.2>若待删除结点只有左孩子，左孩子代替该结点
		//具体操作：定义临时指针指向待删除结点，替换待删除结点，释放临时指针指向的待删除结点的内存
		else if ((*T)->lchild != NULL && (*T)->rchild == NULL)
		{

			BSTNode* DeleteNode = (*T);//定义临时指针指向待删除结点

			(*T) = (*T)->lchild;//用左孩子代替该结点

			free(DeleteNode);//释放该结点内存

			return true;
		}

		//<3.3>若待删除结点只有右孩子，右孩子代替该结点
		//具体操作：定义临时指针指向待删除结点，替换待删除结点，释放临时指针指向的待删除结点的内存
		else if ((*T)->lchild == NULL && (*T)->rchild != NULL)
		{

			BSTNode* DeleteNode = (*T); //定义临时指针指向待删除结点

			(*T) = (*T)->rchild;//用右孩子代替该结点

			free(DeleteNode);//释放该结点内存

			return true;
		}


		//<3.4>若待删除结点有左右孩子，选择中序前驱（左子树的最大结点）替代
		else if ((*T)->lchild != NULL && (*T)->rchild != NULL)
		{
			//<3.4.1>寻找中序前驱结点（右子树的最小结点）,用新的临时指针指向这个结点
			//注意：这里必须从(*T)->lchild开始查找，因为中序后前驱首先要比当前结点要小
			BSTNode* MaxNode = (*T)->lchild;


			//这里使用了二叉排序树的性质，左子树的最大结点在 其左子树的最后一个右孩子的位置
			while (MaxNode->rchild != NULL)
			{
				MaxNode = MaxNode->rchild;
			}


			//<3.4.2>用中序前驱结点（左子树的最大结点）替代当前结点(只交换内容)
			(*T)->data = MaxNode->data;


			//<3.4.3>递归删除中序前驱结点
			//注意1：传入的是左孩子指针的地址；
			//因为删除的是左子树最小结点,同时避免了将已经替换了的当前结点误删
			return DeleteBST(&((*T)->lchild), MaxNode->data.key);
		}
	}
}

1.4.4删除操作情况汇总：

1.5整体操作代码一览：

#define _CRT_SECURE_NO_WARNINGS 1
//二叉排序树的相关操作
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>

//二叉排序树的结构定义（二叉链表）：

#define KeyType int
//二叉排序树中结点中  关键字 的数据类型

//1.定义结点结构体（实际上就是数据域）
typedef struct
{
	KeyType key;//定义关键字域

	//同样可以定义其他数据域
}ElemType;
//ElemType:二叉排序树中每个结点的数据类型


//2.定义二叉链表（与二叉树完全一致）
typedef struct BSTNode
{
	ElemType data;//数据域
	struct BSTNode* lchild, * rchild;//左，右孩子指针
}BSTNode ,*BSTree;
//BSTNode:用来定义二叉排序树的结点类型
//BSTree:用来定义二叉排序树



//1.二叉排序树的查找算法：
//返回值：查找成功返回指向该结点的指针，否则返回NULL
//参数：T是二叉排序树的指向根结点的指针，key是要查找的关键字
BSTree  SearchBSTree (BSTree T,KeyType key)
{
	//[1]递归终止条件：（*T）为空（可能是空树的情况，也可能是没找到待查找结点的情况），或者找到关键字为key的结点，返回该结点指针
	if (!T || T->data.key == key)
	{
		return T;
	}
	//[2]若key小于当前T结点关键字，则递归查找左子树
	// （二叉查找树的性质：左子树中所有结点小于根结点，右子树中所有结点大于根结点）
	else if (key < T->data.key)
	{
		return SearchBSTree(T->lchild, key);
	}
	//[3]若key大于当前T结点关键字，则递归查找右子树
	// （二叉查找树的性质：左子树中所有结点小于根结点，右子树中所有结点大于根结点）
	else
	{
		return SearchBSTree(T->rchild, key);
	}
}


//2.二叉排序树的插入算法：
//参数：T 是指向二叉排序树的根结点指针的 二级指针
bool InsertBST(BSTree *T, KeyType key)
{
	//[1]若当前根结点为空，则直接建立新结点，作为根结点，并插入数据，初始化左右孩子（指针域置空）
	if (!(*T))
	{
		*T = (BSTNode*)malloc(sizeof(BSTNode));

		if (!(*T))
		{
			printf("内存分配失败！");
			exit(-1);
		}

		(*T)->data.key = key;
		//易错1：注意置空左右孩子的指针域
		(*T)->lchild = NULL;
		(*T)->rchild = NULL;

		//易错2：注意返回条件不能忘记
		return true;
	}
	//[2]若当前待插入结点的值大于根结点，递归查找右子树并进行插入
	else if(key > (*T)->data.key)
	{
		return InsertBST(&(*T)->rchild, key);
	}
	//[3]若当前待插入结点的值小于根结点，递归查找左子树并进行插入
	else if(key < (*T)->data.key)
	{
		return InsertBST(&(*T)->lchild, key);
		//易错：注意传入二级指针：即（*T）的地址
	}
	//[4]若当前待插入结点的值等于根结点，则表示该关键字已经存在，不插入
	else
	{
		return false;
	}
}



//3.二叉排序树的中序遍历：（复习）
//由于二叉排序树的性质：中序遍历二叉排序树，能够获得一个递增有序序列
bool PrintBSTree(BSTree T)
{
	//[1] 返回条件：子树为空，则返回true;
	if (!T)
	{
		return true;
	}

	//[2]递归遍历左子树
	PrintBSTree(T->lchild);

	//[3]访问根结点
	printf("%d ", T->data.key);

	//[4]递归遍历右子树
	PrintBSTree(T->rchild);

}

//4.1二叉排序树的删除算法：
//(这里使用中序后继法)

bool DeleteBST(BSTree* T, KeyType key)
{
	//[1]递归终止条件：（*T）为空（空树的情况 或者 没找到关键字），返回false
	if (!(*T))
	{
		return false;
	}

	//[2]递归寻找待删除的结点

	//<2.1>若key大于当前结点的关键字，则递归到右子树删除
	else if (key > (*T)->data.key)
	{
		return DeleteBST(&(*T)->rchild, key);
	}

	//<2.2>若key小于当前结点的关键字，则递归到左子树删除
	else if (key < (*T)->data.key)
	{
		return DeleteBST(&(*T)->lchild, key);
	}

	//[3]找到了待删除结点，处理删除的三种情况
	else
	{
		//<3.1> 若待删除结点无左右孩子（叶子结点），直接删除
		// 具体操作：(释放该结点的内存 并 将该结点置空)
		if ((*T)->lchild==NULL&& (*T)->rchild == NULL)
		{
			free(*T);//释放该结点的内存
			(*T) = NULL;// 将该结点置空
			return true;
		}

		//<3.2>若待删除结点只有左孩子，左孩子代替该结点
		//具体操作：定义临时指针指向待删除结点，替换待删除结点，释放临时指针指向的待删除结点的内存
		else if ((*T)->lchild != NULL && (*T)->rchild == NULL)
		{

			BSTNode* DeleteNode = (*T);//定义临时指针指向待删除结点

			(*T) = (*T)->lchild;//用左孩子代替该结点

			free(DeleteNode);//释放该结点内存

			return true;
		}

		//<3.3>若待删除结点只有右孩子，右孩子代替该结点
		//具体操作：定义临时指针指向待删除结点，替换待删除结点，释放临时指针指向的待删除结点的内存
		else if ((*T)->lchild == NULL && (*T)->rchild != NULL)
		{

			BSTNode * DeleteNode = (*T); //定义临时指针指向待删除结点

			(*T) = (*T)->rchild;//用右孩子代替该结点

			free(DeleteNode);//释放该结点内存

			return true;
		}
		
		//<3.4>若待删除结点有左右孩子，选择中序后继（右子树的最小结点）替代
		else if ((*T)->lchild != NULL && (*T)->rchild != NULL)
		{
			//<3.4.1>寻找中序后继结点（右子树的最小结点）,用新的临时指针指向这个结点
			//注意：这里必须从(*T)->rchild开始查找，因为中序后继首先要比当前结点要大
			BSTNode* MinNode = (*T)->rchild;


			//这里使用了二叉排序树的性质，右子树的最小结点在 其左子树的最后一个左孩子的位置
			while (MinNode->lchild != NULL)
			{
				MinNode = MinNode->lchild;
			}


			//<3.4.2>用中序后继结点（右子树的最小结点）替代当前结点(只交换内容)
			(*T)->data = MinNode->data;


			//<3.4.3>递归删除中序后继结点
			//注意1：传入的是右孩子指针的地址；
			//因为删除的是右子树最小结点,同时避免了将已经替换了的当前结点误删
			return DeleteBST(&((*T)->rchild), MinNode->data.key);
		}
	}
}

//4.2二叉排序树的删除算法：
//(这里使用中序前驱法)
//这里与中序后继法的唯一区别就是 对 待删除结点为有左右孩子结点的情况，其他部分与中序后继法完全一致
bool DeleteBST1(BSTree* T, KeyType key)
{
	//[1]递归终止条件：（*T）为空（空树的情况 或者 没找到关键字），返回false
	if (!(*T))
	{
		return false;
	}

	//[2]递归寻找待删除的结点

	//<2.1>若key大于当前结点的关键字，则递归到右子树删除
	else if (key > (*T)->data.key)
	{
		return DeleteBST(&(*T)->rchild, key);
	}

	//<2.2>若key小于当前结点的关键字，则递归到左子树删除
	else if (key < (*T)->data.key)
	{
		return DeleteBST(&(*T)->lchild, key);
	}

	//[3]找到了待删除结点，处理删除的三种情况
	else
	{
		//<3.1> 若待删除结点无左右孩子（叶子结点），直接删除
		// 具体操作：(释放该结点的内存 并 将该结点置空)
		if ((*T)->lchild == NULL && (*T)->rchild == NULL)
		{
			free(*T);//释放该结点的内存
			(*T) = NULL;// 将该结点置空
			return true;
		}

		//<3.2>若待删除结点只有左孩子，左孩子代替该结点
		//具体操作：定义临时指针指向待删除结点，替换待删除结点，释放临时指针指向的待删除结点的内存
		else if ((*T)->lchild != NULL && (*T)->rchild == NULL)
		{

			BSTNode* DeleteNode = (*T);//定义临时指针指向待删除结点

			(*T) = (*T)->lchild;//用左孩子代替该结点

			free(DeleteNode);//释放该结点内存

			return true;
		}

		//<3.3>若待删除结点只有右孩子，右孩子代替该结点
		//具体操作：定义临时指针指向待删除结点，替换待删除结点，释放临时指针指向的待删除结点的内存
		else if ((*T)->lchild == NULL && (*T)->rchild != NULL)
		{

			BSTNode* DeleteNode = (*T); //定义临时指针指向待删除结点

			(*T) = (*T)->rchild;//用右孩子代替该结点

			free(DeleteNode);//释放该结点内存

			return true;
		}


		//<3.4>若待删除结点有左右孩子，选择中序前驱（左子树的最大结点）替代
		else if ((*T)->lchild != NULL && (*T)->rchild != NULL)
		{
			//<3.4.1>寻找中序前驱结点（右子树的最小结点）,用新的临时指针指向这个结点
			//注意：这里必须从(*T)->lchild开始查找，因为中序后前驱首先要比当前结点要小
			BSTNode* MaxNode = (*T)->lchild;


			//这里使用了二叉排序树的性质，左子树的最大结点在 其左子树的最后一个右孩子的位置
			while (MaxNode->rchild != NULL)
			{
				MaxNode = MaxNode->rchild;
			}


			//<3.4.2>用中序前驱结点（左子树的最大结点）替代当前结点(只交换内容)
			(*T)->data = MaxNode->data;


			//<3.4.3>递归删除中序前驱结点
			//注意1：传入的是左孩子指针的地址；
			//因为删除的是左子树最小结点,同时避免了将已经替换了的当前结点误删
			return DeleteBST(&((*T)->lchild), MaxNode->data.key);
		}
	}
}




int main()
{
	//注意在主函数中创建二叉排序树时，可以使用插入算法进行创建
	//易错：但是要注意首先将T置空（NULL）以便插入算法进行时能正确判断空树
	BSTree T=NULL;

	//按照：3 12 24 37 45 53 61 78 90 100
	//建立一颗二叉排序树，应该只含有右子树，（因为创建序列为升序）
	InsertBST(&T, 3);
	InsertBST(&T, 12);
	InsertBST(&T, 24);
	InsertBST(&T, 37);
	InsertBST(&T, 45);
	InsertBST(&T, 53);
	InsertBST(&T, 61);
	InsertBST(&T, 78);
	InsertBST(&T, 90);
	InsertBST(&T, 100);
	

	printf("T:");
	PrintBSTree(T);



	printf("\n");

	BSTree T1 = NULL;

	//使用不同的插入序列，但相同的关键字序列，生成一颗二叉排序树并中序遍历
	InsertBST(&T1, 100);
	InsertBST(&T1, 3);
	InsertBST(&T1, 37);
	InsertBST(&T1, 24);
	InsertBST(&T1, 45);
	InsertBST(&T1, 53);
	InsertBST(&T1, 61);
	InsertBST(&T1, 78);
	InsertBST(&T1, 90);
	InsertBST(&T1, 12);

	printf("T1:");
	PrintBSTree(T1);

	printf("\n\n");


	//删除测试：

	//中序后继法删除结点测试
	BSTree T3 = NULL; // 初始化为空树

	// 插入多个结点
	InsertBST(&T3, 50);
	InsertBST(&T3, 30);
	InsertBST(&T3, 20);
	InsertBST(&T3, 40);
	InsertBST(&T3, 70);
	InsertBST(&T3, 60);
	InsertBST(&T3, 80);

	printf("T3:");
	PrintBSTree(T3);

	printf("\n");


	DeleteBST(&T3, 20);  // 删除叶子结点

	printf("T3:");
	PrintBSTree(T3);

	printf("\n");

	DeleteBST(&T3, 30);  // 删除只有一个孩子的结点

	printf("T3:");
	PrintBSTree(T3);

	printf("\n");


	DeleteBST(&T3, 50);  // 删除有两个孩子的结点

	printf("T3:");
	PrintBSTree(T3);

	printf("\n");

	printf("\n\n");
	//中序前驱法删除结点测试
	BSTree T4 = NULL; // 初始化为空树

	// 插入多个结点
	InsertBST(&T4, 50);
	InsertBST(&T4, 30);
	InsertBST(&T4, 20);
	InsertBST(&T4, 40);
	InsertBST(&T4, 70);
	InsertBST(&T4, 60);
	InsertBST(&T4, 80);

	printf("T4:");
	PrintBSTree(T4);

	printf("\n");


	DeleteBST(&T4, 20);  // 删除叶子结点

	printf("T4:");
	PrintBSTree(T4);

	printf("\n");

	DeleteBST(&T4, 30);  // 删除只有一个孩子的结点

	printf("T4:");
	PrintBSTree(T4);

	printf("\n");


	DeleteBST(&T4, 50);  // 删除有两个孩子的结点

	printf("T4:");
	PrintBSTree(T4);

	printf("\n");

	return 0;
}

注意这里两个删除算法可能最终留下的二叉排序树结构是不一样的，
只不过中序遍历的结果是完全相同的（二叉排序树的性质）