图像识别技术与应用（三）

感知机

        应用

                与门

                与非门

                或门

                异或门

        局限性

多层感知机

---------------------------------------------------------------------------------------------------------------------------------

感知机

定义与基本原理

感知机由美国学者弗兰克·罗森布拉特在1957年提出，是神经网络和机器学习领域的基础模型。它模拟生物神经元对信息的处理方式，接收多个输入信号，进行加权求和并与阈值比较，输出0或1表示不同类别。

结构与组成

输入层：接收外界输入的特征向量，每个输入节点对应一个特征。

权重：每个输入连接到神经元都有一个权重，代表该输入对输出的影响程度。

求和单元：对所有加权输入求和。

激活函数：通常使用阶跃函数，当求和结果大于阈值时输出1，否则输出0。

数学表达式

感知机的输出可表示为：y = f(\sum_{i = 1}^{n}w_ix_i - \theta)，其中x_i是输入，w_i是权重，\theta是阈值，f是激活函数。

学习算法

感知机学习算法旨在调整权重以最小化分类错误。采用梯度下降法，根据预测错误更新权重，公式为w_{i}^{new}=w_{i}^{old}+\Delta w_i，\Delta w_i=\eta(y - \hat{y})x_i，\eta是学习率，y是真实标签，\hat{y}是预测标签。

应用

简单分类任务：如判断图像中的数字是奇数还是偶数、文本是正面情感还是负面情感等。

逻辑运算实现：可以实现与、或、非等基本逻辑运算。

与门

逻辑功能：当且仅当两个输入都为1时，输出才为1，否则输出为0。

与非门

逻辑功能：是与门的取反，当两个输入都为1时，输出为0，否则输出为1。

或门

逻辑功能：只要两个输入中有一个为1，输出就为1，只有当两个输入都为0时，输出才为0。

异或门

逻辑功能：两个输入不同时输出为1，相同时输出为0。

局限性

只能处理线性可分问题，对于异或等线性不可分问题无法正确分类。只能表示由一条直线分割的空间。

多层感知机

定义

多层感知机（Multilayer Perceptron，MLP）是在感知机基础上发展而来的一种神经网络。

结构

输入层：接收原始输入数据，每个节点对应一个特征，将数据传递给下一层。

隐藏层：位于输入层和输出层之间，可包含一层或多层。每层由多个神经元组成，神经元通过非线性激活函数对输入进行处理，将处理后的信息传递到下一层，不同隐藏层的神经元可学习到数据不同层次的特征。

输出层：根据任务类型输出结果，如在分类任务中输出属于不同类别的概率，在回归任务中输出连续的数值。

工作原理

前向传播：输入数据从输入层进入，依次经过各隐藏层的计算和处理，最终在输出层得到预测结果。在每一层中，神经元将上一层的输出作为输入，进行加权求和并加上偏置项，再通过激活函数得到该神经元的输出。

反向传播：计算输出结果与真实标签之间的误差，然后将误差从输出层反向传播到输入层，根据误差来调整各层神经元的权重和偏置，以减小误差。通过不断重复前向传播和反向传播过程，使模型逐渐收敛到一个较优的参数状态。

激活函数

激活函数：刚才登场的h（x）函数会将输入信号的总和转换为输出信号，这种函数一般称为激活函数（activation function）。

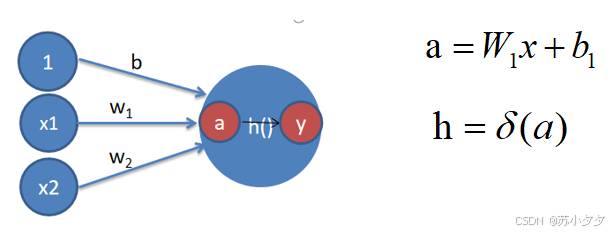
激活函数在神经元中非常重要的。为了增强网络的表示能力和学习能力，激活函数需要具备以下几点性质：

（1） 连续并可导（允许少数点上不可导）的非线性函数。

（2） 激活函数及其导函数要尽可能的简单，有利于提高网络计算效率。

（3） 激活函数的导函数的值域要在一个合适的区间内，不能太大也不能太小，否则会影响训练的效率和稳定性。

阶跃函数：以0为界，一旦输入超过0，就切换输出1；否则输出0。

Sigmoid函数（挤压函数）：将输入映射到(0,1)区间，可将输出解释为概率，但存在梯度消失问题。

ReLU函数（线性修正函数）：计算简单，能有效缓解梯度消失问题，当输入大于0时输出为输入本身，否则为0，是目前常用的激活函数。

Tanh函数（双曲正切）：将输入映射到(-1,1)区间，与Sigmoid函数类似，但中心在0点，收敛速度通常比Sigmoid函数快。

多分类

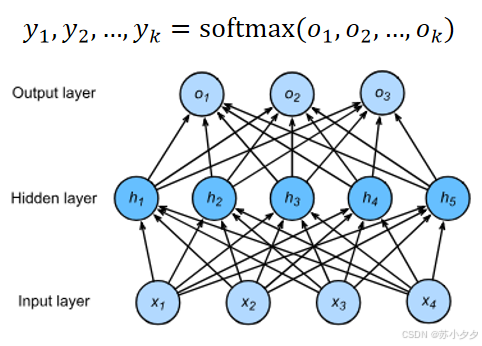
多个隐藏层多分类

总结

多层感知机使用隐藏层和激活函数来得到非线性模型

常用激活函数是Sigmoid，Tanh，RELU

使用Softmax来处理多分类

超参数为隐藏层数和各个隐藏层大小

应用

图像识别：识别图像中的物体、进行图像分类等。

语音识别：将语音信号转换为文字或进行语音指令识别。

自然语言处理：文本分类、情感分析、机器翻译等。

预测与回归：对股票价格、天气等连续数据进行预测。

学习过程和本质

过程：多层感知机使用隐藏层和激活函数来得到非线性模型 常用激活函数是Sigmoid，Tanh，RELU 使用Softmax来处理多分类 超参数为隐藏层数和各个隐藏层大小

本质：对可变权值的动态调整

训练误差和泛化误差

训练误差--模型在训练数据集上的误差

定义

也叫经验误差，是模型在训练数据集上的误差，即模型预测结果与训练数据真实标签之间的差异，反映了模型对训练数据的拟合程度。

例子

用线性回归模型预测房价，训练集包含100个房屋样本的面积和价格数据，模型训练后对这100个样本的预测价格与真实价格的平均差值为5万元，这5万元就是训练误差。

泛化误差--模型在新数据集上的误差

定义

指模型在未见过的新数据（测试集或实际应用中的数据）上的误差，体现了模型对未知数据的预测能力和通用性。

例子

上述房价预测模型训练好后，用它去预测另外50个不在训练集中的房屋价格，预测价格与真实价格的平均差值为8万元，这8万元就是泛化误差。一般来说，模型的目标是在降低训练误差的同时，使泛化误差也尽可能小，以保证模型在实际应用中的有效性。

情况

理想情况下，模型在训练集和新数据上都表现良好，即训练误差和泛化误差都低。但实际中，若模型过于复杂，可能会过度拟合训练数据，导致训练误差低而泛化误差高；若模型过于简单，可能训练误差和泛化误差都高。

验证

K-折交叉验证

将训练数据划分为 K 个部分 对于 i = 1，...，K 使用第 i 部分作为验证集，其余部分用于训练 报告 K 个部分在验证时的平均误差

常见 K 值选择：K=5或10

过拟合和欠拟合

模型复杂度的影响

多种因素很重要： 样本数量 每个样本中的特征数量 时间、空间结构 多样性

---------------------------------------------------------------------------------------------------------------------------------

（所有数据信息，均来自于网络）