day2笔记

1.算法与算法分析1

算法：求解问题和步骤的一种描述，指令的有限序列

算法描述：

• 自然语言：中文
• 流程图：Ns流程图
• 伪代码：类C语言
• 程序代码：C

算法特性：

​ 有穷性、确定性、可行性、输入、输出

算法设计的要求：

​ 正确性、可读性、健壮性、高效性

2.算法与算法分析2

如何评价算法优劣：

在满足正确、健壮、可读下，我们主要考虑算法的效率，即：

• 空间效率：程序所占用的内存

• 时间效率：程序所消耗的时间

  ​ 两种度量方法：

  • 事后统计：受环境影响大，且需要完整的程序去运行（较为麻烦）

  • 事前分析：

    • 算法运行时间 = 一个简单操作所需时间*简单操作次数

    • 也 = 每条语句的执行次数*一次执行的时间

    • 每条语句的执行次数也叫语句频度

    • 每条语句执行的时间是机器本身软硬件环境决定的，与算法无关，因此也叫单位时间

      以矩阵乘法代码为例自己计算一下消耗时间

      for(i=1;i<=n;i++)  //执行频度n+1,i=n+1时要进行一次条件判断操作,所以是n+1,下面操作也是同理
      {
      	for(j=1;j<=n;j++)          //执行频度(n+1)n
      	{
      		x=0;                     //执行频度n^2
      		for(k=1;k<=n;k++)        //执行频度(n+1)n^2
      			x+=a[i][k]*b[k][j];	   //执行频度n^3
      			c[i][j]=x;	           //执行频度n^2
      	}	 	
      } 	
      

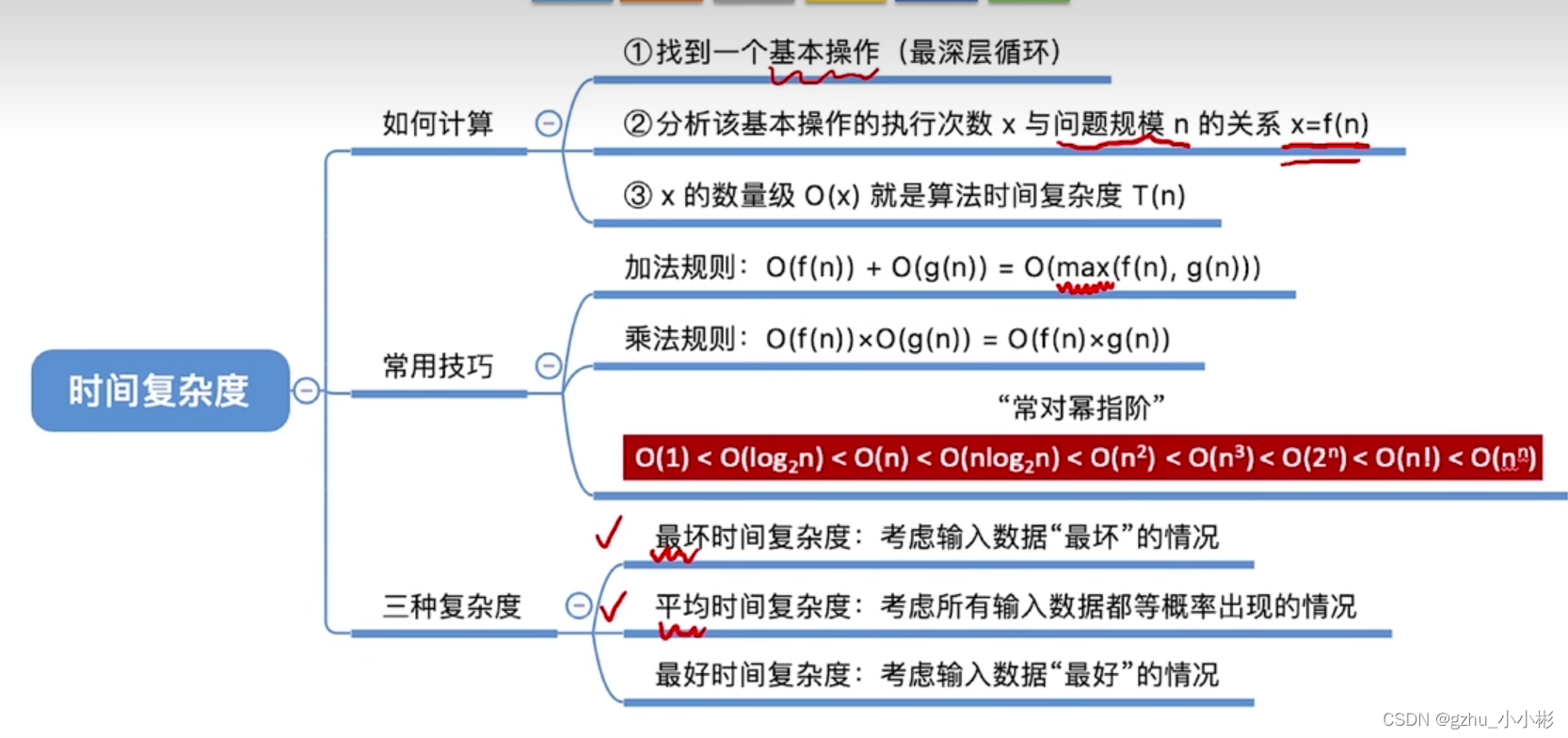
算法的渐进时间复杂度（简称__时间复杂度__）：

• 为了方便比较不同算法的时间效率，我们仅比较其数量级
• 因为我们只比较数量级，所以在计算时只要考虑基本语句的重复次数f(n),T(n)=O(f(n))
• 那么怎样找这些基本语句呢
  • 算法中重复执行次数和算法的执行时间成正比的语句
  • 对算法运行时间贡献最大的语句
  • 执行次数最多

3.算法与算法分析3

怎样简化求时间复杂度的过程：

1. 找出语句频度最大的那条语句作为基本语句
2. 计算基本语句的频度得到f(n)
3. T(n)=O(f(n)),T(n)表示时间复杂度

[时间复杂度详解](详解时间复杂度计算公式(附例题细致讲解过程)_时间复杂度怎么算-优快云博客,具体计算过程和例题

4.算法与算法分析4

算法中基本操作的重复执行次数还随问题的输入数据集不同而不同，如顺序查找法

所以会出现__最坏时间复杂度，平均时间复杂度__，最好时间复杂度

简化方法：

1. 加法规则
2. 乘法规则

---

渐进空间复杂度（空间复杂度）：算法所需存储的度量

空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度。空间复杂度不是程序占用了多少字节的空间，因为这个也没太大意义，所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟时间复杂度类似，也使用大O渐进表示法。

S(n)=O(f(n)) ,n为问题的规模或者大小

算法占据的空间：

		-  算法本身要占据的空间，输入\输出，指令，常量
		-  算法所需的辅助空间

[具体实例](时间复杂度与空间复杂度详解 —— 如何计算 + 如何表示_空间复杂度和时间复杂度-优快云博客)

python练习

1.问题描述
合并两个升序的整数数组A和B,形成一个新的数组，新数组也要有序。
2.问题示例
输入A=[1],B=[1],输出[1,1],返回合并后的数组。输入A=[1,2,3,4],B=[2,4,5,6],输出[1,2,2,3,4,4,5,6],返回合并所有元素后的数组。

def addshuzu(A,B):
    C = list()
    C.extend(A)
    C.extend(B)
    C.sort()
    print(C)

a = [1]
b = [1]
addshuzu(a,b)

c = [1,2,3,4]
d = [2,4,5,6]
addshuzu(c,d)

[1, 4] [1, 2, 3]
[1, 1, 2, 3, 4]
[1, 2, 3, 4] [2, 4, 5, 6]
[1, 2, 2, 3, 4, 4, 5, 6]