在开始前请确保您有一定的LLM基础和强化学习基础😊
如果您没有RL基础我推荐David Sliver的讲座(前三集即可)RL Course by David Silver - Lecture 1: Introduction to Reinforcement Learning - YouTube
如果您还不了解CoT,请看我的这篇文章:从理论到实践:思维链(CoT)提示-优快云博客
叠甲:我对文章中提到的所有算法的数学解析只是片面的,深入研究会在不久的将来发布(也许吧😔),敬请期待😊(欢迎各位大佬指出错误😊)
定义:
多路径生成:通过生成多条独立的推理路径(即不同的解题思路),探索问题的多种潜在解法
- 数学本质:在概率空间中对解空间进行蒙特卡洛采样,覆盖高概率区域
- 目标:降低因单一路径随机错误导致的答案偏差
自洽性:从多条路径中选择逻辑一致、相互支持的答案
- 数学本质:通过统计聚合(如多数投票、加权平均)抑制噪声,逼近真实解
-
目标:将弱推理路径提升为强鲁棒解
数学视角
多路径生成
1.数学定义与概率模型
多路径生成的核心是通过生成多个独立的推理链,探索问题空间的不同可能性
设问题 ,生成
条独立推理链
,每条链对应答案
每条链的生成过程可建模为:
其中 为第
条链的步骤数
2.多路径的优势
覆盖搜索空间:若单链正确概率为 ,则
条链中至少一条正确的概率为:
当 m 增大时,
降低方差:答案的方差随 而下降:
其中 为多路径聚合后的答案
3.多路径生成方法
随机采样:通过调整温度参数 控制多样性:
:增加多样性,生成更多路径
:降低多样性,聚焦高概率路径
束搜索:保留 top-b 个部分路径,逐步扩展:
- 每个时间步选择得分最高的 b 个路径
- 复杂度:
,
为词汇表大小
自洽性
1.自洽性数学目标
定义:不同路径 的最终答案
应收敛到一致结果,最小化错误率:
答案分布的一致性:若模型自洽,不同路径的答案分布应高度集中于某一值 ,即:
概率分布的锐利性:理想情况下,存在 使得:
且
2.自洽性实现方法
多数投票:选择出现频率最高的答案
加权投票:根据路径生成概率赋予权重
3.数学性质分析
- 大数定理:当
,若路径独立且模型校准正确,多数投票结果收敛到真实答案
- 信息熵:答案分布的熵
越小,自洽性越强
示例
有方程组 ,生成3条解方程路径:
1.路径一(消元法):
2.路径二(代入法):
3.路径三(矩阵求逆):
自洽性聚合:
- 多数投票:3条路径均得(
),置信度为100%
- 概率加权:若路径3的矩阵运算概率为0.90,其他路径为0.95,则加权得分:
数学证明
定理1:多路径的信息增益
- 陈述:生成
条路径可将答案的不确定性(熵)降低为:
其中 为互信息,满足
- 证明:
由于观测 提供信息,条件熵
定理2:自洽性的误差指数衰减
- 陈述:若单路径正确率
,则多数投票的错误率以指数速度衰减:
其中 为KL散度
- 证明:应用Chernoff Bound,令
,则:
代码实现
多路径生成
# CoT
def generate_cot_prompt(problem, method=None):
method_hints = {
"algebra": [
"观察方程结构,寻找可消元变量",
"通过加减方程消去一个未知数",
"解出单一变量后回代求解",
"验证解是否满足所有方程"
],
"matrix": [
"将方程组写成矩阵形式AX=B",
"计算系数矩阵A的行列式",
"若行列式不为零,计算逆矩阵A⁻¹",
"通过X=A⁻¹B求解未知数"
],
"default": [
"分析方程组的线性组合可能性",
"选择最简便的消元方法",
"逐步推导并记录中间结果",
"交叉验证所有方程"
]
}
selected_method = method if method in method_hints else "default"
steps = "\n".join([f"{i+1}. {hint}" for i, hint in enumerate(method_hints[selected_method])])
return f"""请严格按以下格式回答:
{problem}
分步思考({selected_method}方法):
{steps}
必须使用XML标签包裹答案:
<solution>
[此处写推导过程,必须包含具体计算步骤]
</solution>
<final_answer>
[此处写最终答案,格式示例:x=3,y=5]
</final_answer>"""
# 多路径生成
def multi_path_generation(problem, num_paths=3):
methods = ["algebra", "matrix", "default"]
paths = []
for i in range(num_paths):
method = methods[i % len(methods)]
prompt = generate_cot_prompt(problem, method)
inputs = tokenizer(prompt, return_tensors="pt", padding=True, truncation=True).to(model.device)
# 生成参数优化
outputs = model.generate(
inputs.input_ids,
max_new_tokens=512,
temperature=0.7 + 0.15*i,
top_p=0.92,
do_sample=True,
num_return_sequences=1,
eos_token_id=tokenizer.eos_token_id,
pad_token_id=tokenizer.eos_token_id,
repetition_penalty=1.1
)
full_text = tokenizer.decode(outputs[0], skip_special_tokens=True)
if "</final_answer>" in full_text:
paths.append(full_text)
return paths自洽性验证
def self_consistency_check(paths):
answer_pattern = r"<final_answer>([\s\S]*?)</final_answer>"
answer_counter = Counter()
for path in paths:
match = re.search(answer_pattern, path, re.IGNORECASE)
if match:
raw_answer = match.group(1)
cleaned = re.sub(r"[^0-9a-zA-Z=,]", "", raw_answer)
cleaned = re.sub(r"([a-zA-Z])=", r"\1=", cleaned)
answer_counter[cleaned.lower()] += 1
# 多数投票需超过60%
if answer_counter:
most_common = answer_counter.most_common(1)[0]
return most_common[0] if most_common[1] > len(paths)*0.6 else None
return None数学验证
def mathematical_verification(problem, answer):
try:
problem_clean = re.sub(r"[\u2010-\u2015\-]", "-", problem)
problem_clean = re.sub(r"解方程组:|方程\d+[::]\s*", ";", problem_clean)
problem_clean = re.sub(r"[^0-9xyab=+\-*/();]", " ", problem_clean)
problem_clean = re.sub(r"(\d)([xyab])", r"\1*\2", problem_clean)
problem_clean = re.sub(r"\s+", " ", problem_clean).strip()
problem_clean = re.sub(r";+", ";", problem_clean).strip(';')
equations = []
equation_strings = [eq.strip() for eq in problem_clean.split(';') if eq.strip()]
for eq_str in equation_strings:
match = re.match(r"^\s*([^=]+?)\s*=\s*(.+?)\s*$", eq_str)
if not match:
print(f"方程格式错误: {eq_str}")
return False
lhs, rhs = match.groups()
try:
equations.append(Eq(sympify(lhs), sympify(rhs)))
except Exception as e:
print(f"方程解析失败: {lhs} = {rhs},错误: {e}")
return False
answer_dict = {}
for pair in answer.split(','):
var, val = pair.split('=')
var = var.strip().lower()
answer_dict[symbols(var)] = float(val)
return all(eq.subs(answer_dict) for eq in equations)
except Exception as e:
print(f"验证错误: {str(e)}")
return False结果
========================================
处理问题: 解方程组: 方程1: x + y = 8 方程2: 2x - y = 1
========================================
生成有效路径数: 5/5
示例路径 1:
------------------------------
请严格按以下格式回答:
解方程组: 方程1: x + y = 8 方程2: 2x - y = 1
分步思考(algebra方法):
1. 观察方程结构,寻找可消元变量
2. 通过加减方程消去一个未知数
3. 解出单一变量后回代求解
4. 验证解是否满足所有方程
必须使用XML标签包裹答案:
<solution>
[此处写推导过程,必须包含具体计算步骤]
</solution>
<final_answer>
[此处写最终答案,格式示例:x=3,y=5]
</final_answer>">
</think>
### 分步思考
#### 1. 观察方程结构,寻找可消元变量
在给定的两个方程中,我们可以选择消去其中一个变量。观察发现,通过将两个方程相加可以消去 \( y \)。
- 方程1: \( x + y = 8 \)
- 方程2: \( 2x - y = 1 \)
#### 2. 通过加减方程消去一个未知数
将方程1和方程2相加:
\[
(x + y) + (2x - y) = 8 + 1 \\
3x = 9
\]
#### 3. 解出单一变量后回代求解
从上述等式中解得:
\[
x = 3
\]
将 \( x = 3 \) 代入方程1:
\[
3 + y = 8 \\
y = 5
\]
#### 4. 验证解是否满足所有方程
将 \( x = 3 \) 和 \( y = 5 \) 代入方程2验证:
\[
2(3) - 5 = 6 - 5 = 1
\]
结果正确。
---
### 最终答案
\( x = \boxed{3} \), \( y = \boxed{5} \)
示例路径 2:
------------------------------
请严格按以下格式回答:
解方程组: 方程1: x + y = 8 方程2: 2x - y = 1
分步思考(matrix方法):
1. 将方程组写成矩阵形式AX=B
2. 计算系数矩阵A的行列式
3. 若行列式不为零,计算逆矩阵A⁻¹
4. 通过X=A⁻¹B求解未知数
必须使用XML标签包裹答案:
<solution>
[此处写推导过程,必须包含具体计算步骤]
</solution>
<final_answer>
[此处写最终答案,格式示例:x=3,y=5]
</final_answer>>
</think>
### 解方程组
#### 分步思考(矩阵方法)
**1. 将方程组写成矩阵形式 \( AX = B \)**
给定的方程组为:
\[
\begin{cases}
x + y = 8 \\
2x - y = 1
\end{cases}
\]
将其表示为矩阵形式 \( AX = B \),其中:
\[
A = \begin{bmatrix} 1 & 1 \\ 2 & -1 \end{bmatrix}, \quad X = \begin{bmatrix} x \\ y \end{bmatrix}, \quad B = \begin{bmatrix} 8 \\ 1 \end{bmatrix}
\]
所以:
\[
AX = \begin{bmatrix} 1 & 1 \\ 2 & -1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 8 \\ 1 \end{bmatrix} = B
\]
**2. 计算系数矩阵 \( A \) 的行列式**
系数矩阵 \( A \) 的行列式为:
\[
|A| = (1)(-1) - (1)(2) = -1 - 2 = -3
\]
**3. 计算逆矩阵 \( A^{-1} \)**
由于行列式 \( |A| \neq 0 \),逆矩阵存在。逆矩阵公式为:
\[
A^{-1} = \frac{1}{|A|} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}
\]
其中,\( A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \)
代入数据:
\[
A^{-1} = \frac{1}{-3} \begin{bmatrix} -1 & -1 \\ -2 & 1 \end{bmatrix} = \begin{bmatrix} \frac{1}{3} & \frac{1}{3} \\ \frac{2}{3} & -\frac{1}{3} \end{bmatrix}
\]
**4. 通过 \( X = A^{-1}B \) 求解未知数**
将 \( A^{-1} \) 和 \( B \) 代入:
\
自洽性选择结果: x=3,y=5
数学验证结果: ✅ 通过
可视化结果已保存至 equation_visualization.png
最终结果: 验证通过 ✅
答案: x=3,y=5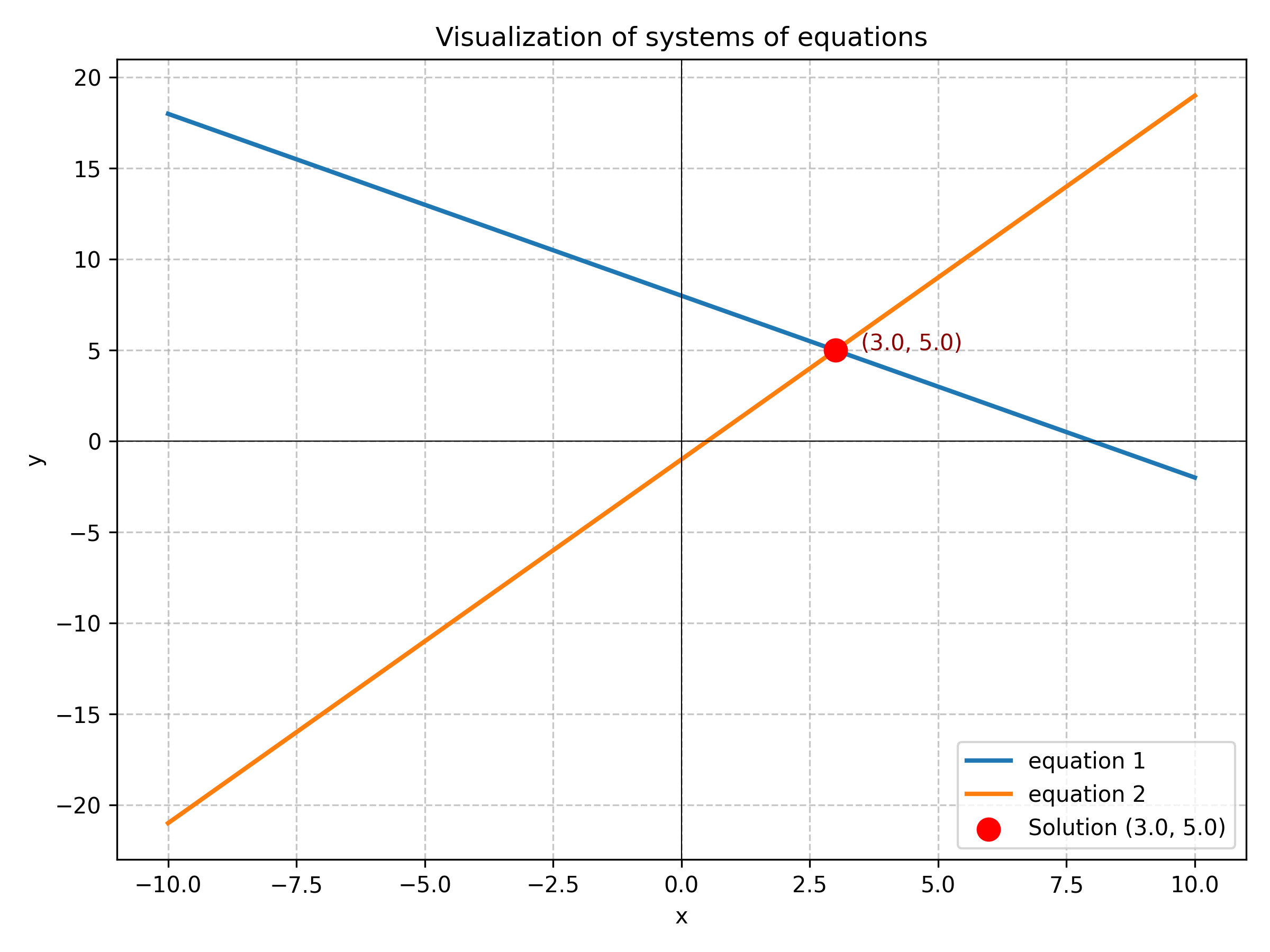
完整代码实现请见我的github仓库:naidezhujimo/CoT-multi-path-generation-and-self-consistency




















 757
757

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








