除了最小生成树,图还有一项重要的应用,就是求最短路劲
这篇博客分享一下最短路径的三大算法
简述
最短路径问题:从在带权有向图G中的某一顶点出发,找出一条通往另一顶点的最短路径,最短也就是
沿路径各边的权值总和达到最小。
简单来说,就是求两个顶点间的最短路劲
求最短路劲主要有三种经典的算法
分别是:
- Dijkstra算法
- Bellman-ford算法
- Floyd-Warshall算法
其中前两种都是求单源最短路径,第三种是求多源最短路径
求最短路径的前置条件
求最短路径,我们肯定需要将最短路径的长度存起来,并且把最短路径的路径存起来
存最短路径的长度很简单,直接使用数组dis就行
而存最短路径的路径怎么办呢?
这里提供一个比较好的方法,我们可以采用双亲表示法,我们用数组parentPath,存路径中上一个顶点即可,这样依次往前走,就能将完整的最短路径确定下来
Dijkstra算法
Dijkstra算法是最高效的求单源最短路的算法,
核心思想和最小生成树中的Prim算法相似,都是采用局部贪心的策略
因为是求单源最短路径,单源是什么意思呢?
单源就是只有一个起点,也就是说,Dijkstra算法是求一个起点到其他所有点的最短路径
Dijkstra算法思想
那么Dijkstra算法怎么执行呢?
针对一个带权有向图G,将所有结点分为两组S和Q,S是已经确定最短路径的结点集合,在初始时
为空(初始时就可以将源节点s放入,毕竟源节点到自己的代价是0),Q 为其余未确定最短路径
的结点集合,每次从Q 中找出一个起点到该结点代价最小的结点u ,将u 从Q 中移出,并放入S
中,对u 的每一个相邻结点v 进行松弛操作。松弛即对每一个相邻结点v ,判断源节点s到结点u
的代价与u 到v 的代价之和是否比原来s 到v 的代价更小,若代价比原来小则要将s 到v 的代价更新
为s 到u 与u 到v 的代价之和,否则维持原样。如此一直循环直至集合Q 为空,即所有节点都已经
查找过一遍并确定了最短路径,至于一些起点到达不了的结点在算法循环后其代价仍为初始设定
的值,不发生变化。Dijkstra算法每次都是选择V-S中最小的路径节点来进行更新,并加入S中,所
以该算法使用的是贪心策略。
根据思想,可以知道Dijkstra算法的时间复杂度是O(N2)
这官方的说法还是比较抽象的
说人话,其实就是,找最短起始边
路径中会经过很多点,假设起点是i , 终点是j, 起点下一个点是k
Dijkstra算法就是通过将每一次的i到k的距离缩到最小来控制i到j之间成为最短路径的。
Dijkstra算法步骤
OK,我们来细致讲一下算法步骤
首先,我们将所有顶点分成两个集合,
一个集合X是确定了最短路径,另一个集合没有确定最短路径
我们每次都去遍历dis数组,去拿其中最小的一个边,作为i到k,并且这个k不能是X中已经确定了最短路径的顶点
然后,用这个i到k去更新与k相连的所有顶点,
之后,k就完成了他的使命,可以放到集合X中了。
Dijkstra算法的缺陷
Dijkstra算法根据他的思想,是无法处理带负权值的图的,如果有负权值,那么已经进入了X集合中的顶点,依然可能被重新更新,就使得算法失败了。(这个画个图很容易理解的)
Dijkstra算法代码
void Dijkstra(const V& src, vector<W>& dis, vector<int>& parentpath)
{
int srci = getindex(src);
int n = _vertexs.size();
dis.resize(n, MAX_W);
parentpath.resize(n, -1);//初始化
set<int> x;//最开始起点也不妨到X集合中
dis[srci] = W();
parentpath[srci] = srci;
for (int i = 0; i < n; ++i)
{
int min = MAX_W;
int minindex = -1;
for (int i = 0; i < n; ++i)//确定最短的i到k
{
if (dis[i] < min && x.count(i) == 0)
{
min = dis[i];
minindex = i;
}
}
for (int i = 0; i < n; ++i)//更新所有的k到j
{
if (_weights[minindex][i] != MAX_W && dis[minindex] + _weights[minindex][i] < dis[i] && x.count(i) == 0)
{
dis[i] = dis[minindex] + _weights[minindex][i];
parentpath[i] = minindex;
}
}
x.insert(minindex);//k完成了使命,放到X集合中
}
}
Dijkstra算法测试
测试代码
void TestGraphDijkstra()
{
const char* str = "syztx";
graph<char, int, INT_MAX, true> g(str, strlen(str));
g.AddEdge('s', 't', 10);
g.AddEdge('s', 'y', 5);
g.AddEdge('y', 't', 3);
g.AddEdge('y', 'x', 9);
g.AddEdge('y', 'z', 2);
g.AddEdge('z', 's', 7);
g.AddEdge('z', 'x', 6);
g.AddEdge('t', 'y', 2);
g.AddEdge('t', 'x', 1);
g.AddEdge('x', 'z', 4);
vector<int> dist;
vector<int> parentPath;
g.Dijkstra('s', dist, parentPath);
g.PrintShortPath('s', dist, parentPath);
// 图中带有负权路径时,贪心策略则失效了。
// 测试结果可以看到s->t->y之间的最短路径没更新出来
/*const char* str = "sytx";
graph<char, int, INT_MAX, true> g(str, strlen(str));
g.AddEdge('s', 't', 10);
g.AddEdge('s', 'y', 5);
g.AddEdge('t', 'y', -7);
g.AddEdge('y', 'x', 3);
vector<int> dist;
vector<int> parentPath;
g.Dijkstra('s', dist, parentPath);
g.PrintShortPath('s', dist, parentPath);*/
}
}
代码对应的图

测试结果
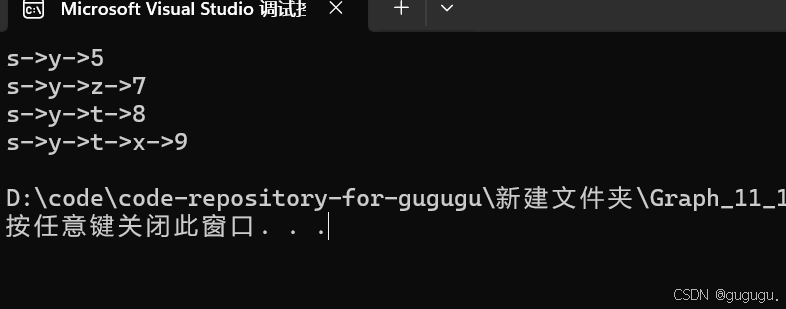
Bellman-ford算法
上文中说到了,Dijkstra算法无法处理带负权值的图,
Bellman-ford算法就是弥补这一缺陷的,bellman-ford算法可以处理带负权值的图。
还是那句话,天下没有白吃的午餐,
bellman-ford也因此时间复杂度更高,达到了O(N3)
Bellman-ford算法思想
bellman-ford算法其实就是一个暴力算法
无脑暴力遍历
Dijkstra算法是去找最短起始边,而Bellman-ford算法是去找最短终止边
在Bellman-ford算法中,我们令起点是i,终点是j,距离j最近的顶点为k
也就是,我们要通过使每一次k到j最小去得到i到j的最短路径
Bellman-ford算法步骤
我们首先要将与给定的起点相连的所有边全部更新到dis数组和parentPath数组中
不然我们暴力全是无穷大,咋搞,哈哈哈
然后我们就开始暴力了。
我们让每个点都要做为k和j,显然这就是两层循环了
当dis[k] + _weights[k][j] < dis[j] 的时候就要更新dis[j]和parentPath[j]了,当然这一操作需要k 和 j相连才能操作
那这样的话,时间复杂度不就是O(N2)吗?
为啥说是O(N3)呢?
所以算法到这里并没有结束
我们来想这么一个场景,上面确定了k到j是最短终止边,
当k成为了j的时候,k的最短终止边又发生了改变怎么办
也就是确定了k到j,但是i到k并没有确定,
所以我们需要再外面再套一层循环,去更新。
当然,这里我们可以借助冒泡排序的思想,设置一个标志,如果标志没有发生改变,就说明k的最短终止边没有改变,就不在需要继续最外面的循环,可以直接结束。
bellman-ford算法无法处理负权回路
注意:虽然bellman-ford算法能够处理负权值的图,但是无法处理负权回路
那么什么是负权回路呢?
负权回路就是有一个环,这个环的权值和是负的
如果出现了负权回路,按照bellman-ford的思想,负权回路的最短路径应该是-∞,所以处理不了这种情况
那么如何判断负权回路呢?
很简单,在走完了三重循环之后,再来一次,如果发生了更新,则说明出现了负权回路。
Bellman-ford算法代码
bool Bellman_Ford(const V& src, vector<W>& dis, vector<int>& parentpath)
{
int srci = getindex(src);
int n = _vertexs.size();
dis.resize(n, MAX_W);
parentpath.resize(n, -1);
dis[srci] = W();
parentpath[srci] = srci;
for (int i = 0; i < n; ++i)//将与起点相连的边全部提前更新一下
{
if (_weights[srci][i] != MAX_W)
{
dis[i] = _weights[srci][i];
parentpath[i] = srci;
}
}
for (int k = 0; k < n; ++k)//算法核心
{
int flag = 0;//标志
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < n; ++j)
{
if (_weights[i][j] != MAX_W && dis[i] + _weights[i][j] < dis[j])
{
dis[j] = dis[i] + _weights[i][j];
parentpath[j] = i;
flag = 1;
}
}
}
if (flag == 0)
break;
}
for (int i = 0; i < n; ++i)//检查是否带有负权回路
{
for (int j = 0; j < n; ++j)
{
if (_weights[i][j] != MAX_W && dis[i] + _weights[i][j] < dis[j])
{
return false;
}
}
}
return true;
}
Bellman-ford算法测试
测试代码
void TestGraphBellmanFord()
{
const char* str = "syztx";
graph<char, int, INT_MAX, true> g(str, strlen(str));
g.AddEdge('s', 't', 6);
g.AddEdge('s', 'y', 7);
g.AddEdge('y', 'z', 9);
g.AddEdge('y', 'x', -3);
g.AddEdge('z', 's', 2);
g.AddEdge('z', 'x', 7);
g.AddEdge('t', 'x', 5);
g.AddEdge('t', 'y', 8);
g.AddEdge('t', 'z', -4);
g.AddEdge('x', 't', -2);
vector<int> dist;
vector<int> parentPath;
g.Bellman_Ford('s', dist, parentPath);
g.PrintShortPath('s', dist, parentPath);
//const char* str = "syztx";
//graph<char, int, INT_MAX, true> g(str, strlen(str));
//g.AddEdge('s', 't', 6);
//g.AddEdge('s', 'y', 7);
//g.AddEdge('y', 'z', 9);
//g.AddEdge('y', 'x', -3);
//g.AddEdge('y', 's', 1); // 新增
//g.AddEdge('z', 's', 2);
//g.AddEdge('z', 'x', 7);
//g.AddEdge('t', 'x', 5);
g.AddEdge('t', 'y', -8); //更改
//g.AddEdge('t', 'y', -8);
//g.AddEdge('t', 'z', -4);
//g.AddEdge('x', 't', -2);
//vector<int> dist;
//vector<int> parentPath;
//if (g.Bellman_Ford('s', dist, parentPath))
// g.PrintShortPath('s', dist, parentPath);
//else
// cout << "带负权回路" << endl;
}
测试代码对应的图

测试结果

Bellman-ford算法的优化
Bellman-ford算法三重循环的时间复杂度有点高
所以呢,大佬们研究出来了一些优化的方法
其中最出名的就是SFPA算法
核心就是,每一次出现更新的时候,都把这个顶点入队列,
每次取队头,去更新与队头顶点相连的顶点。
直到队列为空
有兴趣的小伙伴可以自行研究
Floyd-Warshall算法
Floyd-Warshall算法是求多源最短路径的算法
所谓多源,就是可以求任意两个顶点的最短路径。
所以,我们需要用二维数组来存最短路径的距离(vvdis)和最短路径的路径的上一个顶点(vvparentPath)。
Floyd-Warshall算法思想
Floyd-Warshall算法核心就是动态规划
状态转移方程如下

其实就是有一个中间节点,但是中间节点不知道是哪个节点,
假设起点i,终点j,中间节点k
看vvdis[i][k] + vvdis[k][j] 和 vvdis[i][j] 哪个更小,最短路径就是这中间更新的那一个
所以,我们需要遍历k,由于要求任意两个点之间的最短路径,所以i和j要需要遍历。
因此时间复杂度也是O(N3)
Floyd-Warshall算法步骤
首先把图中相连的所有边,全部更新到vvdis和vvparentPath中
接着三重循环k i j遍历
如果vvdis[i][k] + vvdis[k][j] < vvdis[i][j] ,就去更新i到j的最短路径。
就是这么简单
Floyd-Warshall算法代码
void Floyd_Warshall(vector<vector<W>>& vvdis, vector<vector<int>>& vvparentpath)
{
int n = _vertexs.size();
vvdis.resize(n);
vvparentpath.resize(n);
for (int i = 0; i < n; ++i)
{
vvdis[i].resize(n, MAX_W);
vvparentpath[i].resize(n, -1);
}
for (int i = 0; i < n; ++i)//初始化
{
for (int j = 0; j < n; ++j)
{
if (_weights[i][j] != MAX_W)
{
if (i == j)
{
vvdis[i][j] = W();
vvparentpath[i][j] = i;
}
else
{
vvdis[i][j] = _weights[i][j];
vvparentpath[i][j] = i;
}
}
}
}
for (int k = 0; k < n; ++k)
{
for (int i = 0; i < n; ++i)
{
for (int j = 0; j < n; ++j)
{
//不加上vvdis[i][k] != MAX_W在运算的时候可能会超出int的范围
if (vvdis[i][k] != MAX_W && vvdis[k][j] != MAX_W && vvdis[i][k] + vvdis[k][j] < vvdis[i][j])
{
vvdis[i][j] = vvdis[i][k] + vvdis[k][j];
vvparentpath[i][j] = vvparentpath[k][j];
}
}
}
}
}
Floyd-Warshall算法测试
测试代码
void TestFloydWarShall()
{
const char* str = "12345";
graph<char, int, INT_MAX, true> g(str, strlen(str));
g.AddEdge('1', '2', 3);
g.AddEdge('1', '3', 8);
g.AddEdge('1', '5', -4);
g.AddEdge('2', '4', 1);
g.AddEdge('2', '5', 7);
g.AddEdge('3', '2', 4);
g.AddEdge('4', '1', 2);
g.AddEdge('4', '3', -5);
g.AddEdge('5', '4', 6);
vector<vector<int>> vvDist;
vector<vector<int>> vvParentPath;
g.Floyd_Warshall(vvDist, vvParentPath);
// 打印任意两点之间的最短路径
for (size_t i = 0; i < strlen(str); ++i)
{
g.PrintShortPath(str[i], vvDist[i], vvParentPath[i]);
cout << endl;
}
}
测试代码对应的图

测试结果

























 3552
3552

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








