opencv#26 直方图匹配

      图像直方图均衡化是将原有的图像直方图的分布形式调整的更为均匀，而如果我希望将图像直方图的分布形式调整的更加集中在某个区域上，那么图像直方图均衡化是没办法实现这个功能的，这就需要本节介绍的内容：直方图匹配。

直方图匹配原理

      直方图匹配就是将原有的图像直方图的分布形式指定/映射/匹配为所需要的分布形式，这个分布形式可以人为的给出，或者从图像中获得。

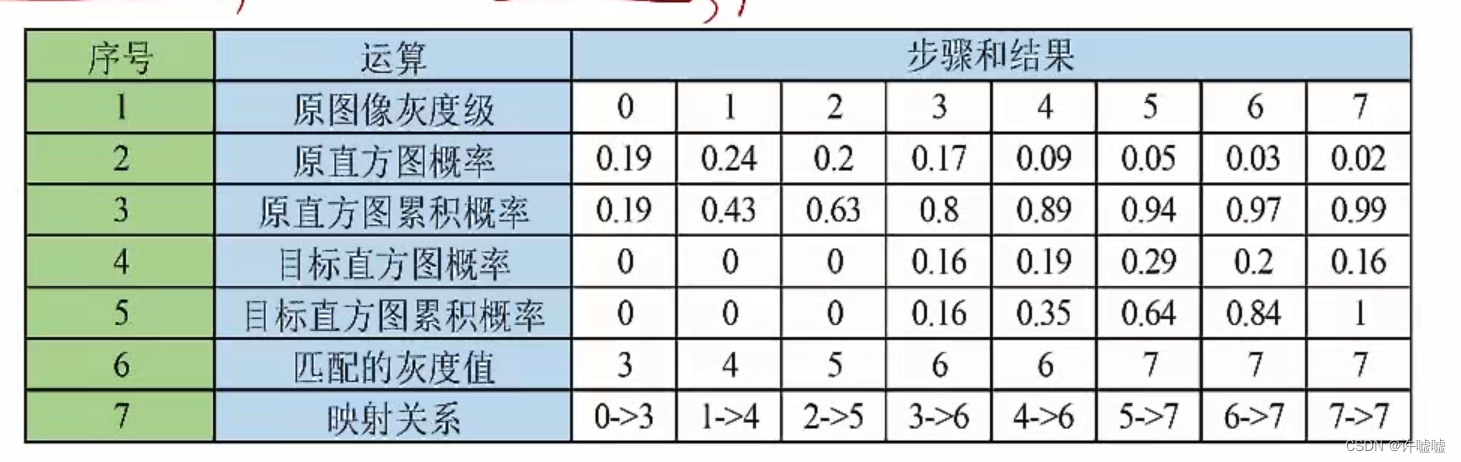
      图像直方图累计概率就是将每个像素值的概率叠加起来，比如图像像素为3的累计概率就是图像像素为1，2，3这三个像素值的概率之和，就得到了累计图像概率。

      图像直方图累计概率作用：通过原图像中某个像素的累积概率与目标图像中的像素的某个概率进行比较，若两者相等，也就是不需要对其改变，若不等，比如原图像的累积概率<目标图像累积概率，那么我们就需要将更多的像素映射为目标图像中的像素，以补充原图像中某个像素的累积概率与目标图像更为接近，从而实现 将分布形式调整为一致。

      那么为什么不使用每个像素的概率而使用累计像素的概念呢？是因为在图像的直方图分布中可能会出现某个像素值是不存在的情况，那么此像素值的概率就为0，如何将这个像素进行映射呢，这个状况是不好判断的。因此我们使用的是累积概率。

      我们观察上表，原直方图累积概率分布较为平缓，而目标图像累积概率更为集中在像素值较大的区域，要将分布较为平缓的映射为分布较为陡峭的形式，我们首先比较像素值为0的累积概率是0.19，目标图像中像素值为0的累计概率为0，但我们不能将像素值为0的映射为没有，目标图像中像素值为1和2的累积概率均为0，因此也不能将0映射为1和2，目标图像中像素值为3的累积概率是0.16，原图像中像素值为0的累积概率与目标图像中像素值为3的累计概率比较接近，也就是我将原图像中像素值为0的映射到目标图像中像素值为3的才比较合理;原图像像素值为1的累积概率为0.43，而目标图像中更接近的是像素值为4的累积概率，因此将原图像中的1映射为4，后面以此类推...这样依次比较，便可以得到我们原图像中每一个像素应该匹配或者映射为什么像素值，通过这样的形式得到的映射关系就是直方图匹配的过程。

     为了寻找原图像中累计概率与目标中的哪个概率更为接近，我们可以将原图像中的每一个累计概率与目标中的累计概率相减取绝对值，两者之间的最小值便是我们的映射关系，我们可以得到一个二维矩阵，在矩阵中，每一横行存放的是原图像与目标图像的像素的累积概率之差，寻找每一横行中的最小值，便可以得到映射关系，得到映射关系后我们可以借助Lut的映射关系，将图像进行映射，从而实现图像的匹配。整个过程大概可以分为三个步骤：1.构建插值矩阵。2.寻找插值矩阵每一行最小值，得到Lut映射关系。3.应用Lut实现图像的直方图匹配。

     在opencv中没有提供专门用于直方图匹配的函数，因此整个过程需要我们自己去书写函数，实现这三个步骤，从而实现直方图匹配。

#include <opencv2/opencv.hpp>
#include <iostream>

using namespace cv; //opencv的命名空间
using namespace std;

void drawHist(Mat& hist, int type, string name);//归一化并绘制直方图函数
//主函数
int main()
{
	Mat img11 = imread("E:/opencv/opencv-4.6.0-vc14_vc15/opencv/123.jpg");
	Mat img22 = imread("E:/opencv/opencv-4.6.0-vc14_vc15/opencv/lenac.png");

	Mat img1, img2;
	cvtColor(img11, img1, COLOR_BGR2GRAY);
	cvtColor(img22, img2, COLOR_BGR2GRAY);

	if (img1.empty() || img2.empty())
	{
		cout << "请确认图像文件名称是否正确" << endl;
		return -1;
	}

	Mat hist1,hist2;//用于存放两张图像的直方图
	//计算两图像直方图
	const int channels[1] = { 0 };
	float inRanges[2] = { 0,255 };
	const float* ranges[1] = { inRanges };
	const int bins[1] = { 256 };
	calcHist(&img1, 1, channels, Mat(), hist1, 1, bins, ranges);//计算原图像直方图
	calcHist(&img2, 1, channels, Mat(), hist2, 1, bins, ranges);//计算均衡化后图像直方图
	//归一化两张图象的直方图
	drawHist(hist1, NORM_INF, "hist1");
	drawHist(hist2, NORM_INF, "hist2");

	//计算两张图像直方图的累积概率
	float hist1_cdf[256] = { hist1.at<float>(0) };
	float hist2_cdf[256] = { hist2.at<float>(0) };
	for (int i = 1; i < 256; i++)
	{
		hist1_cdf[i] = hist1_cdf[i - 1] + hist1.at<float>(i);
		hist2_cdf[i] = hist2_cdf[i - 1] + hist2.at<float>(i);
	}

	//构建累计误差矩阵
	float diff_cdf[256][256];
	for (int i = 0; i < 256; i++)
	{
		for (int j = 0; j < 256; j++)
		{
			diff_cdf[i][j] = fabs(hist1_cdf[i] - hist2_cdf[j]);
		}
	}

	//生成LUT映射表
	Mat lut(1, 256, CV_8U);
	for (int i = 0; i < 256; i++)
	{
		//查找原灰度级为i的映射灰度
		//和i的累积概率差值最小的规定化灰度
		float min = diff_cdf[i][0];
		int index = 0;
		//寻找累积概率误差矩阵中每一行的最小值
		for (int j = 1; j < 256; j++)
		{
			if (min > diff_cdf[i][j])
			{
				min = diff_cdf[i][j];
				index = j;
			}
		}
		lut.at<uchar>(i) = (uchar)index;
	}
	
	Mat result, hist3;
	LUT(img1, lut, result);
	imshow("待匹配图像", img1);
	imshow("匹配的模板图像", img2);
	imshow("直方图匹配结果", result);

	calcHist(&result, 1, channels, Mat(), hist3, 1, bins, ranges); //统计直方图
	drawHist(hist3, NORM_INF, "hist3"); //绘制匹配后的图像直方图


	waitKey(0);//等待函数用于显示图像
	return 0;

}

void drawHist(Mat& hist, int type, string name)//归一化并绘制直方图函数(3个参数分别是：直方图统计结果，需要进行归一化的类型，以及显示图像直方图窗口名称）
{
	int hist_w = 512;
	int hist_h = 400;
	int width = 2;
	Mat histImage = Mat::zeros(hist_h, hist_w, CV_8UC3);
	normalize(hist, hist, 1, 0, type, -1, Mat());
	for (int i = 1; i <= hist.rows; i++)
	{
		rectangle(histImage, Point(width * (i - 1), hist_h - 1),
			Point(width * i - 1, hist_h - cvRound(hist_h * hist.at<float>(i - 1)) - 1),
			Scalar(255, 255, 255), -1);
	}
	imshow(name, histImage);
}