基于 Matlab 的信号和系统实验指导书及实验报告

目录

一、实验指导书

二、实验报告（仅部分）

1.连续时间信号在 Matlab 中的表示

2.连续时间信号在 Matlab 中的运算

3.连续时间 LTI 系统的时域分析

4.傅里叶变换(FT)及其性质

5.连续时间LTI系统的频率特性及频域分析

---

目录

一、实验指导书

链接：https://pan.baidu.com/s/1Wj2yZeIjMNxeWUl4VwIz8A 
提取码：jf6k

二、实验报告（仅部分）

说明：本报告数据及内容均来自网络整理，有错误可留言或自行修改，侵权删。

1.连续时间信号在 Matlab 中的表示

一、  实验原理

1、信号的定义和分类

2、连续信号的表示方法有两种：符号推理法和数值法。

从严格意义上讲，Matlab 数值计算的方法不能处理连续时间信号。然而，可利用连续信号在等时间间隔点的取样值来近似表示连续信号，即当取样时间间隔足够小时，这些离散样值能被 Matlab 处理，并且能较好地近似表示连续信号。

二、  实验目的

1、学会运用 Matlab 表示常用连续时间信号的方法

2、观察并熟悉这些信号的波形和特性

三、  实验环境

Windows10；MATLAB R2021b

四、  实验内容

(1)利用 Matlab 命令画出下列连续信号的波形图。

(a)2cos(3t+π/4)

(b)(2-e-t)u(t)

(c)[1+cos(πt)][u(t)−u(t−2)]

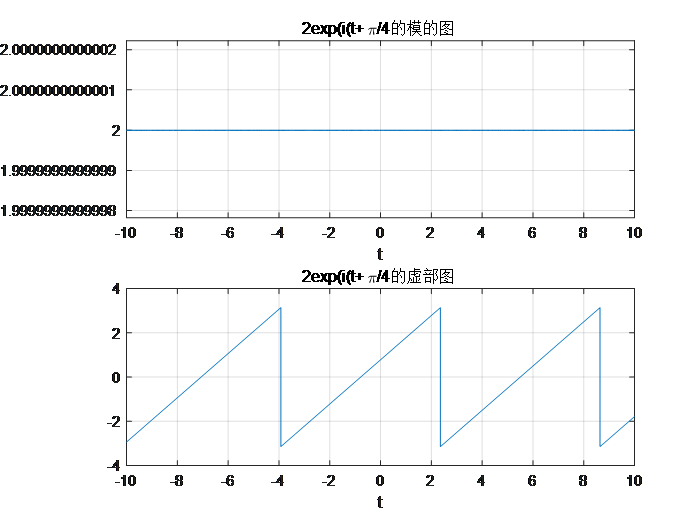
(2)利用 Matlab 命令画出复信号f(t)=2ej(t+π/4)的实部、虚部、模和辐角。

五、  实验数据分析及结果

(1.a)源代码为：

%(2) 2cos(3t+pi/4)

clear;clc;

t=0:0.01:3;

gt=2*cos(3*t+pi/4);

plot(t,gt);grid on

axis([-0.5,3.5,-2.5,2.5]);

title('y=2cos(3t+pi/4)');

(1.b)源代码为：

%(1) (2-e^(-t))ε(t)

clear;clc;

t=0:0.01:3;

ft=2-exp(-t);

plot(t,ft);

grid on;

axis([-0.5,3.5,0.75,2.25]);

title('y=(2-exp(-t))ε(t)');

(1.c)源代码为：

clear;clc;

t=-2:0.01:5;

f1=1+cos(pi*t);

f2=(t>=0)-(t>=2);

ft=f1.*f2;

plot(t,ft)

grid on

 

(2)源代码为：

clc;clear;

t=-10:0.001:10;

y=3*exp(j*(t+pi/4));

real(y);

subplot(2,1,1);

plot(t,ans);

xlabel('t');

title('2exp(i(t+\pi/4的实部图');

grid on;

imag(y);

subplot(2,1,2);

plot(t,ans);

xlabel('t');

title('2exp(i(t+\pi/4的虚部图');

grid on;

clc;clear;

t=-10:0.001:10;

y=2*exp(1i*(t+pi/4));

abs(y);

subplot(2,1,1);

plot(t,ans);

xlabel('t');

title('2exp(i(t+\pi/4的模的图');

grid on;

angle(y);

subplot(2,1,2);

plot(t,ans);

xlabel('t');

title('2exp(i(t+\pi/4的虚部图');

grid on;

六、  实验思考

信号的平移、反转和尺度变换是针对自变量时间而言的，其数学表达式和波形变换中存在着一定的变化规律。从数学表达式上来看，信号的上述所有计算都是自变量的替换过程。所以在使用 Matlab 进行连续时间信号的运算时，只需要