
根据题目我们可以得出用暴力枚举所有的方案会导致一部分样例超时,而暴力方法就是枚举1到n的所有数字,然后每次都进行检查,如果该数是平方数,就直接返回即可
上代码
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#define int long long
using namespace std;
bool check(int n, int i)
{
int k = sqrt(n * i);//定义longlong类型变量,如果开平方根不是整数,那么再开平方就不会等于原来的数
if (k * k == n * i) return true;
return false;
}
signed main(void)
{
int n; cin >> n;
for (int i = 1; i <= n; i++) {
if (check(n, i)) {
cout << i << endl;
return 0;
}
}
return 0;
}
但是会有部分样例无法通过
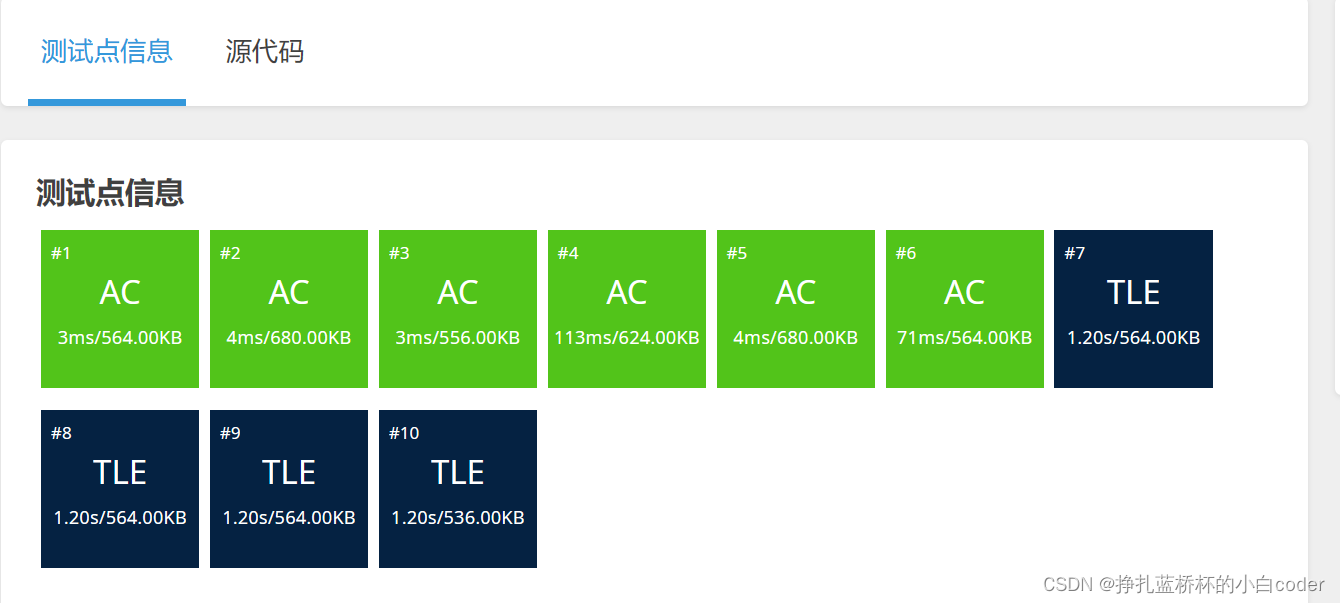
接下来是优化思路:
我们通过观察样例可以发现:12 = 3 * 4 = 3 * 2 * 2; 12 * 3 = 3 * 3 * 2 * 2
15 = 3 * 5, 15 * 15 = 3 * 3 * 5 * 5,当两数相乘分别拆分最小的质因数,并且每个数的数目都是偶次方的时候就是完全平方数,因此我们可以将输入的数进行拆分,并且将奇数次数目的数字进行相乘,将其补充成偶次数目,最后得出的乘数就是答案
上代码
#include<iostream>
#include<cstring>
#include<algorithm>
#include<map>
#define int long long
using namespace std;
signed main(void)
{
int n; cin >> n;
map <int, int> mp;
for (int i = 2; i <= n / i; i++) {
if (n % i == 0) {//如果此时i是n的倍数
while (n % i == 0) {//不断提取,直到i不再是n的倍数
n /= i;
mp[i]++;//统计i出现的次数
}
}
}
if (n > 1) mp[n]++;//如果n最后还大于1,这时候n本身也算一个质因数,因此也要自增
int ans = 1;
for (auto p = mp.begin(); p != mp.end(); p++) {
if ((*p).second % 2 != 0) {//如果某个数的出现次数是奇数次,就直接添加
ans *= (*p).first;
}
}
cout << ans << endl;
return 0;
}
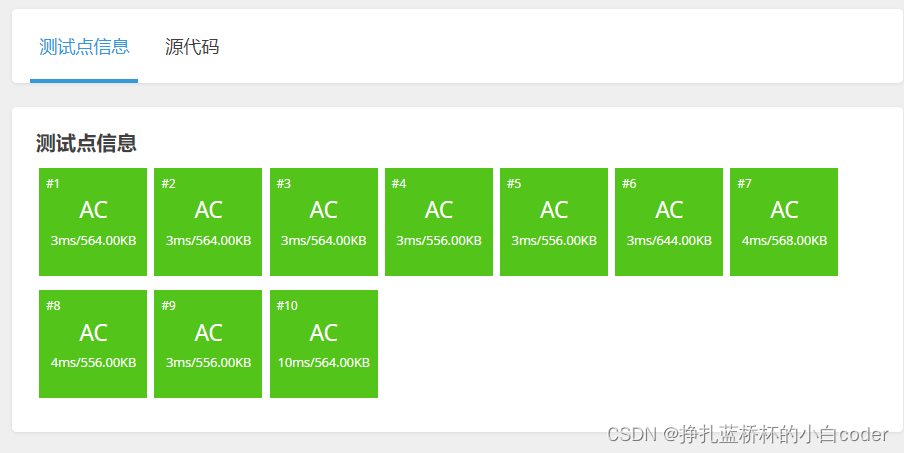







 文章介绍了如何通过观察样例中的模式,避免暴力枚举,利用质因数和次数来判断一个数是否为完全平方数的优化算法。首先,暴力方法检查所有可能的乘积;然后,通过分解输入数并统计质因数出现的次数,若次数为奇数则直接计算答案。
文章介绍了如何通过观察样例中的模式,避免暴力枚举,利用质因数和次数来判断一个数是否为完全平方数的优化算法。首先,暴力方法检查所有可能的乘积;然后,通过分解输入数并统计质因数出现的次数,若次数为奇数则直接计算答案。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








