【笑着写算法系列】“先苦后甜“的前缀和

前言

前缀和一个创建辅助数组帮助我们计算的算法。常见的前缀和的题型都是需要我们直接创建一个前缀和数组方便我们去解决问题，只要前缀和数组创建好后我们对于解决题目会十分简单，且大大减少时间的花费。所以我说它是“先苦后甜”。

一、一维前缀和

代码及其解析：我们这第一题主要让大家理解什么是前缀和，且了解他的基本使用。

如代码，首先我们创建一个数组这，然后在这个数组中存放前i个数的和，如arr[3]中存放a1,a2,a3的和。

这样等循环结束后我们就可以得到一个前缀和数组arr那么这时我们就可以求如题目所讲的al······ar的值

即：arr[r]-arr[l-1]

import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
       int n,q;
       Scanner sc=new Scanner(System.in);
       n=sc.nextInt();
       q=sc.nextInt();
       long[] arr=new long[n+1];

        for(int i=1;i<n+1;i++)
        arr[i]=arr[i-1]+sc.nextInt();
       
       while(q!=0){
        int l,r;
        l=sc.nextInt();
        r=sc.nextInt();
        System.out.println(arr[r]-arr[l-1]);
        q--;
       
       }
          
    }
}

二、二维前缀和

代码及其解析：

首先我们题目要求我们返回其给的两个点(x1,y1),(x2,y2)的对角形成的矩阵和，且这个矩阵以参数的形式进行参与，那么我们是否可以在每一次接收参数时就以（1，1）这个点来作为左上角，以当前的i，j作为右下角将这个矩阵和先进行存储，然后在我们需要求题目给定的两个点(x1,y1),(x2,y2)的对角形成的矩阵和时我们就可以直接通过我们存储好的矩阵和数组进行加减运算得出目标矩阵和了。

import java.util.Scanner;

// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);

        // 注意 hasNext 和 hasNextLine 的区别

        int n = in.nextInt();
        int m = in.nextInt();
        int q = in.nextInt();


        long[][] arr = new long[n + 1][m + 1];

        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++) {
                arr[i][j] = arr[i - 1][j] + arr[i][j - 1] + in.nextInt() - arr[i - 1][j - 1];
            }

        while (q != 0) {
            int x1 = in.nextInt();
            int y1 = in.nextInt();
            int x2 = in.nextInt();
            int y2 = in.nextInt();

            long num = arr[x2][y2] + arr[x1 - 1][y1 - 1] - arr[x2][y1 - 1] - arr[x1 -
                       1][y2];
            System.out.println(num);
            q--;


        }


    }
}

三、寻找数组的中心下标

代码及其解析：

这道题很容易看出我们可以使用前缀和进行解决，但是我们也可以对原本的方式进行优化，我们可以不创建这个前缀和数组，而是只保留当前i的前缀和，然后进行判断时我们的这个前缀和是否等于总的值减去当前i+1的值，这样我们就可以不用在花费空间去创建一个前缀和数组。

import java.util.Arrays;

class Solution {
    public int pivotIndex(int[] nums) {

        int total = Arrays.stream(nums).sum();
        int sum=0;
        for(int i=0;i<nums.length;i++){
            if(sum*2==total-nums[i]) return i;
            sum+=nums[i];

        }

        return -1;
    }
}

四、除自身以外数组的乘积

代码及其解析：

我们这里还是看题了解到我们需要给定一个数组，这个数组等于除当前i的值外，其它数组全部值的乘积。而且题目要求我们不能使用除法那么我们只需要构成连个数组，一个前缀积数组，一个后缀积数组，然后再求结果数组时直接就是前缀乘以后缀即可。

class Solution {
    public int[] productExceptSelf(int[] nums) {
        
        int n=nums.length;
        
        int[] arr=new int[n];

        int[] prev=new int[n];
        int[] tatil=new int[n];

        prev[0]=1;
        tatil[n-1]=1;

        int j=n-2;
        for(int i=1;i<n;i++){
            prev[i]=prev[i-1]*nums[i-1];
            tatil[j]=nums[j+1]*tatil[j+1];
            j--;  
        }

        for(int i=0;i<n;i++){
            arr[i]=prev[i]*tatil[i];
        }

        return arr;


        
    }
}

五、和为k的子数组

代码及其解析：

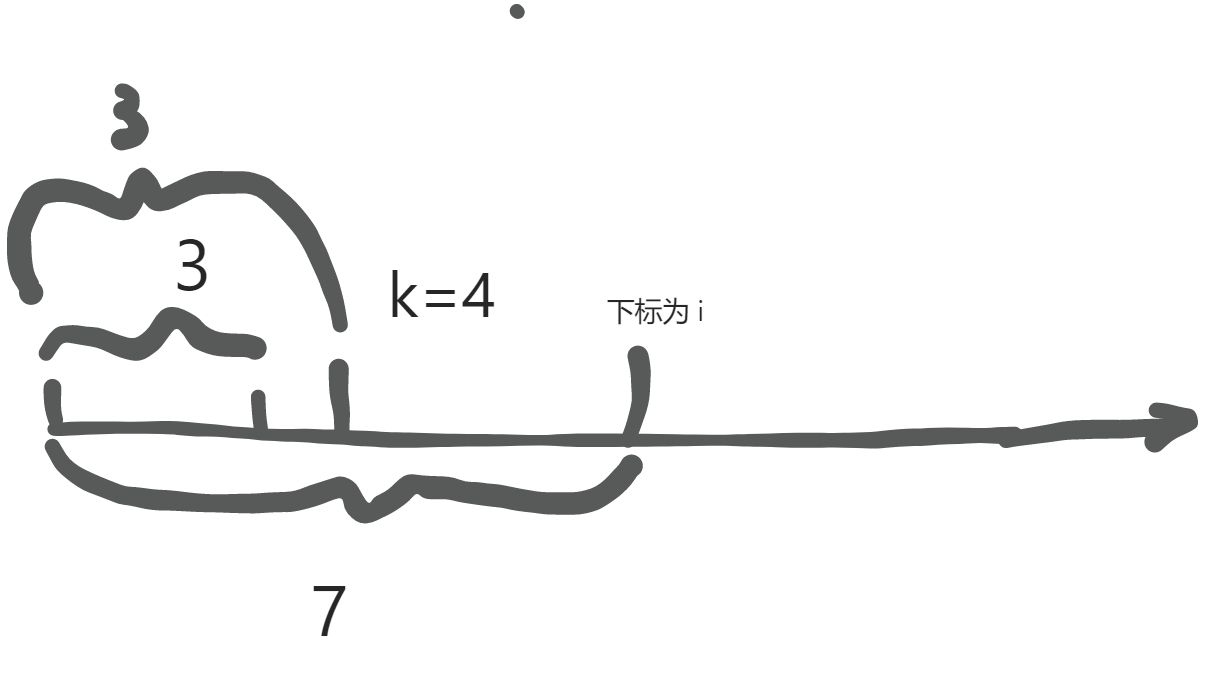
题目要求我们找出有多少个子数组，的和为k，那么我们就可以使用到前缀和了，那么如何判断有多少个呢，首先我们要知道子数组一定是连续的，那么我们要求一段连续数组的值是否为k，那么借助我们的前缀和数组，我们是否就可以使用减法了呢，我们只需要记住当前位置 i （即下标）之前的前缀和，那么我们就用当前的前缀和sum减去k，此时就得到一个数num，我们只需要找再i之前的前缀和是否等于num，如果存在就代表这个num+k=sum。这时就可以证明sum-num后得到的那串数组的和就是k。如图：我们此时包含i之前的前缀和为7，那么我们只需要找7-k（假设k=4）=3的那一段前缀和即可证明，中间那一段的数组就为k，需要注意的是因为原数组中存在负数所以往右走前缀和不一定变大，可能变小，可能变大，也可能不变，所以前缀和为3的数组，可能有多段，也可能没有。

重点：为什么我创建hash后要往hash中put（0，1）呢？这是因为当我们sum刚好就等于k时，我们就会往hash中找是否存在num=0，但是我们可能会找不到所以此时count没有进行加1，会导致结果变小，所以我们要手动加一个num=0的情况进入hash表中。

class Solution {
    public int subarraySum(int[] nums, int k) {
        int sum=0,n=nums.length,count=0;
        HashMap<Integer,Integer> hash=new HashMap<>();
        hash.put(0,1);
        for(int i=0;i<n;i++){
            sum+=nums[i];
            int num=sum-k;
            count+=hash.getOrDefault(num,0);
            hash.put(sum,hash.getOrDefault(sum,0)+1);

        }
        return count;

    }
}

六、和可被k整除的数组

题目解析：与上一题有所不同，这里我们要求的是子数组和可以被k整除的，也就是sum%k==0。

那么这时我们仿照上一道题的思路，使用hash表加前缀和的方法进行处理解决题目，我们可以在hash表中存入每个i位置的前缀和余数，当我们在往后遍历的时候我们在遇到余数相同的时候我们就进行查找这个余数key的vaule进行相加，为什么呢？其实原理与上一题相似，当我们较长的数组余数为k，我们只需要在前面找到余数也为k的子数组将这段子数组减去，那么剩下的数组就不会有余数了。

但是新的问题来了我们在Java中负数也可以取余，也就是我们的取余结果也可能是负数。那么负数对我们解题有什么影响呢？我们看一下面这个例子：

我们如果不处理余数为负数的时候就会出现上面的错误现象，为什么上面的结果为1，而不是2

呢，首先我们单独一个2是一个结果，整个数组也是一个和结果，但是这里只计算了一个结果。其实这里出错的是单独一个2的情况并没有被就算进去，因为我们在往前找【-1，2】同这个sum的余数1时，并没有找到1，但是其实-1也是可以的，为什么呢，因为如果减去-1，那么我们后面的数组就可以理解为sum+1，而此时我们原本的余数sum恰好就差1就可以在凑够一个2，这样就可以整除了。那么我们该如何去改变这个负余数呢，答案就是在负余数的基础上加上k在放进hash表中，这样就是得到一个正数num，这样后面的前缀和在遇到余数刚好为这个正数时，就可以减去这段原本余数为负数的这段数组，这样加相当于给数组加上num，这样就可以使我们的式子合理计算出正确可以被k整除的子数组。

而且数组中的和还有可能是负数，这个负数也是对我们进行计算造成一定影响的

。代码及其解析：

class Solution {
    public int subarraysDivByK(int[] nums, int k) {
        HashMap<Integer,Integer> hash=new HashMap<>();
        hash.put(0,1);
        int count=0,sum=0,n=nums.length,num=0;

       for(int i=0;i<n;i++){
        sum+=nums[i];
        num=(sum%k+k)%k; 
       
        count+= hash.getOrDefault(num,0);
        hash.put(num,hash.getOrDefault(num,0)+1);
        
       }

       return count;
    
    }
}

七、连续数组

代码及其解析：

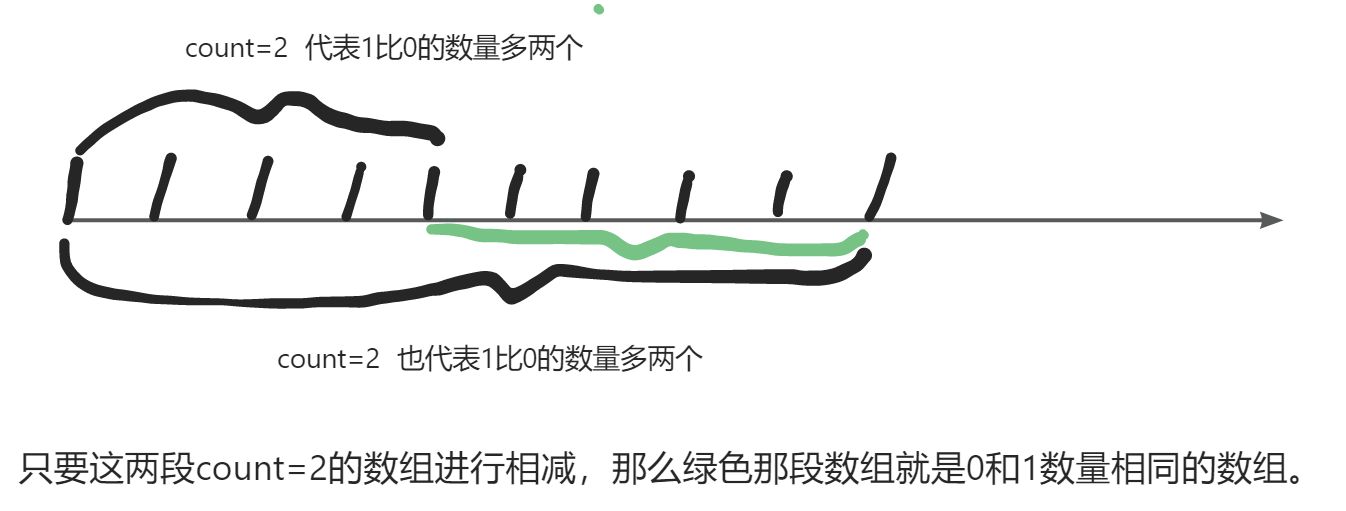
这道题思路还是和前一道题相似，都是使用前缀和，我们将当前i的前缀count的个数进行计数储存到hash表中，注意这里我们计算count的形式是，nums[i]==1的话count++，否则count--。可以这么理解count，count为正数代表1的数量多，为负数则代表0多，等于0代表一样多，因为我们没遍历一个nums[i]都会对count进行计算相加还是相减。那么这时我们在后续的查找中只需要找到同样count的数量的下标n，然后用i-n就是我们一段刚好0和1相同数量的子数组的长度，注意这时不要再把当前（count，i）放进hash表，因为n比较靠前，我们下次再遇到相同的count值时，我们减去n的值更长。

class Solution {
    public int findMaxLength(int[] nums) {
        HashMap<Integer,Integer> hash=new HashMap<>();
        int count=0,len=0;
        for(int i=0;i<nums.length;i++){

            if(nums[i]==1){
                count++;
            }else{
                count--;
            }

            if(count==0)
            {
                len=i+1;
                continue;
            }
            int n=hash.getOrDefault(count,-1);

            if(n!=-1){
                len=Math.max(len,i-n);

            }else{
                hash.put(count,i);
            }


        }
        return len;

    }
}