代码随想录day27 | 贪心算法理论基础 leetcode 455.分发饼干 376.摆动序列 53. 最大子序和

贪心算法理论基础

什么是贪心

贪心的本质是选择每一阶段的局部最优，从而达到全局最优。

贪心算法并没有固定的套路。

所以唯一的难点就是如何通过局部最优，推出整体最优。

贪心算法一般分为如下四步：

• 将问题分解为若干个子问题
• 找出适合的贪心策略
• 求解每一个子问题的最优解
• 将局部最优解堆叠成全局最优解

贪心算法理论基础

什么是贪心

贪心的本质是选择每一阶段的局部最优，从而达到全局最优。

贪心算法并没有固定的套路。

所以唯一的难点就是如何通过局部最优，推出整体最优。

贪心算法一般分为如下四步：

• 将问题分解为若干个子问题
• 找出适合的贪心策略
• 求解每一个子问题的最优解
• 将局部最优解堆叠成全局最优解

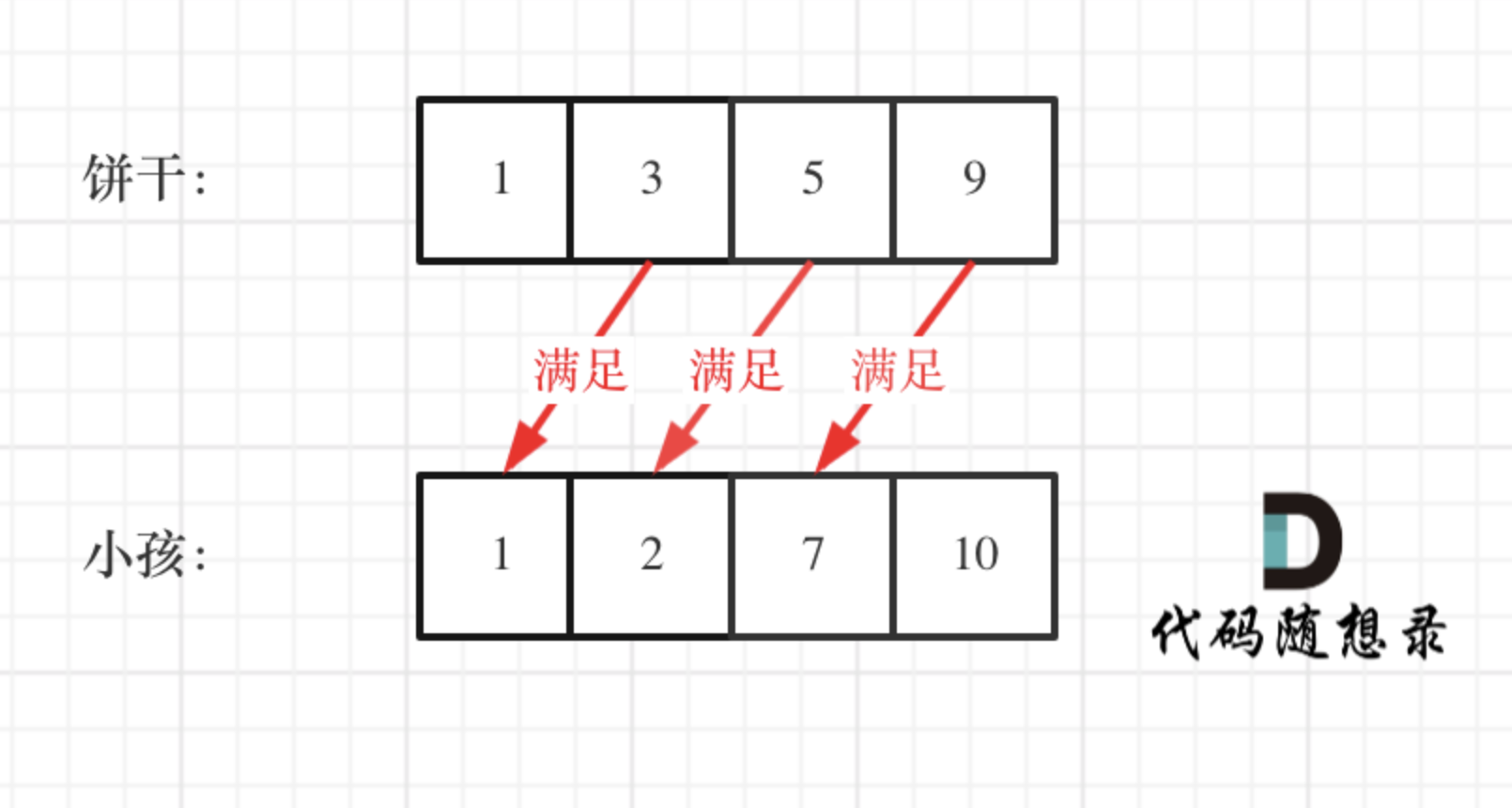
455.分发饼干

Java

class Solution {
    public int findContentChildren(int[] g, int[] s) {
        Arrays.sort(g);
        Arrays.sort(s);
        int count = 0;
        int start = s.length - 1;
        // 遍历胃口
        for (int index = g.length - 1; index >= 0; index--) {
            if(start >= 0 && g[index] <= s[start]) {
                start--;
                count++;
            }
        }
        return count;
    }
}

然后从后向前遍历小孩数组，用大饼干优先满足胃口大的，并统计满足小孩数量。

376.摆动序列

Java

class Solution {
    public int wiggleMaxLength(int[] nums) {
        if (nums.length <= 1) {
            return nums.length;
        }
        //当前差值
        int curDiff = 0;
        //上一个差值
        int preDiff = 0;
        int count = 1;
        for (int i = 1; i < nums.length; i++) {
            //得到当前差值
            curDiff = nums[i] - nums[i - 1];
            //如果当前差值和上一个差值为一正一负
            //等于0的情况表示初始时的preDiff
            if ((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)) {
                count++;
                preDiff = curDiff;
            }
        }
        return count;
    }
}

为什么把 preDiff = curDiff;放在if里面

preDiff = curDiff; 被放在 if 条件内部是因为只有在当前差值满足摆动序列的条件时，才需要更新 preDiff 的值。这么做的原因可以从逻辑和优化两个角度来解释：

1. 逻辑上的原因

preDiff 的作用是记录上一次参与构成摆动序列的有效差值。如果当前的 curDiff 不满足摆动条件（即 (curDiff > 0 && preDiff <= 0) 或 (curDiff < 0 && preDiff >= 0) 不成立），则当前差值无效，不应该用来更新 preDiff。

示例：

假设输入数组为：nums = [1, 7, 7, 4]

• 初始化：preDiff = 0, count = 1
• 第一次：curDiff = 7 - 1 = 6- 条件 (curDiff > 0 && preDiff <= 0) 成立，更新 preDiff = 6，count = 2。
• 第二次：curDiff = 7 - 7 = 0- 条件不成立，因为 curDiff == 0。- 如果此时更新 preDiff = 0，则后续的摆动判断会被错误影响。
• 第三次：curDiff = 4 - 7 = -3- 条件 (curDiff < 0 && preDiff >= 0) 成立，更新 preDiff = -3，count = 3。

因此，只有在当前差值有效时，才需要更新 preDiff。

---

2. 优化上的原因

• 如果 preDiff 总是无条件更新为 curDiff，即使 curDiff 无效（比如差值为 0，或者差值符号未改变），也会浪费计算资源并导致后续的判断失误。
• 放在 if 内部可以避免不必要的更新操作，保证程序的逻辑清晰且效率更高

53. 最大子序和

连续和为零,跳过

Java

class Solution {
    public int maxSubArray(int[] nums) {
        if (nums.length == 1){
            return nums[0];
        }
        int sum = Integer.MIN_VALUE;
        int count = 0;
        for (int i = 0; i < nums.length; i++){
            count += nums[i];
            sum = Math.max(sum, count); // 取区间累计的最大值（相当于不断确定最大子序终止位置）
            if (count <= 0){
                count = 0; // 相当于重置最大子序起始位置，因为遇到负数一定是拉低总和
            }
        }
       return sum;
    }
}

如果全是负数会错误的返回0(count = 0)吗

由于 sum 初始化为 Integer.MIN_VALUE 并且在每次迭代中使用 Math.max 更新，算法能够正确处理全负数的情况，返回数组中最大的负数，而不会返回 0。

具体分析：

1. count = 0 的重置逻辑

在代码中，当 count <= 0 时，count 被重置为 0：

if (count <= 0) {
    count = 0;
}

这意味着当前的累积和 count 已经小于等于零，无法为后续的子序列提供正面贡献，因此将其重置以重新开始计算子序列。但是，这并不会导致错误返回 0，原因如下。

---

2. 为什么不会返回 0：

即使所有元素都是负数，sum 的计算是基于以下逻辑：

sum = Math.max(sum, count);

• sum 的初始值是 Integer.MIN_VALUE（一个极小值）。
• 在每次迭代时，sum 会取当前累积和 count 和已有的最大值 sum 中的较大值。
• 如果 nums 中的所有元素都是负数，count 的最大值也就是数组中的最大负数，而不会是 0。

示例：全是负数的数组

输入：nums = [-4, -2, -5, -8]

1. 初始：sum = Integer.MIN_VALUE, count = 0
2. 第一次迭代：- count += -4 -> count = -4
   • sum = Math.max(Integer.MIN_VALUE, -4) -> sum = -4
   • count <= 0 -> count = 0
3. 第二次迭代：- count += -2 -> count = -2
   • sum = Math.max(-4, -2) -> sum = -2
   • count <= 0 -> count = 0
4. 第三次迭代：- count += -5 -> count = -5
   • sum = Math.max(-2, -5) -> sum = -2
   • count <= 0 -> count = 0
5. 第四次迭代：- count += -8 -> count = -8
   • sum = Math.max(-2, -8) -> sum = -2
   • count <= 0 -> count = 0

最终返回的 sum = -2，即数组中的最大负数。