DP概念和编程方法-优快云博客

本文链接：https://blog.youkuaiyun.com/2302_80869537/article/details/138651845

前言

动态规划(DP)是一种算法技术，它将大问题分解为更简单的子问题，对整体问题的最优解决方案取决于子问题的最优解决方案。动态规划常用于求解计数问题(求方案数)和最值问题(最大价值、最小花费)等。

本节介绍DP的基础知识，包括DP的特征、DP的编程方法、DP状态的设计和状态方程的推导，以及DP的空间优化滚动数组。

1. DP的概念

DP是求解多阶段决策问题最优化的一种算法思想，它用于解决具有重叠子问题、最优子结构特征的问题。

下面以斐波那契数列为例说明DP的概念。

斐波那契数列是一个递推数列，它的每个数字是前面两个数字的和，如1，1，2，3，5，8…计算第n个斐波那契数，递推公式为

fib(n)=fib(n-1)+fib(n-2)

斐波那契数列的一种应用场景是走楼梯问题：一次可以走一个或两个台阶，问走到第n个台阶时，一共有多少种走法?走楼梯问题的数学模型是斐波那契数列。要走到第n级台阶，分为两种情况，一种是从第n-1级台阶走一步过来，另一种是从第n-2级台阶走两步过来。

用递归编程求斐波那契数列，代码如下。

int fib(int n)
{
    if(n==1 || n==2) return 1;
    returhn (fib(n-1)+fib(n-2));
}

代码中的递归以2的倍数递增，复杂度为O(2^n)，非常差。用DP可以优化复杂度。

为了解决总体问题fib(n)，将其分解为两个较小的子问题，即fib(n-1)和fib(n-2)，这就是DP的应用场景。

一些问题具有两个特征：重叠子问题、最优子结构。用DP可以高效率地处理具有这两个特征的问题。

1.1 重叠子问题

首先，子问题是原大问题的小版本，计算步骤完全一样；其次，计算大问题时，需要多次重复计算小问题。这就是重叠子问题。以斐波那契数列为例，递归计算fib(5)，分解为如图所示的子问题。

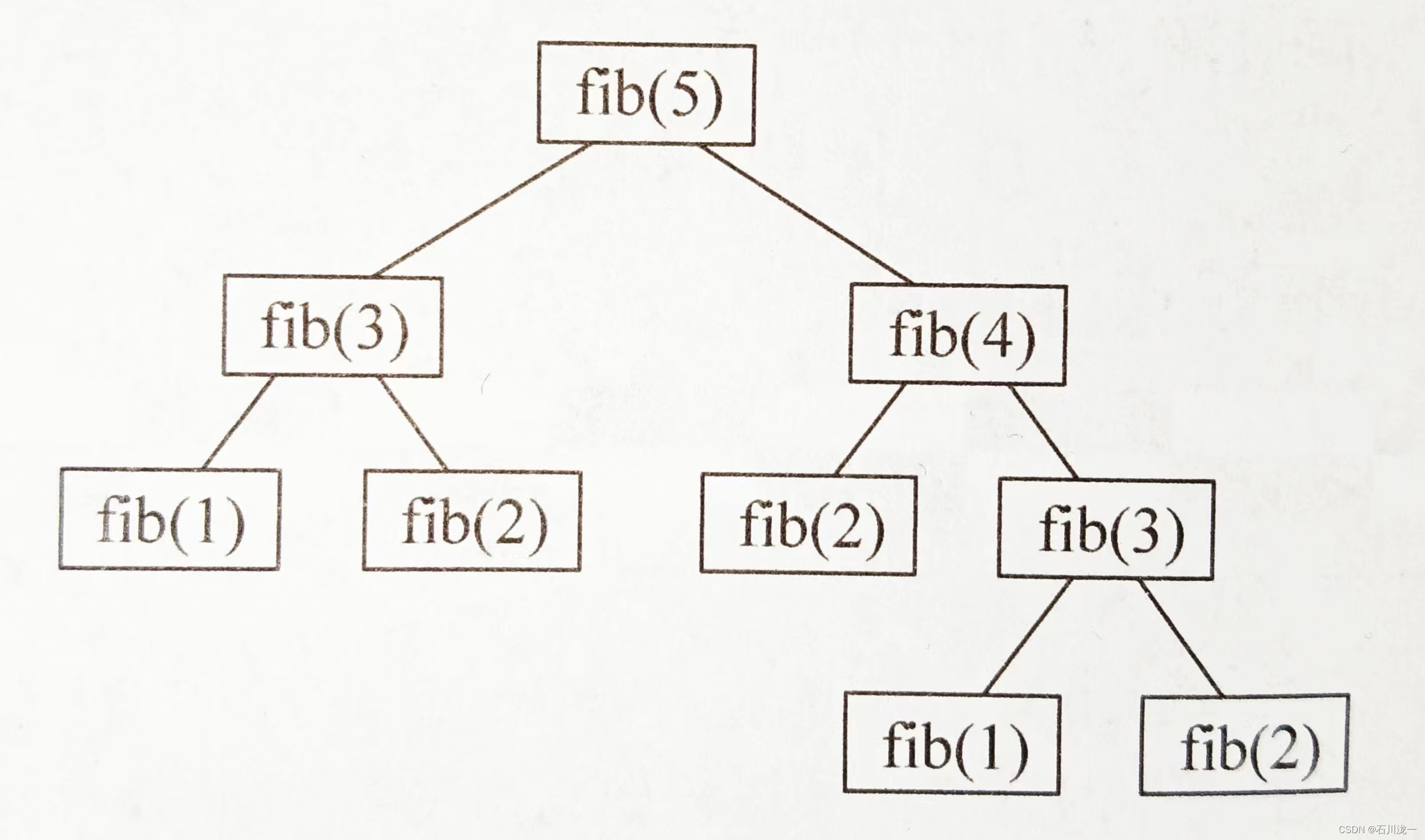
其中fib(3)计算了两次，其实只计算一次就够了。

一个子问题的多次重复计算，耗费了大量时间。用DP处理重叠子问题，每个子问题只计算一次，从而避免了重复计算，这就是DP效率高的原因。具体的做法是首先分析得到最优子结构，然后用递推或带记忆化搜索的递归进行编程，从而实现高效的计算。

注意：DP在获得时间高效率的同时，可能耗费更多的空间，即时间效率高，空间耗费大，来动数组是优化空间效率的一个办法。（我会在后续为大家简单介绍滚动数组）

1.2 最优子结构

首先，大问题的最优解包含小问题的最优解；其次，可以通过小问题的最优解推导出大问题的最优解。这就是最优子结构。在斐波那契数列问题中，把数列的计算构造成

fib(n)=fb(n-1)+fib(n-2)

即把原来为n的大问题，减小为n-1和n-2的小问题，这是斐波那契数列的最优子结构。

在DP的概念中，还常常提到“无后效性”。简单地说，就是“未来与过去无关”。此概念不太容易理解，下面以走楼梯问题为例进行解释。要走到第n级台阶，有两种方法，一种是从第n-1级台阶走一步过来，另一种是从第n-2级台阶走两步过来。但是，前面是如何第走到第n-1级或第n-2级台阶，fib(n-1)和fib(n-2)是如何计算得到的，并不需要知道，只需要它们的计算结果就行了。换句话说，只关心前面的结果，不关心前面的过程，在计算fib(n)时，直接使用fib(n)和fib(n-1)的结果，不需要知道它们的计算过程，这就是无后效性。

无后效性是应用DP的必要条件，因为只有这样，才能降低算法的复杂度，应用DP才有意义。如果不满足无后效性，那么在计算fib(n)时，还需要重新计算fib(n-1)和fib(n-2)，算法并没有优化。

从最优子结构的概念可以看出，它是满足无后效性的。这里用斐波那契数列举例说明DP的概念，可能过于简单，不足以说明DP的特征。建议读者用后文的“0/1背包”经典问题重新理解DP的特征。

2. DP的两种编程方法

处理DP中的大问题和小问题，有两种思路：自顶向下(Top-Down，先大问题，再小问题）、自底向上(Bottom-Up，先小问题，再大问题)。

编码实现DP时，自顶向下用带记忆化搜索的递归编码，自底向上用递推编码。两种方的复杂度是一样的，每个子问题都计算一遍，而且只计算一遍。

2.1 自顶向下与记忆化

先考虑大问题，再缩小到小问题，递归很直接地体现了这种思路。为避免递归时重复计算子问题，可以在子问题得到解决时就保存结果，再次需要这个结果时，直接返回保存的结果就可以了。这种存储已经解决的子问题的结果的技术称为记忆化（Memoization）。

以斐波那契数列为例，记忆化代码如下。

int memoize[N];
int fib(int n)
{
    if(n == 1 || n == 2) return 1;
    if(memoize[n] != 0) return memoize[n];
    memoize[n] = fib(n - 1) + fib(n - 2);
    return memoize[n];
}

在这段代码中，一个斐波那契数列只计算一次，所以总复杂度为O(n)。

2.2 自底向上与制表递推

这种方法与递归的自顶向下相反，避免了用递归编程。自底向上的方法先解决子问题，再递推到大问题，通常通过填写多维表格来完成，编码时用若干for循环语句填表，根据表中的结果，逐步计算出大问题的解决方案。

用制表法计算斐波那契数列，维护一张一维表dp[ ]，记录自底向上的计算结果，更大的数是前面两个数的和，如下所示。

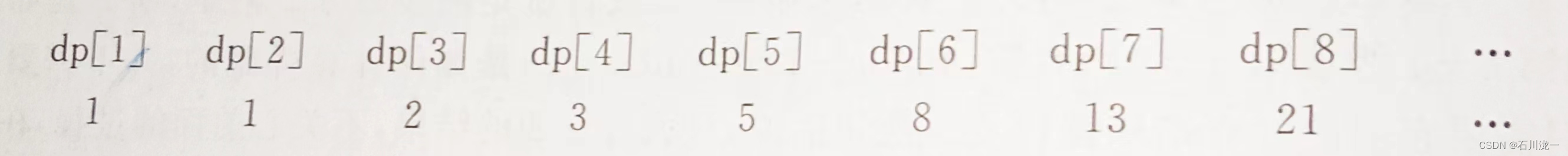
代码如下。

const int N = 255;
int dp[N];
int fib(int n)
{
    dp[1] = dp[2] = 1;
    for(int i = 3;i <= n;++i) dp[i] = dp[i-1] + dp[i-2];
    return dp[n];
}

代码的复杂度显然也为O（n）。

对比自顶向下和自底向上这两种方法，自顶向下的优点是能更宏观地把握问题、认识问题的实质；自底向上的优点是编码更直接。两种编码方法都很常见。

至此，掌握了前两节以后足以解决一些简单的DP问题，我也会在文章最后一并给出难度较低的DP例题和题解帮助大家加深印象。

3. DP的设计和实现

本节以0/1背包问题为例，详细解释与DP的设计、编程有关的内容。滚动数组也应是本节的内容，但是因为比较重要，所以后面单独用一节介绍。

背包问题在DP中很常见，其中0/1背包问题是最基础的，其他背包问题都由它衍生出来。

0/1背包问题：给定n种物品和一个背包，第i个物品的体积为ci，，价值为wi，背包的总容量为C。把物品装入背包时，第i种物品只有两种选择；装入背包或不装入背包，称为0/1背包问题。如何选择装人背包的物品，使装入背包中的物品的总价值最大?

设xi表示物品i装入背包的情况：xi=0时，不装入背包；xi=1时，装入背包。

定义：

约束条件： $\sum_{i=1}^{n} cixi\leqslant C$ ， xi=0,1

目标函数： $max\sum_{i=1}^{n}wixi$

下面给出一道0/1背包的模板题，以此题为例进行基本DP的讲解。

3.1 DP状态的设计

引入一个(N+1)×(C+1)的二维数组dp[ ][ ]，称为DP状态，dp[i][j]表示把前i个物品(从第1个到第i个)装入容量为j的背包中获得的最大价值。可以把每个dp[i][j]都看作一个背包：背包容量为j，装1~i这些物品。最后的dp[N][C]就是问题的答案——把N个物品装进容量C的背包。

3.2 DP转移方程

用自底向上的方法计算，假设现在递推到dp[i][j]，分两种情况：

(1)第i个物品的体积比容量j还大，不能装进容量j的背包。那么直接继承前i-1个物品装进容量j的背包的情况即可，即dp[i][j] = dp[i-1][j]。

(2)第i个物品的体积比容量j小，能装进背包。又可以分为两种情况：装或不装第i个物品。

1).装第i个物品。从前i-1个物品的情况推广而来，前i-1个物品的价值为dp[i-1][j]。第i个物品装进背包后，背包容量减少c[i]，价值增加w[i]，有dp[i][j] = dp[i-1][j-c[i]]+w[i]。

2).不装第i个物品，有dp[i][j]=dp[i-1][j]。

取两种情况中的最大值，状态转移方程为

dp[i][j] = max(dp[i-1][j], dp[i-1][j-c[i]]+w[i])

总结上述分析，0/1背包问题的重叠子问题是dp[i][j]，最优子结构是dp[i][j]的状态转移方程。

算法复杂度：算法需要计算二维矩阵dp[ ][ ]，二维矩阵的大小为O(NC)，每项计算时间为O(1)，总时间复杂度为O(NC)，空间复杂度为O(NC)。

0/1背包问题的简化版：一般物品具有体积(或重量)和价值两个属性，求满足体积约束条件下的最大价值。如果再简单一点，只有一个体积属性，求能放到背包的最多物品，那最后么，只要把体积看作价值，求最大体积就好了。状态转移方程变为

dp[i][j] = max(dp[i-1][j]，dp[i-1][j-c[i]]+c[i])

3.3 详解DP的转移过程

初学者可能对上面的描述仍不太清楚，下面用一个例子详细说明。有4个物品，其体积分别为(2，3，6，5)，价值分别为(6，3，5，4)，背包的容量为9。

填写dp[ ][ ]表的过程，按照只装第1个物品，只装前2个物品，只装前3个物品…的顺序，一直到装完，这就是从小问题扩展到大问题的过程。表格横向为j，纵向为i，按先横向递增j，再纵向递增i的顺序填表。dp[ ][ ]矩阵如下左图所示。

步骤1：只装第1个物品。

如由于物品1的体积为2，所以背包容量小于2的，都放不进去，即dp[1][0]=dp[1][1]=0。

若物品1的体积等于背包容量，能放进去，背包价值等于物品1的价值，即dp[1][2]=6。

容量大于2的背包，多余的容量用不到，所以价值与容量为2的背包一样，如下右图所示。

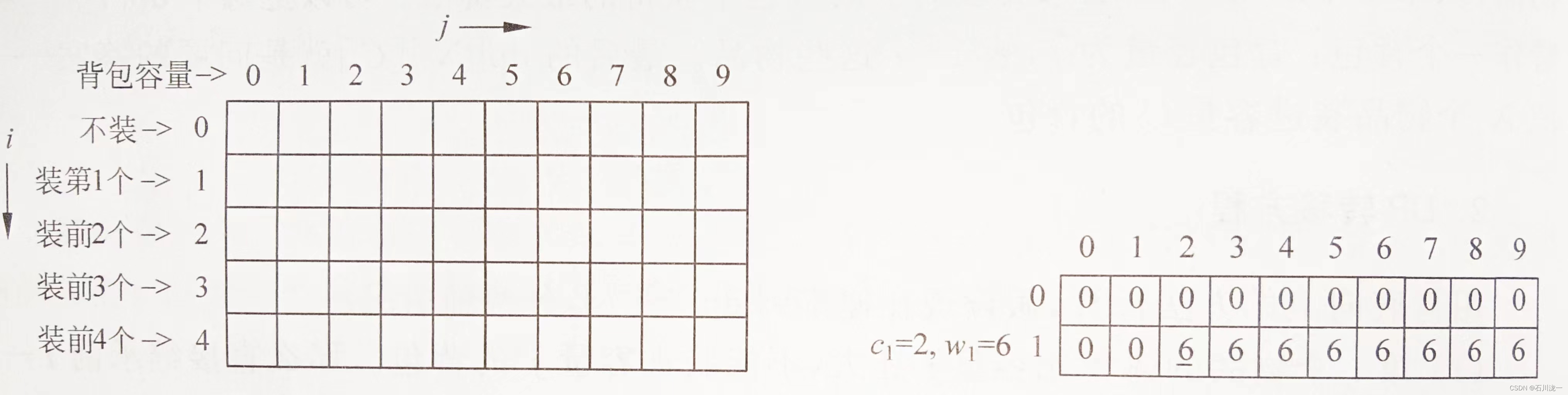
步骤2：只装前2个物品。

如果物品2体积比背包容量大，那么不能装物品2，情况与只装第1个物品一样。

dp[2][0]=dp[2][1]=0，dp[2][2]=6。

下面填写dp[2][3]。物品2体积等于背包容量，那么可以装物品2，也可以不装。

如果装物品2（体积为3，价值也为3），那么可以变成一个更小的问题，即只把物品1装到容量为j一3的背包中，如下左所示。

如果不装物品2，那么相当于只把物品1装到背包中，如下右图所示。

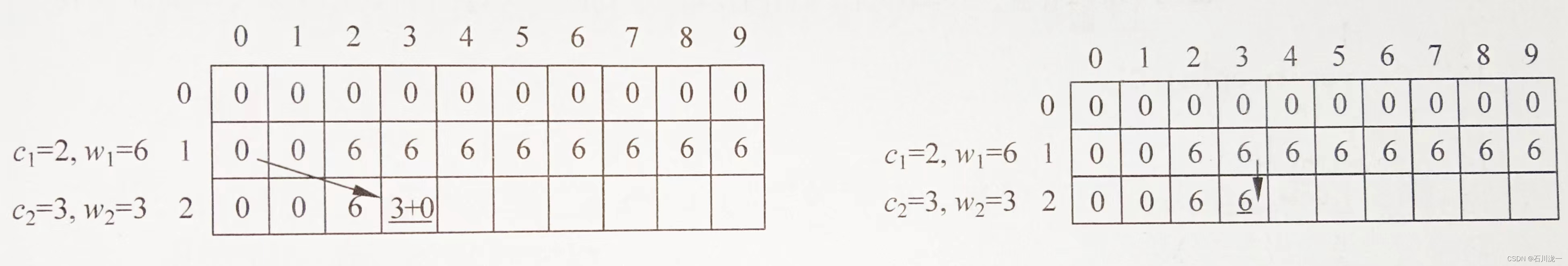
取两种情况的最大值，得dp[2][3]=max{3,6}=6。

后续步骤：继续以上过程，最后得到如下左图所示的dp矩阵（图中的箭头是几个例子)。最后的答案是dp[4][9]，把4个物品装到容量为9的背包，最大价值为11。

3.4 输出背包方案

现在回头看具体装了哪些物品。需要倒过来观察：

dp[4][9]=max{dp[3][4]+4，dp[3][9]} = dp[3][9]，说明没有装物品4，用x4=0表示；

dp[3][9]=max{dp[2][3]+5，dp[2][9]} = dp[2][3]+5 = 11，说明装了物品3，x3=1；

dp[2][3]=max{dp[1][0]+3，dp[1][3]} = dp[1][3]，说明没有装物品2，x2=0；

dp[1][3]=max{dp[0][1]+6，dp[0][3]} = dp[0][1]+6 = 6，说明装了物品1，x=1。如下右图所示，实线箭头标识了方案的转移路径。

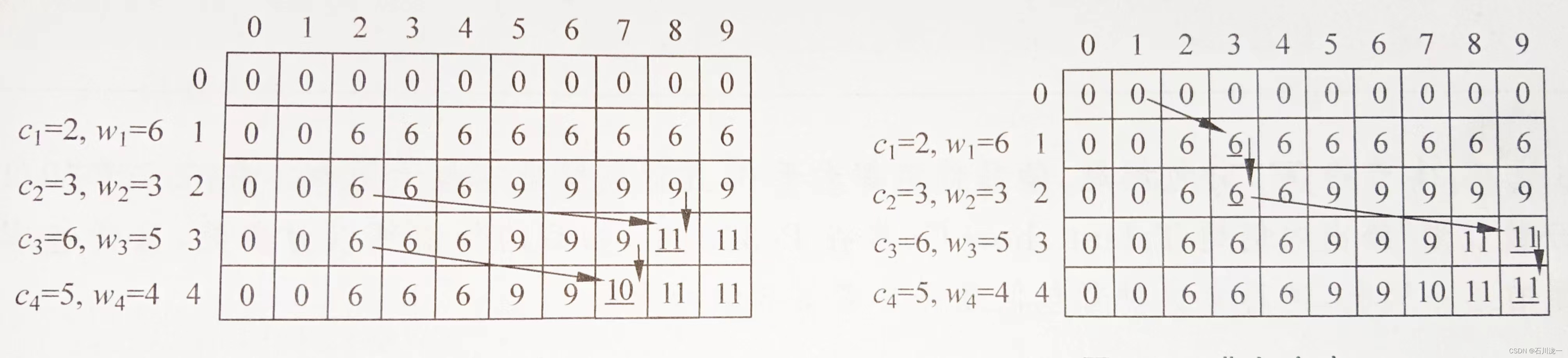
3.5 递推代码和记忆化代码

下面的代码分别用自底向上的递推和自顶向下的记忆化递归实现。

1).递推代码

#include<bits/stdc++.h>
using namespace std;
const int N = 1011;
int w[N],c[N];//物品的价值和体积
int dp[N][N];
int solve(int n,int C){
    for(int i=1;i<=n;++i){
        for(int j=0;j<=C;++j){
            if(c[i]>j) dp[i][j] = dp[i-1][j];//第i个物品比背包还大，装不了
            else dp[i][j] = max(dp[i-1][j],dp[i-1][j-c[i]]+w[i]);//第i个物品能装
        }
    }
    return dp[n][C];
}
int main(){
    int t;
    cin >> t;
    while(t--){
        cin >> n >> C;
        for(int i=1;i<=n;++i) cin >> w[i];
        for(int i=1;i<=n;++i) cin >> c[i];
        memset(dp,0,sizeof(dp));//这是初始化数组，可以对二维数组进行初始化，但局限性是由于memset是按照字节赋值，所以只能赋值为0或-1，有需要可以了解fill填充
        cout << solve(n,C) << endl;
    }
    return 0;
}

2).记忆化代码

记忆化代码只改动递推代码中的solve（）函数。

int solve(int i,int j){//前i个物品，放进容量j的背包
    if(dp[i][j] != 0) return dp[i][j];//记忆化
    if(i == 0) return 0;
    int res;
    if(c[i] > j) res = solve(i-1,j);//第i个物品比背包还大，装不了
    else res = max(solve(i-1,j),solve(i-1,j-c[i])+w[i]);//第i个物品可以装
    return dp[i][j] = res;
}

4. 滚动数组

滚动数组是DP最常使用的空间优化技术。
DP的状态方程常常是二维和二维以上，占用了太多空间。例如第3节的代码使用了二维矩阵int dp[N][C]，设N=10^3，C=10^4，都不算大，但int型占据4B，矩阵需要的空间为4×10^3×10^4 $\approx$ 40MB，已经超过一般竞赛题的空间限制。

用滚动数组可以极大减少空间。它能把二维状态方程O(n^2)的空间复杂优化到一维的O(n)，更高维的数组优化后也可以减少一维。

从状态转移方程dp[i][j] = max(dp[i-1][j]，dp[i-1][j-c[i]]+w[i])可以看出,dp[i][]只与dp[i-1][]有关，和前面的dp[i-2][],dp[i-3][]…都没有关系。从前面的图表也可以看出，每行是通过上面一行算出来的，与更前面的行没有关系。那些用过的已经无用的dp[i-2][]，dp[i-3][]，…多余了，那么干脆就复用这些空间，用新的一行覆已经无用的一行(滚动)，只需要两行就够了。下面给出滚动数组的两种实现方法，两种实现方法都很常用。

4.1 交替滚动

定义dp[2][j]，用dp[0][]和dp[1][]交替滚动。这种方法的优点是逻辑清晰，编码不出错，建议初学者采用这种方法。

下面的代码中，now始终指向正在计算的最新的一行，old指向已计算过的旧的一行。对照原递推代码，now相当于i，old相当于i-1。

int dp[2][N];//替换 dp[][]
int solve(int n,int C){
    int now = 0,old = 1;//now指向当前正在计算的一行，old指向旧的一行
    for(int i=1;i<=n;++i){
        swap(old,now);//交替滚动，now始终指向最新的一行
        for(int j=0;j<=C;++j){
            if(c[i]>j) dp[now][j] = dp[old][j];
            else dp[now][j] = max(dp[old][j],dp[old][j-c[i]]+w[i]);
        }
    }
    return dp[now][C];//返回最新的行
}

注意，j循环是0~C，其实反过来也可以。但是在下面的“自我滚动”代码中，必须反过来循环，即C~0。

4.2 自我滚动

用两行做交替滚动在逻辑上很清晰，但是还能继续精简：一维dp就够了，自己滚动自己。

int dp[N];
int solve(int n,int C){
    for(int i=1;i<=n;++i){
        for(int j=C;j>=c[i];--j){
            dp[j] = max(dp[j],dp[j-c[i]]+w[i]);
        }
    }
    return dp[C];
}

注意，j应该反过来循环，即从后向前覆盖。下面说明原因，用dp[j]’表示旧状态，dp[j]表示滚动后的新状态。

1). j从小到大循环是错误的。例如，i=2时，下图左侧的dp[5]，经计算得到dp[5]=9，把dp[5]更新为9。继续计算，当计算dp[8]时，得dp[8]=dp[5]’+3=9+3=12，这个答案是错的。错误的产生是由动数组重复使用同一个空间引起的。

2). j从大到小循环是对的。例如，i=2时，首先计算最后的dp[9]=9，它不影响前面状态的计算，如下图所示。

经过交替滚动或自我滚动的优化，DP的空间复杂度从O(NXC)降低到O(C)。

滚动数组也有缺点。它覆盖了中间转移状态，只留下了最后的状态，所以损失了很多信息，导致无法输出具体的方案。

二维以上的dp数组也能优化。例如，求dp[t][ ][ ]，如果它只和dp[t-1][ ][ ]有关，不需要dp[t-2][ ][ ]、dp[t-3][ ][ ]等，那么可以把数组缩小为dp[2][ ][ ]或dp[ ][ ]。

5.题目示例

下面以一道难度较低的DP蓝桥真题帮助大家联系。

对DP不太熟练的可以在这里停留思考一下，下面直接上代码。

#include<bits/stdc++.h>
using namespace std;
int sum={};
void count_coin(int a[],int n,int k,int m)
{
    if(k==0){
        sum++;//如果k=0，说明当前这种组合方式可以凑出指定的数额
    }else{
        for(int j=0;j<n;++j){//反之对每一个面值的硬币都进行下一步判断
            if(k>=a[j] && a[j]>=m-k) count_coin(a,n,k-a[j],k);//大于零是一个重要的判断条件，如果丢失这个条件可能会导致无限递归调用，类似的题目中也应注意条件的控制
        }
    }
}
int main()
{
    int n,k;
    cin >> n >> k;
    int num[n];
    for(int i=0;i<n;++i){
        cin >> num[i];
    }sort(num,num+n);//这里对硬币面值进行非递减排序，是为了某些特殊情况可以直接判断
    if(k<num[0]) goto ending;//若要凑出的数额小于面值最小的硬币，那么一定无法凑出k，直接跳过判断
    count_coin(num,n,k,k);
    ending:
      cout << sum << endl;
    return 0;
}

这道题相对简单，可以轻松掌握的可以到官网自行练习高难度的DP。

以上就是DP概念和编程方法的全部内容，如有纰漏之处，欢迎各位指正批评，后续我会继续更新动态规划一章的内容，希望可以帮助到大家。