双指针思想的应用：15. 三数之和 & 18. 四数之和

三数之和

题目链接：15. 三数之和 - 力扣（LeetCode）

参考视频：梦破碎的地方！| LeetCode：15.三数之和_哔哩哔哩_bilibili

---

关键难点：答案中不可以包含重复的三元组。

这种情况下，先前在四数相加中使用的哈希表的解题思路并不完全适用于此题，去重操作大大提升了此问题的时间复杂度

此时，考虑到采用双指针思想（老实说，个人不太懂为啥就能想到能用这种方法，还需要多学习），此种方法易于理解

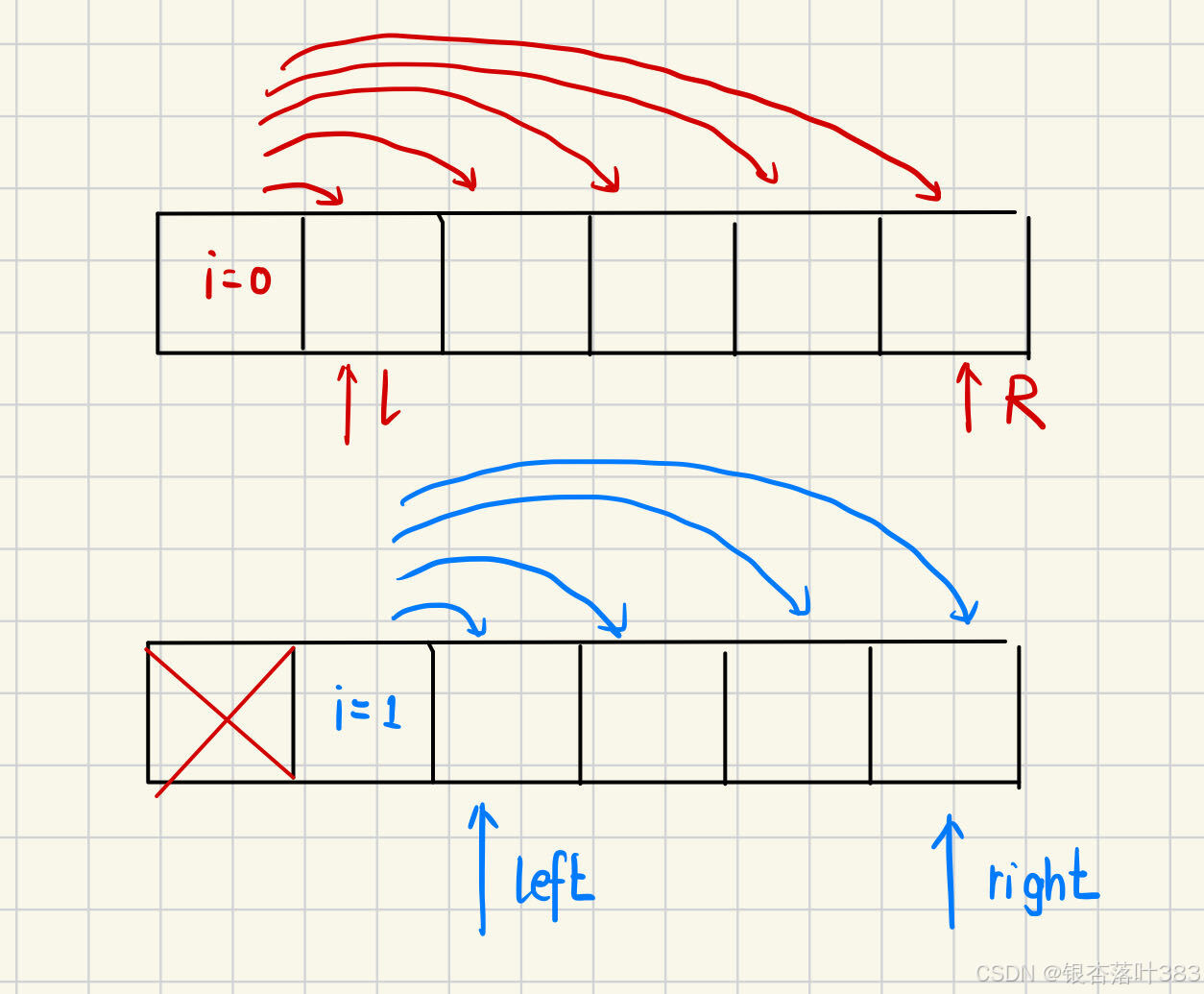
具体思路

（1）先对数组进行从小到大的排序，再开始遍历元素

（2）i从下标0的地方开始，同时定一个下标left 定义在i+1的位置上，定义下标right 在数组结尾的位置上。只要在两个指针找到i位置对应元素数值的相反数即可（给出了目标值，这一下就变成了类似两数相加的问题了，实际问题不同，但思想上类似）

（3）移动双指针（此时为从小到大的排序）

    如果nums[i] + nums[left] + nums[right] > 0 就说明 此时三数之和大了，因为数组是排序后了，   所以right下标就应该向左移动，这样才能让三数之和小一些。

    如果 nums[i] + nums[left] + nums[right] < 0 说明 此时三数之和小了，left 就向右移动，才能让  三数之和大一些，直到left与right相遇为止。

关键要点：去重操作

（1）对遍历元素的去重：

 判断 nums[i] 与 nums[i - 1] 是否相同。

为什么要判断 nums[i] 与 nums[i - 1] 是否相同？

如果我们判断 nums[i] 与 nums[i + 1] 是否相同，当遍历到第一个 -1 时，由于下一个也是 -1，这组数据就会被跳过。而我们需要确保三元组内的元素可以重复，但三元组整体不能重复。

正确写法保证了当前使用 nums[i]，只要前一位没有相同的元素，{-1, -1, 2} 这样的数据可以被收录到结果集中。而如果前位有相同的数据的话，那么该次结果就已经在上一位元素检索时被包含进去了，因此可以不收录

if (i > 0 && nums[i] == nums[i - 1]) {
                continue;
            }
            int left = i + 1;
            int right = nums.size() - 1;

（2）对左右指针的去重

 while (left < right && nums[left] == nums[left - 1]) left++;

这个逻辑的目的是，当 nums[left] 与 nums[left + 1] 相同时，我们继续将 left 向右移动，直到找到一个与 nums[left] 不同的元素或者 left 超过 right。这样可以确保在下一次循环中，不会再次使用与当前 nums[left] 相同的元素，避免生成重复的三元组。（右指针亦同理）

---

四数之和

关键要点：

与上题的区别在于剪枝操作有了更加严格的要求，其他大体思路不变[在原来的基础上加了一层遍历]——》target不定，因此只有target>0,k值（最外层遍历元素）>0,k>target的情况下才能进行剪枝操作。