编译原理复习---SSA

适用于电子科技大学编译原理期末考试复习。

1. SSA的概念

SSA（Static Single Assignment），即静态单赋值，是一种在编译过程中使用的中间表示形式，它要求每个变量在其生命周期内只被赋值一次。这种形式简化了编译器的分析和优化过程，使得数据流分析和优化算法变得更加简单和高效。

SSA的核心概念

1. 唯一赋值：在SSA形式中，每个变量只被赋值一次。如果一个变量在原始代码中被多次赋值，则在转换为SSA形式时，每次赋值都会创建一个新变量。例如，原始代码中的变量x可能在SSA形式中被转换为x1, x2, x3等。

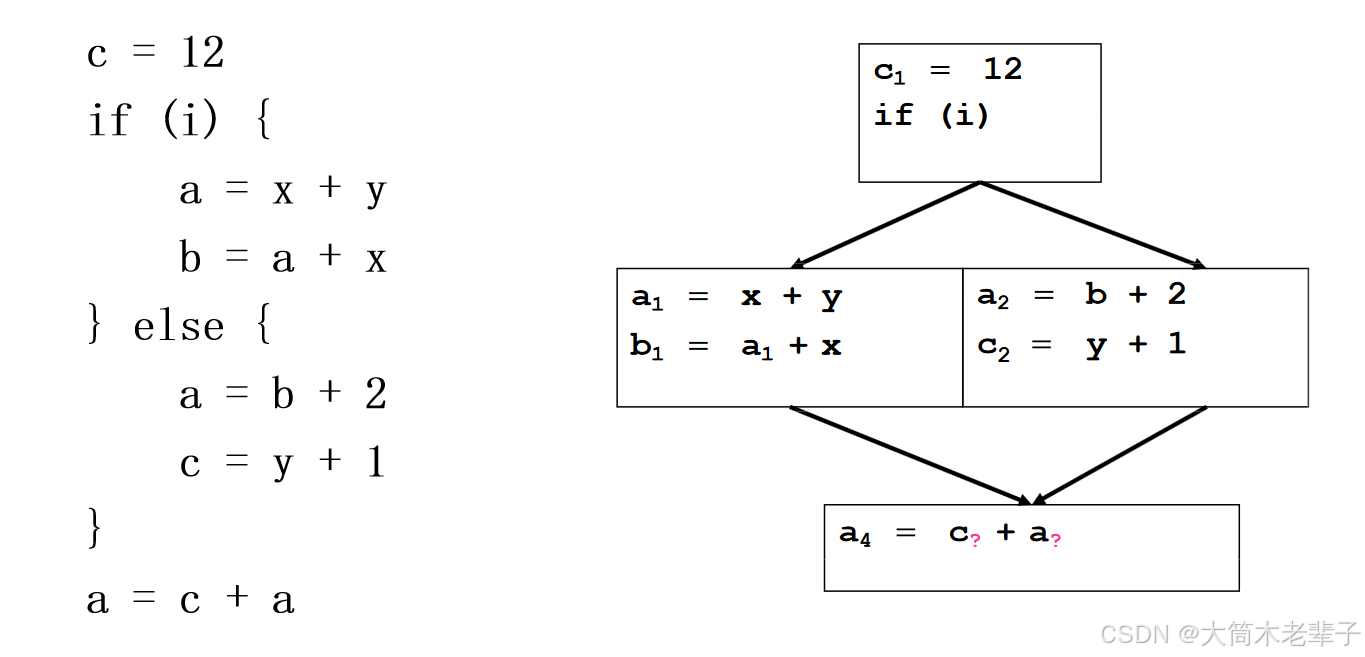
2. Φ函数：在控制流图（CFG）中，当有多个控制流路径合并时，需要引入Φ（phi）函数来选择来自不同路径的变量值。Φ函数的形式是x = Φ(x1, x2,...)，表示变量x的值根据来自不同路径的变量x1, x2, …进行选择。

 2. Φ函数

Φ函数的实现方式很简单：

本章要研究的核心问题在于，Φ函数应该在哪里插入。

2.1 支配边界

1. 支配(dom)：详见文章编译原理复习---中间代码优化-优快云博客

2. 严格支配(sdom)：x 支配 w，但 x 不是 w （即dom集排除自身）

3. 支配边界(DF)：x 支配 w 的某个前驱结点，但 x 不严格支配 w

 支配边界算法：

simpleDominanceFrontiers(Gf, dom ){
    DomBy(X) ← { Z | X ∈ dom(Z) }
    foreach X ∈ Nf do                      // 对图中每个结点 X
      foreach Y ∈ DomBy(X) do              // 对 X 支配的每个结点 Y
        foreach Z ∈ Succ(Y) do             // 对 Y 的每个后继结点 Z
           if !(Z ∈ DomBy(X) − { X })      // 如果 Z 不被 X 支配
           then DF(X) ← DF(X) ∪ { Z }      // 则将 Z 加到 X 的支配边界中
}

2.2 Φ函数插入算法

1. 某个 n 结点定义了变量 x。

2. DF(n)中的结点需要插入对应的Φ函数(插过的不重复插)。

3. 新插入了Φ函数的结点也视为定义了 x 的结点。

以伪代码形式给出：

1. orig[n]：结点 n 中定义的变量的集合。

2. defsites[v]：定义了变量 v 的结点的集合。

3. W：需要进行Φ函数插入的集合。

4. PHI[v]：插入了变量 v 的Φ函数的集合。

foreach node n {
    foreach variable v defined in n {  
        orig[n] ∪= {v}
        defsites[v] ∪= {n}
    }
}

foreach variable v {  
    W = defsites[v]  
    while W not empty {
    n = remove node from W    
    foreach y in DF[n]
        if y ∉ PHI[v] {
            insert “v = Φ(v,v,…)” at top of y  
            PHI[v] = PHI[v]∪{y}
            if v ∉ orig[y]: 
                W = W ∪ {y}
        }
    }
}