太原理工大学第七届新生赛（同步赛）

已于 2025-01-30 17:15:38 修改
阅读量343 收藏 5
点赞数 7
CC 4.0 BY-SA版权
文章标签： c++ 数据结构 算法 贪心算法 哈希算法 迭代加深
于 2025-01-26 23:12:51 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/2302_80195998/article/details/145366957

喵，12.21写的题目让我来补下错题，当时期末周好忙。

A.树

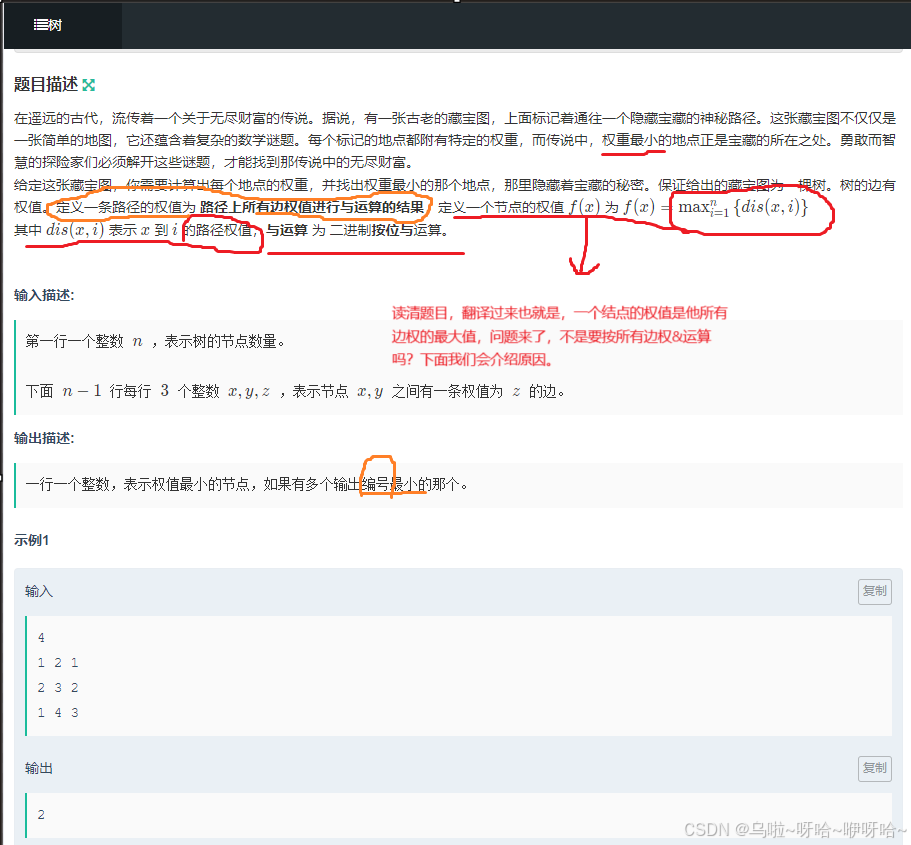
答案代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	ll n;cin>>n;
	vector<vector<pair<ll,ll>> >mp(n+1);
	for(ll i=1;i<=n-1;i++){
		ll x,y,z;cin>>x>>y>>z;
		mp[x].push_back({y,z});
		mp[y].push_back({x,z});
	}
	vector<ll> res(n+1,0);
	for(ll i=1;i<=n;i++){
		ll x=i;
		for(ll j=0;j<mp[x].size();j++){
			res[x]=max(mp[x][j].second,res[x]);
		}
	}
	ll ans=LLONG_MAX;
	ll idx=0;
	for(ll i=1;i<res.size();i++){//注意不要越界了，res.size()==n+1,写i<=res.size()会越界
		if(res[i]<ans){
			ans=res[i];
			idx=i;
		}
	}
	cout<<idx;
	return 0;
}
#include<bits/stdc++.h>
using namespace std;
int dis[1200000];
int main()
{
    int n;
    cin>>n;
    int h=n-1;
    while(h--)
    {
        int x,y,z;
        cin>>x>>y>>z;
        dis[x]=max(dis[x],z);
        dis[y]=max(dis[y],z);
    }
    int ans=1;
    for(int t=1;t<=n;t++)
        if(dis[ans]>dis[t]) ans=t;
    cout<<ans;
}

其实题目已经告诉我们答案了，只是又多说了&运算，可能对做题过程中造成一定困扰，下面让我们来具体解释一下。  

B.什么是好数组 

 

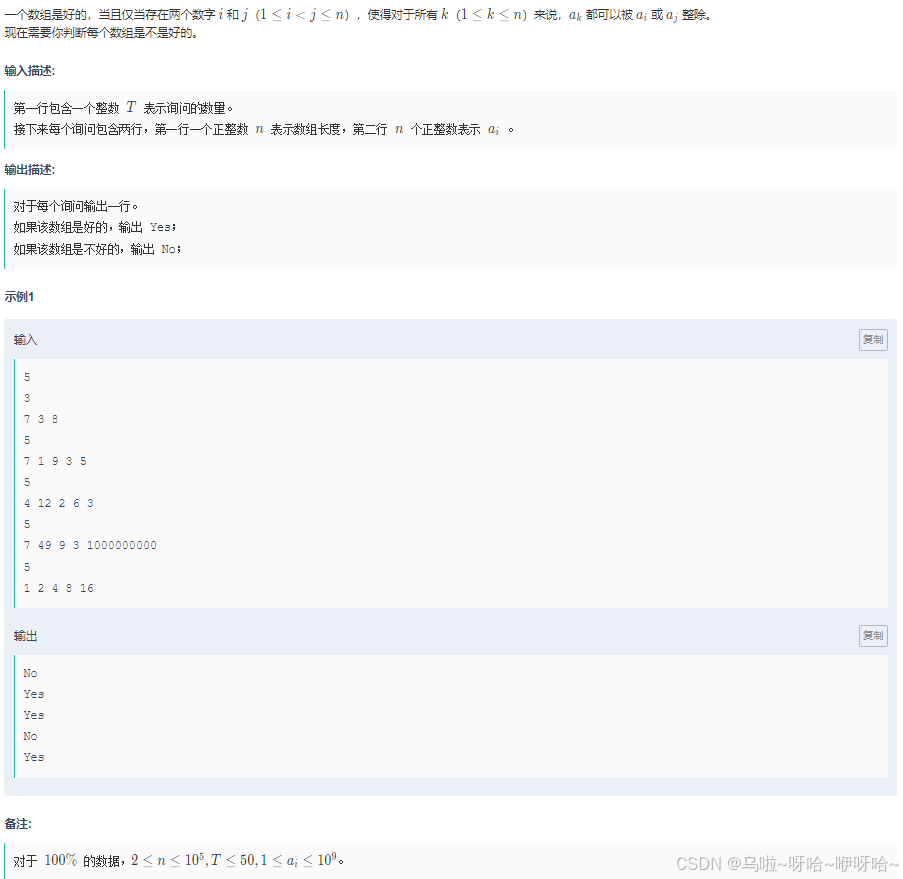
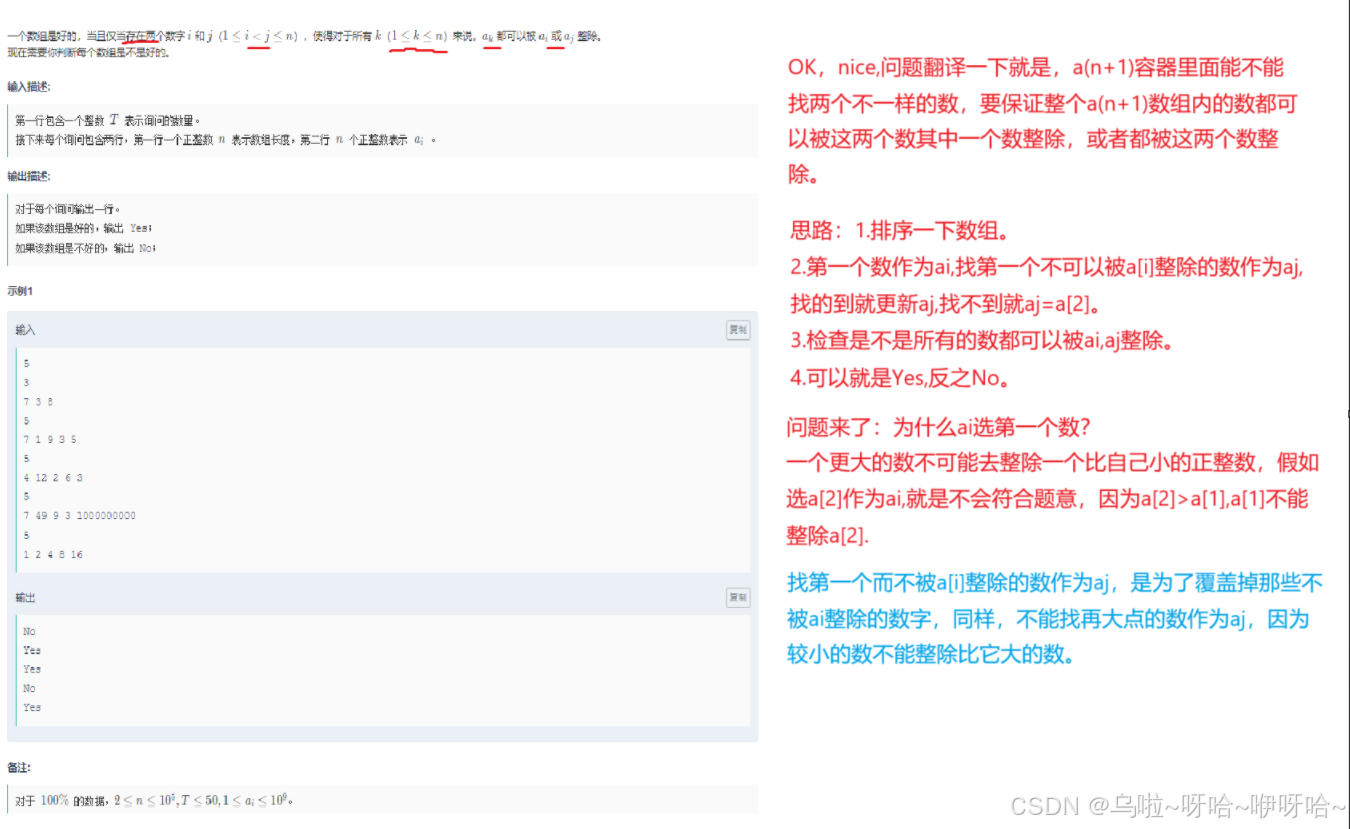
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);//要加上，不然会超时
	ll t;cin>>t;
	while(t--){
		ll n;cin>>n;
		vector<ll> a(n+1,0);
		for(ll i=1;i<=n;i++)cin>>a[i];
		if(n==2){
			cout<<"Yes"<<endl;
		}else{
			sort(a.begin(),a.end());
			ll ai=a[1],aj=-1;
			for(ll i=2;i<=n;i++){
				if(a[i]%ai!=0){
					aj=a[i];
					break;
				}
			}
			if(aj==-1)aj=a[2];
			ll flag=0;
			for(ll i=1;i<=n;i++){
				if(a[i]%ai!=0&&a[i]%aj!=0){
					flag=1;
					break;
				}
			}
			if(flag==0)cout<<"Yes"<<endl;
			else cout<<"No"<<endl;
		}
	}
	return 0;
}

C.快来帮芙芙吧* I 

 

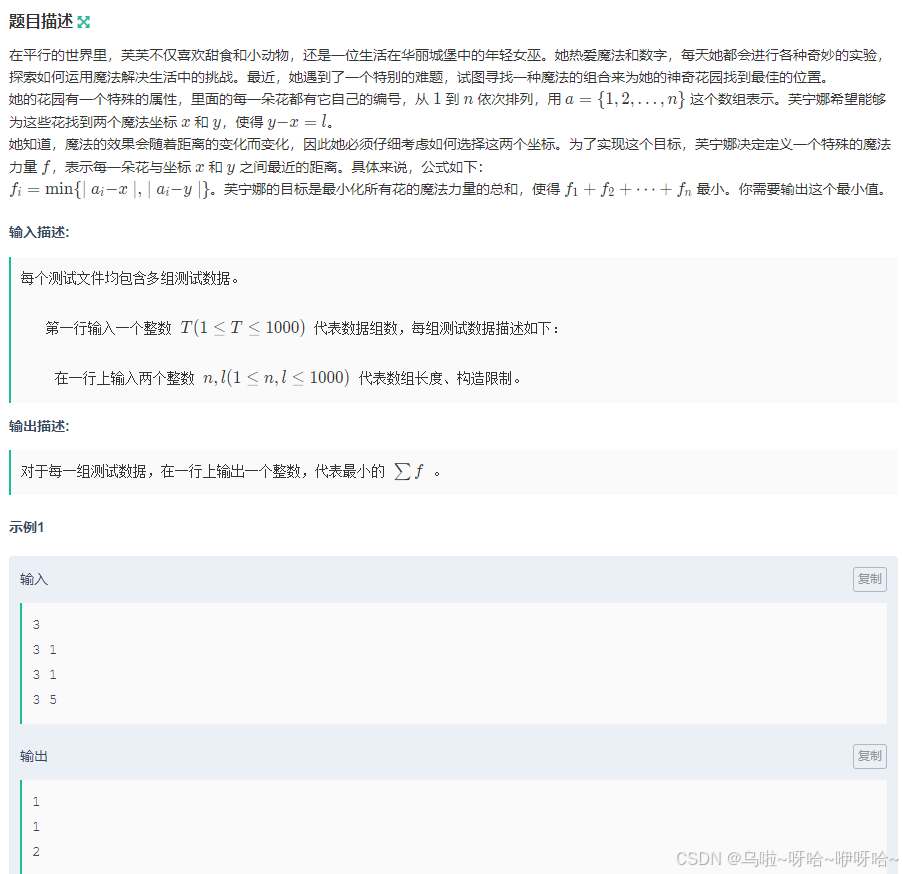
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	ll t;cin>>t;
	while(t--){
		ll n,l;cin>>n>>l;
		ll min_sum=LLONG_MAX;
		for(ll x=1-l;x<=n;x++){
			ll flag=0;
			ll current_sum=0;
			for(ll i=1;i<=n;i++){
				current_sum+=min(abs(i-x),abs(i-x-l));
				if(current_sum>=min_sum){
					flag=1;
					break;
				}
			}
			if(flag==0){
				if(current_sum<min_sum){
					min_sum=current_sum;
				}
			}
		}
		cout<<min_sum<<endl;
	}
	return 0;
}

D.快来帮芙芙吧* II 

 

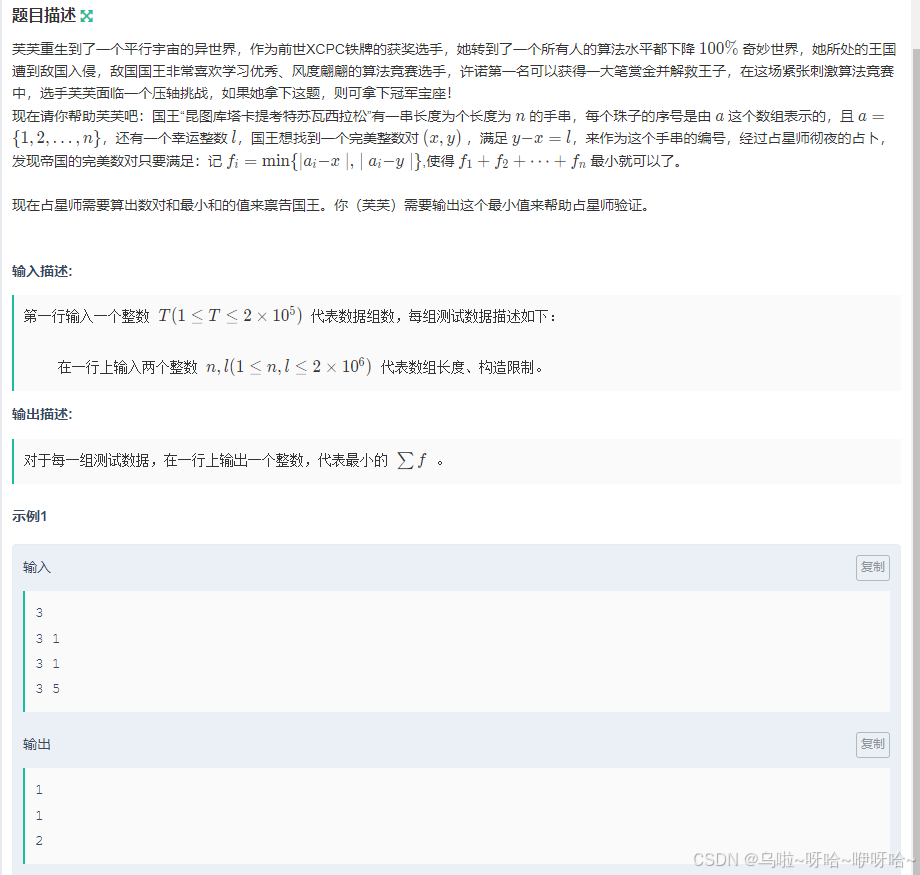
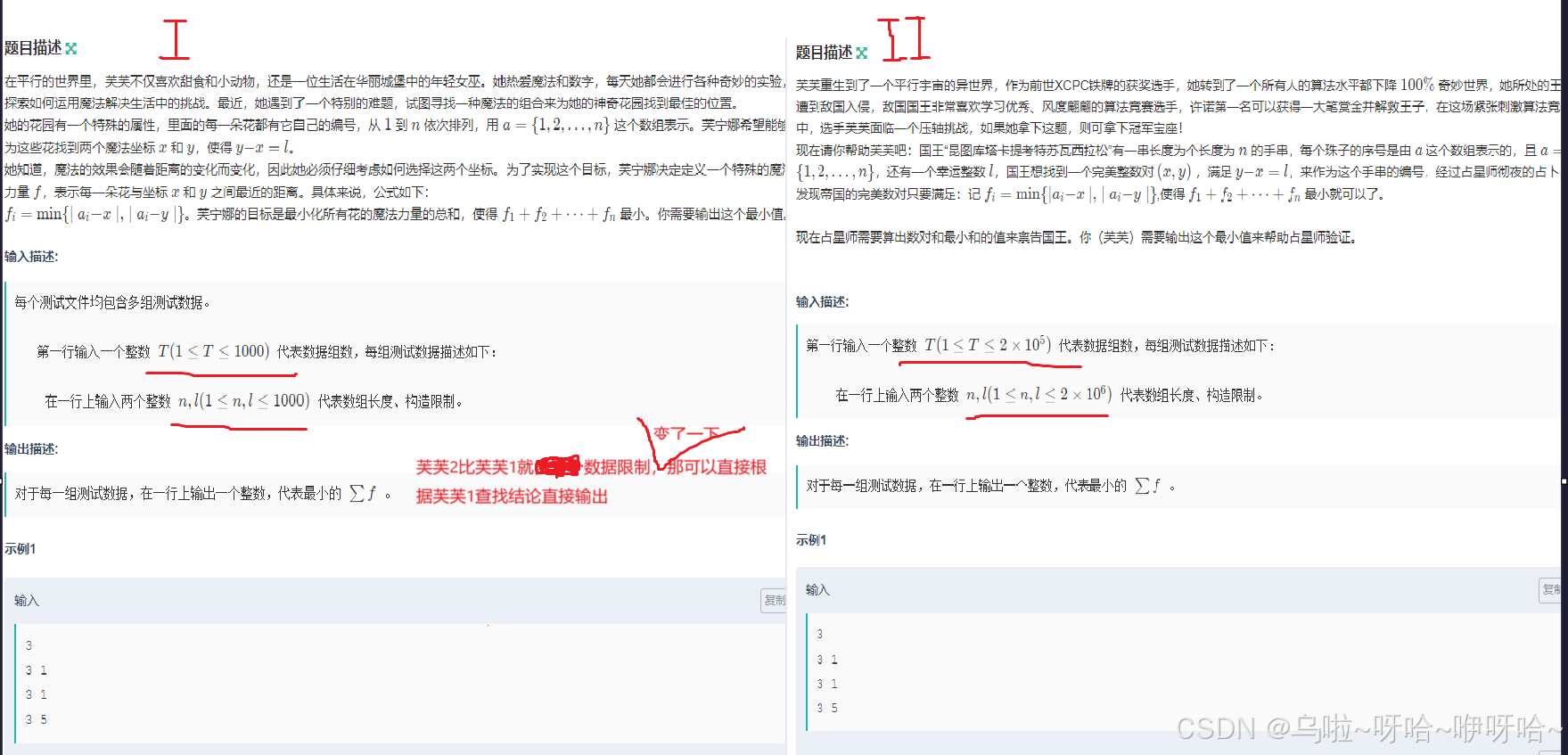
下面开始数据模拟，四种情况每样一个。 

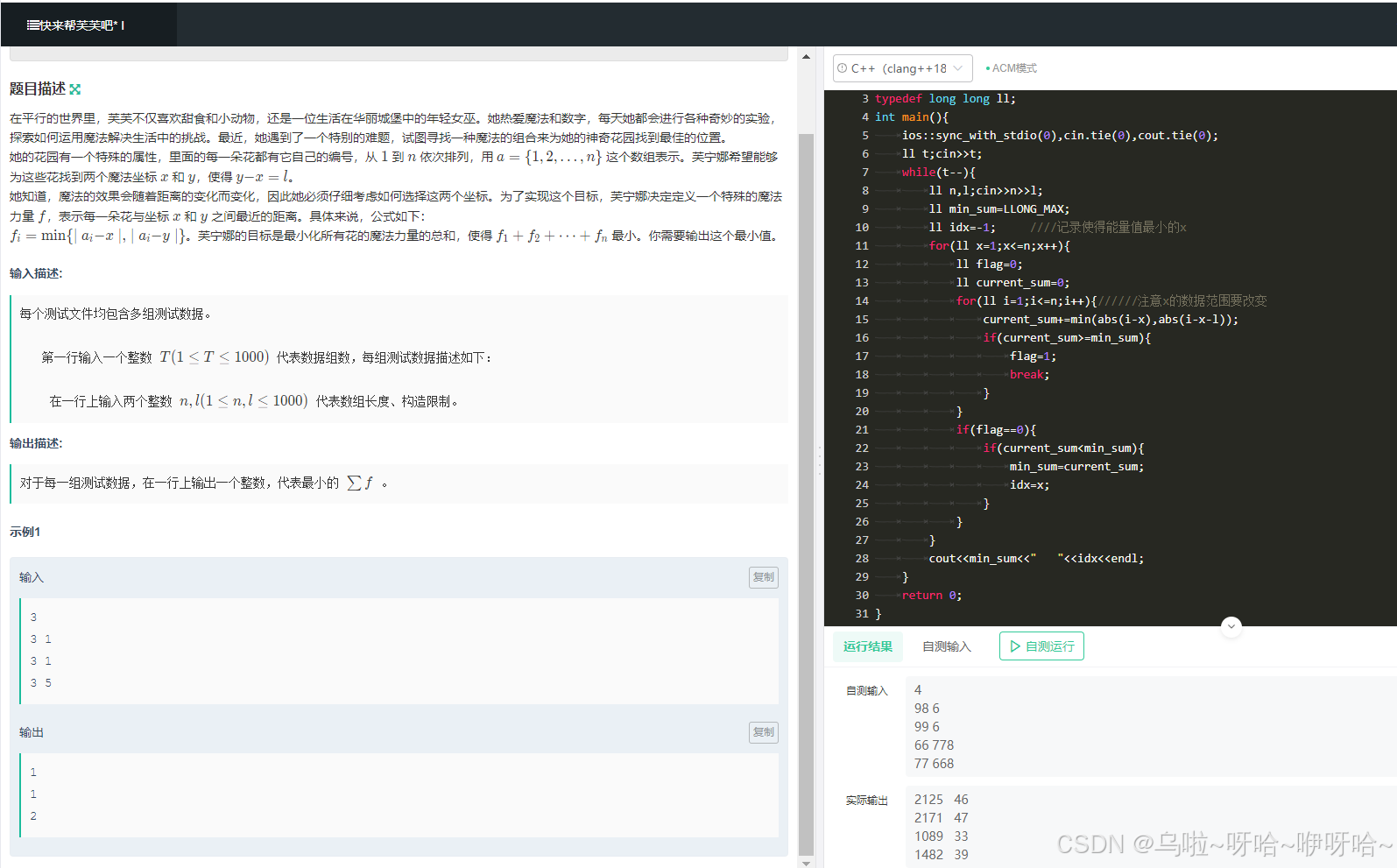
模拟数据的芙芙1代码： 

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	ll t;cin>>t;
	while(t--){
		ll n,l;cin>>n>>l;
		ll min_sum=LLONG_MAX;
		ll idx=-1;     /////
		for(ll x=1;x<=n;x++){     ////注意范围
			ll flag=0;
			ll current_sum=0;
			for(ll i=1;i<=n;i++){
				current_sum+=min(abs(i-x),abs(i-x-l));
				if(current_sum>=min_sum){
					flag=1;
					break;
				}
			}
			if(flag==0){
				if(current_sum<min_sum){
					min_sum=current_sum;
					idx=x;
				}
			}
		}
		cout<<min_sum<<"   "<<idx<<endl;
	}
	return 0;
}

 此时也就后两种情况的规律比较容易看出来，现在来验证后两种规律是否正确。

/*
  根据数据模拟发现规律
  <1>  if(n>l && n%2==0)
       x=
  
  <2>  if(n>l && n%2!=0)
       x=
  
  <3>  if(l>n && n%2==0)
       x=n/2
  
  <4>  if(l>n && n%2!=0)
       x=n/2+1
 */

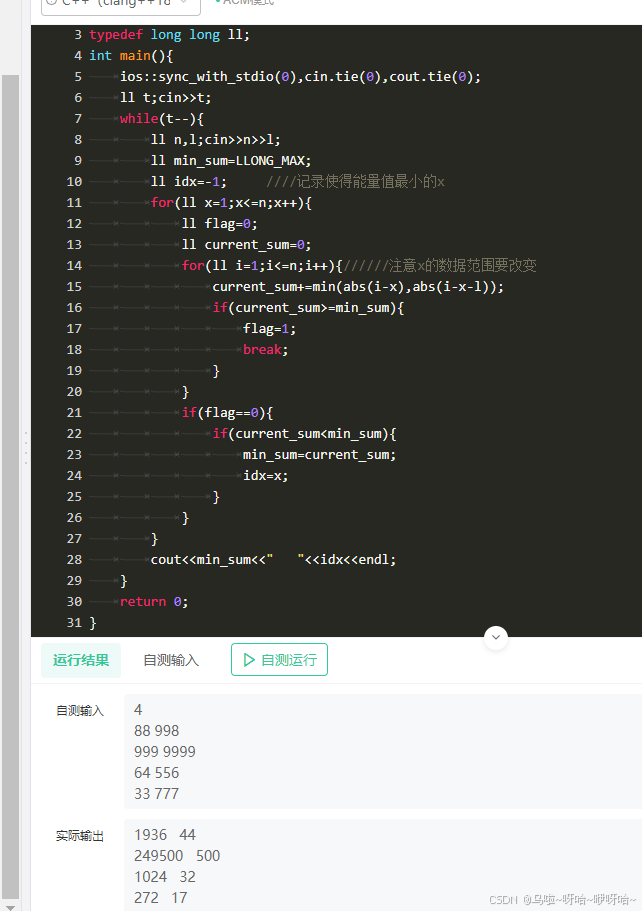
OK ，nice 现在找前两种规律 。

 

/*
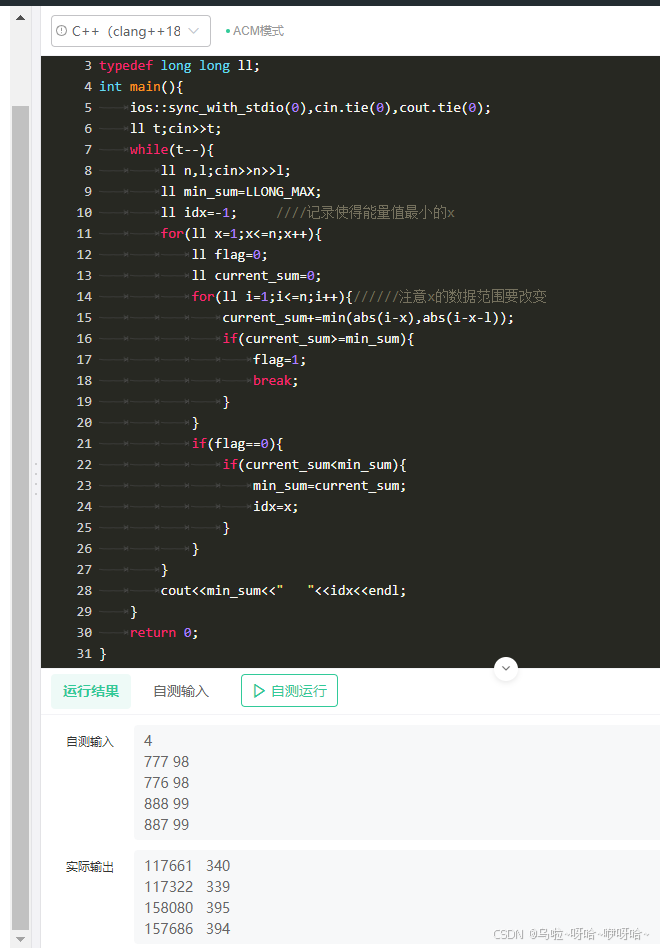
  根据数据模拟发现规律
  <1>  if(n>l && n%2==0)
       x=(n-l+1)/2
  
  <2>  if(n>l && n%2!=0)
       x=(n-l+1)/2
  
  <3>  if(l>n && n%2==0)
       x=n/2
  
  <4>  if(l>n && n%2!=0)
       x=n/2+1
 */

 OK ，nice 直接把规律输出，时间复杂度O(n)。

​
#include <bits/stdc++.h>
#define int long long
using namespace std;
int t;
int n,l;
signed main()
{
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    cin>>t;
    int x,y;
    while(t--){
        cin>>n>>l;
        if(l>=n){
            if(n%2){
                x=(n+1)/2;
                y=x+l;
            }
            else{
                x=n/2;
                y=x+l;
            }
        }
        else{
            x=(n-l+1)/2;
            y=x+l;
        }
        int sum=0;
        for(int j=1;j<=n;j++){
            sum+=min(abs(j-x),abs(y-j));
        }
        cout<<sum<<'\n';
    }
    return 0;
}


​

E. BF* I

 

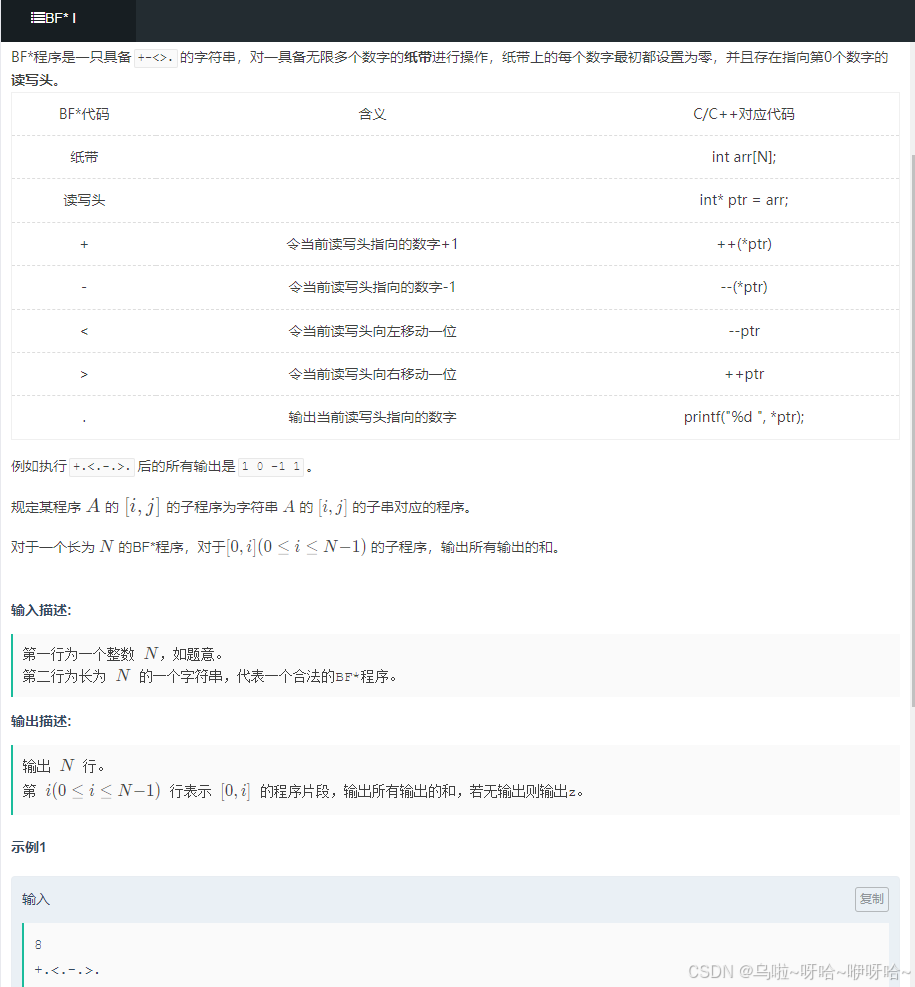
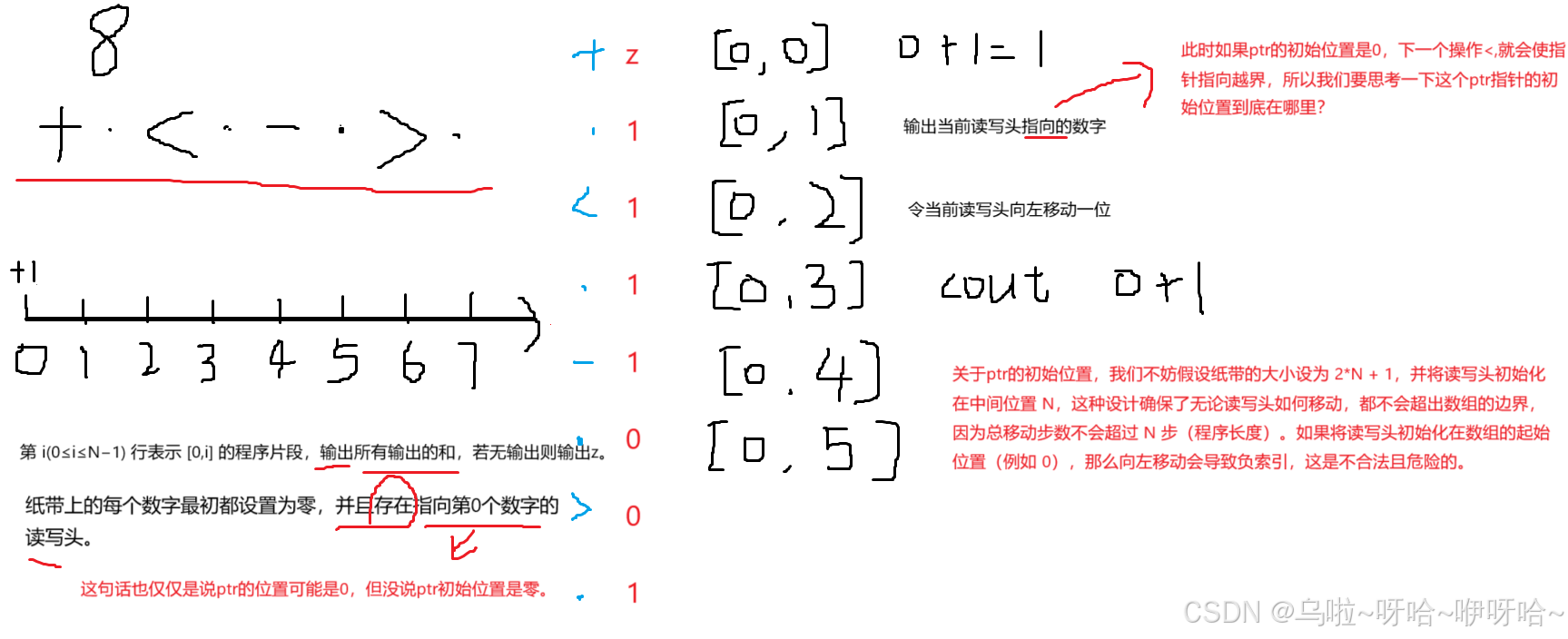
逆天代码竟然超时了，不过有知道了一个细节，我只能说，不积跬步无以至千里，不积小流无以成江河。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=1e6;
int main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	ll n;cin>>n;
	string s;cin>>s;
	vector<ll> a(2*N+5,0);
	ll ptr=N;
	ll cur_sum=0;
    ll flag=0;
	for(ll i=0;i<n;i++){
		if(s[i]=='.'){
			cur_sum+=a[ptr];
			flag=1;
		}
		else if(s[i]=='+')a[ptr]++;
		else if(s[i]=='-')a[ptr]--;
		else if(s[i]=='<')ptr--;
		else if(s[i]=='>')ptr++;
		if(flag==1)cout<<cur_sum<<endl;
		else cout<<'z'<<endl;
	}
	return 0;
}

正确代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll N=1e6;
int main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	ll n;cin>>n;
	string s;cin>>s;
	vector<ll> a(2*N+5,0);
	ll ptr=N;
	ll cur_sum=0;
    ll flag=0;
	for(ll i=0;i<n;i++){
		if(s[i]=='.'){
			cur_sum+=a[ptr];
			flag=1;
		}
		else if(s[i]=='+')a[ptr]++;
		else if(s[i]=='-')a[ptr]--;
		else if(s[i]=='<')ptr--;
		else if(s[i]=='>')ptr++;
		if(flag==1)cout<<cur_sum<<'\n';
		else cout<<'z'<<'\n';
	}
	return 0;
}

 

F.average 

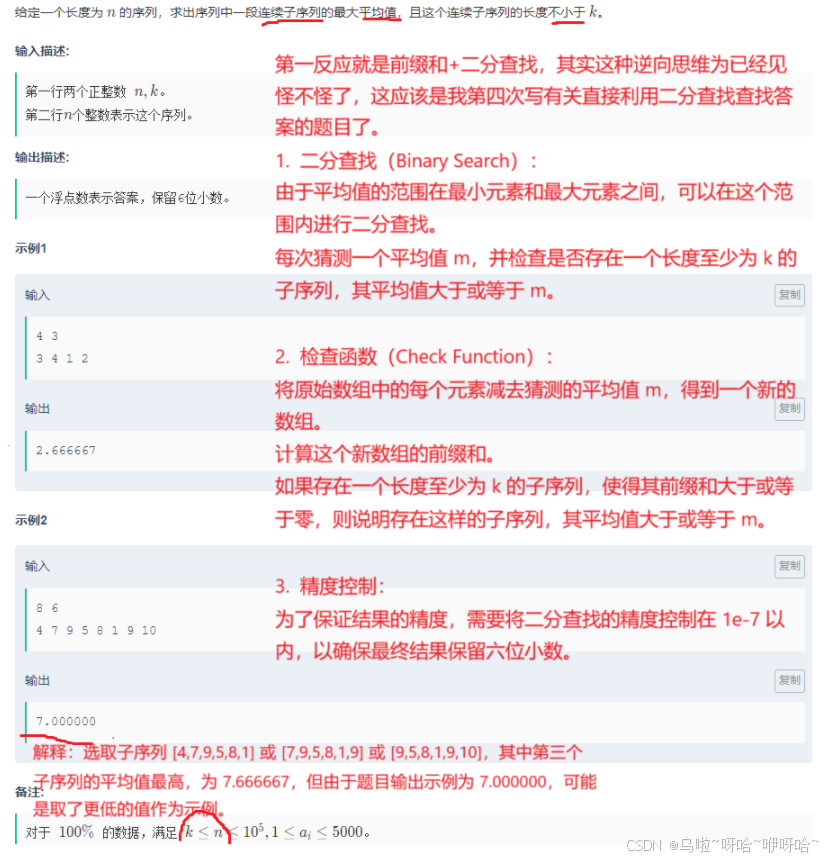
#include<bits/stdc++.h>
using namespace std;
typedef double ll;
ll n,k;
bool check(ll mid,vector<ll> &s,vector<ll> &a){
	for(ll i=1;i<=n;i++){
		s[i]=s[i-1]+(a[i]-mid);
	}
	ll xiao_v=1e17;
	for(ll i=k;i<=n;i++){
		xiao_v=min(xiao_v,s[i-k]);
		if(s[i]-xiao_v>=0)return true;
	}
	return false;
}
int main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>k;
	vector<ll> a(n+1,0);
	vector<ll> s(n+1,0);
	ll MIN=-1e17,MAX=1e17;
	for(ll i=1;i<=n;i++){
		cin>>a[i];
		MIN=min(MIN,a[i]);
		MAX=max(MAX,a[i]);
	}
	ll l=MIN,r=MAX;
	ll mid=0;
	while(r-l>1e-6){
		mid=(r+l)/2;
		if(check(mid,s,a)){
			l=mid;
		}else r=mid;
	}
	cout<<fixed<<setprecision(6)<<l<<'\n';
	return 0;
}
​
#include<bits/stdc++.h>
using namespace std;
#define int long long
double a[120000],s[120000];
int n,k;
int check(double x)
{
    for(int t=1;t<=n;t++) s[t]=s[t-1]+a[t]-x;
    double v=1e17;
    for(int t=k;t<=n;t++)
    {
        v=min(v,s[t-k]);
        if(s[t]-v>=0) return 1;
    }
    return 0;
}
 
 
signed main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
     
    cin>>n>>k;
    for(int t=1;t<=n;t++) cin>>a[t];
    double l=0,r=5000;
    while(r-l>1e-6)
    {
        double mid=(l+r)/2;
        if(check(mid)) l=mid;
        else r=mid;
    }
    printf("%.6lf",l);
}

​

 

 

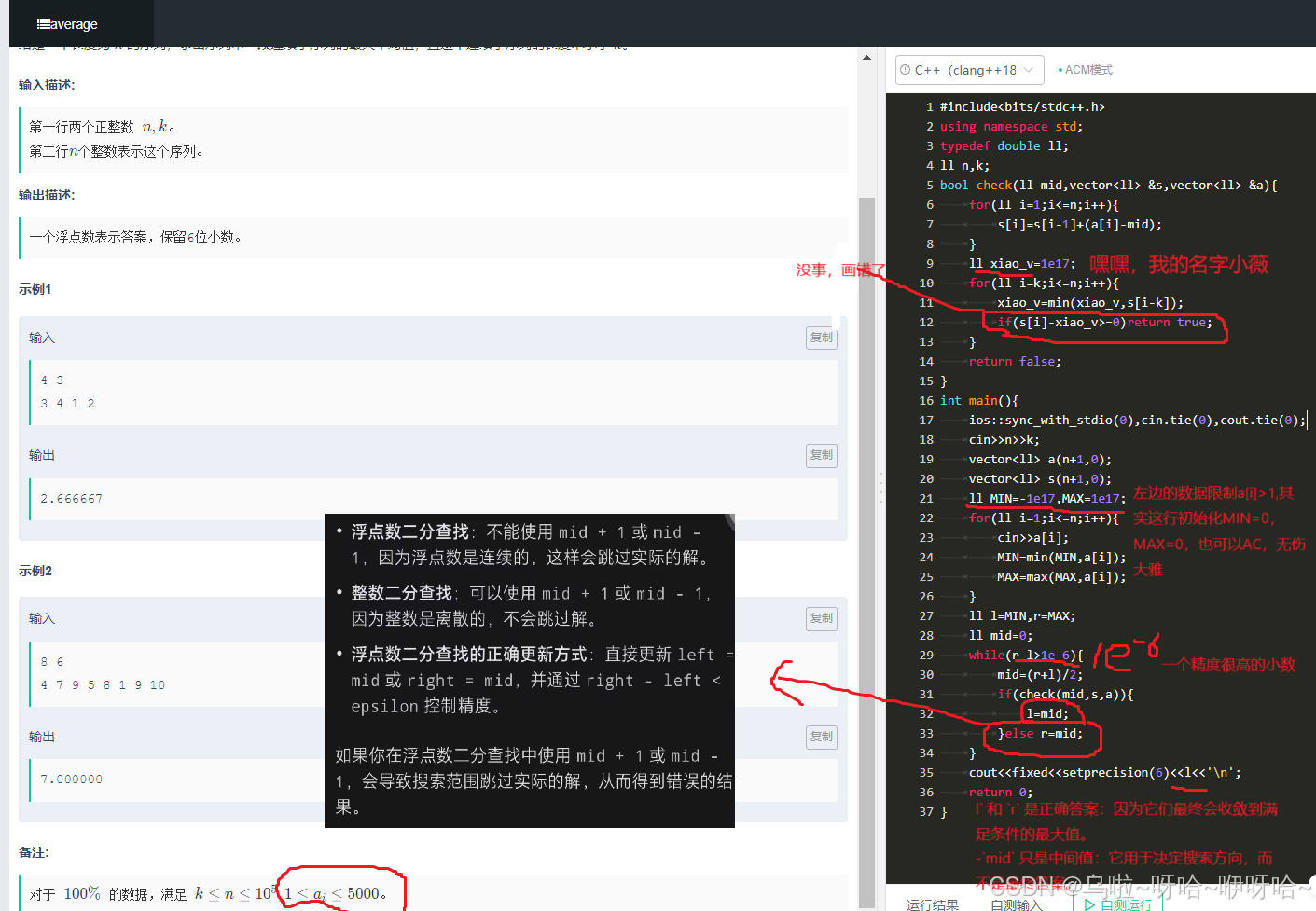
为什么不需要单独检查更长的子序列？

当我们遍历到位置 i并更新 xiao_v，实际上已经隐含地检查了所有长度从 k 到 i 的子序列。具体原因如下：

  • 任意长度 ≥ k的子序列 都可以被分解为至少一个长度为 k 的子序列加上额外的元素。因此，只要存在一个长度为 k的子序列满足条件，或更长的子序列通过包含长度为 k 的子序列来满足条件，s[i] - xiao_v>= 0 就会捕捉到这一点。
  • 维护 xiao_v确保我们考虑了所有可能的起始位置 j≤i−k，覆盖了所有长度至少为 k的子序列。

具体示例解析

让我们通过具体的例子来更好地理解这一点。

 

G.操作 

 

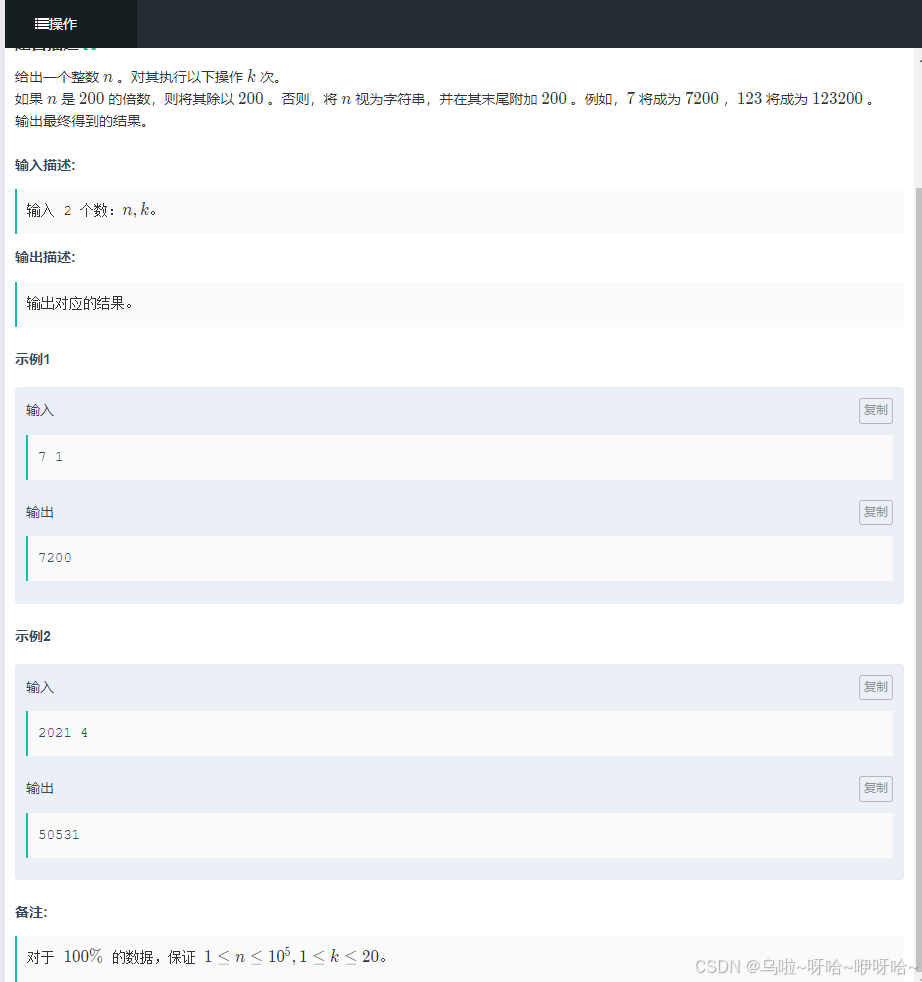
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main() {
    ll n, k;
    cin >> n >> k;
    while (k--) {
        if (n % 200 == 0) {
            n /= 200;
        } else {
            n = stoll(to_string(n) + "200");
        }
    }
    cout << n << endl;
    return 0;
}

H.path 

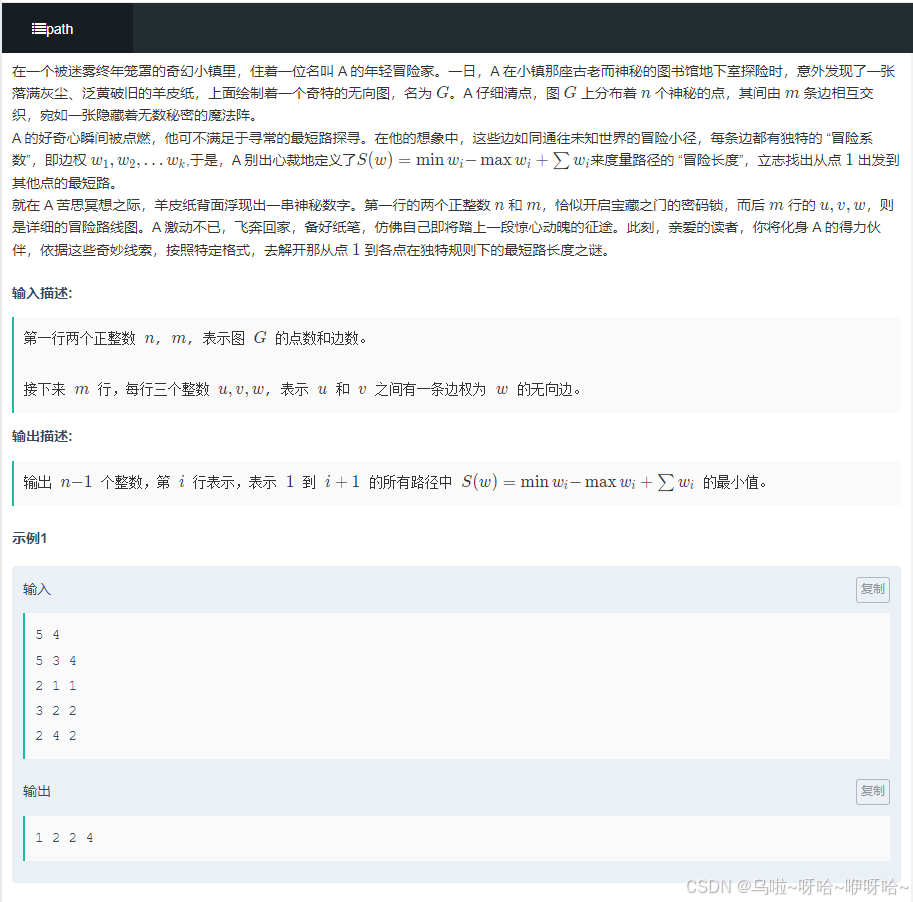
#include "bits/stdc++.h"
using namespace std;
using ll = long long;
using namespace std;
void solve()
{
    int n,m;
    cin>>n>>m;
    vector adj(n+1,vector<pair<int,ll>>());
    int u,v,w;
    for(int i = 0;i<m;i++){
        cin>>u>>v>>w;
        adj[u].push_back({v,w});
        adj[v].push_back({u,w});
    }
    vector dist(n+1,vector<ll>(4,1e18));
    dist[1][0] = 0;
    priority_queue<pair<ll,pair<int,int>>,vector<pair<ll,pair<int,int>>>,greater<pair<ll,pair<int,int>>>> pq;
    pq.push({0,{1,0}});
    while(!pq.empty()){
        auto it = pq.top();
        ll d = it.first;
        int u = it.second.first, wt = it.second.second;
        pq.pop();
        for(auto [v,w]:adj[u]){
            if(d+w<dist[v][wt]){
                dist[v][wt]= d+w;
                pq.push({d+w,{v,wt}});
            }
            if((wt&1)==0){ // 2 times
                if(d+w+w<dist[v][wt+1]){
                    dist[v][wt+1] = d+w+w;
                    pq.push({d+w+w,{v,wt+1}});
                }
            }
            if((wt&2)==0){ // 0 times
                if(d<dist[v][wt+2]){
                    dist[v][wt+2] = d;
                    pq.push({d,{v,wt+2}});
                }
            }
        }
    }
    for(int i = 2;i<=n;i++){
        cout<<min(dist[i][0],dist[i][3])<<" ";
    }
}

int main()
{
    ios_base::sync_with_stdio(false);cin.tie(0);cout.tie(0);
    int testcase = 1;
    while (testcase--)
        solve();
    return 0;
}

 

 

for (auto [v, w] : adj[u]) {
    // 1) 普通走法
    if (d + w < dist[v][wt]) {
        dist[v][wt] = d + w;
        pq.push({d + w, {v, wt}});
    }

    // 2) 如果可以用“多加一次” (bit0 == 0)
    if ((wt & 1) == 0) {
        // d + w + w
        if (d + 2LL*w < dist[v][wt + 1]) {
            dist[v][wt + 1] = d + 2LL*w;
            pq.push({d + 2LL*w, {v, wt + 1}});
        }
    }

    // 3) 如果可以用“少加一次” (bit1 == 0)
    if ((wt & 2) == 0) {
        // d + 0
        if (d < dist[v][wt + 2]) {
            dist[v][wt + 2] = d;
            pq.push({d, {v, wt + 2}});
        }
    }
}

 

 

 

 I.lucky number

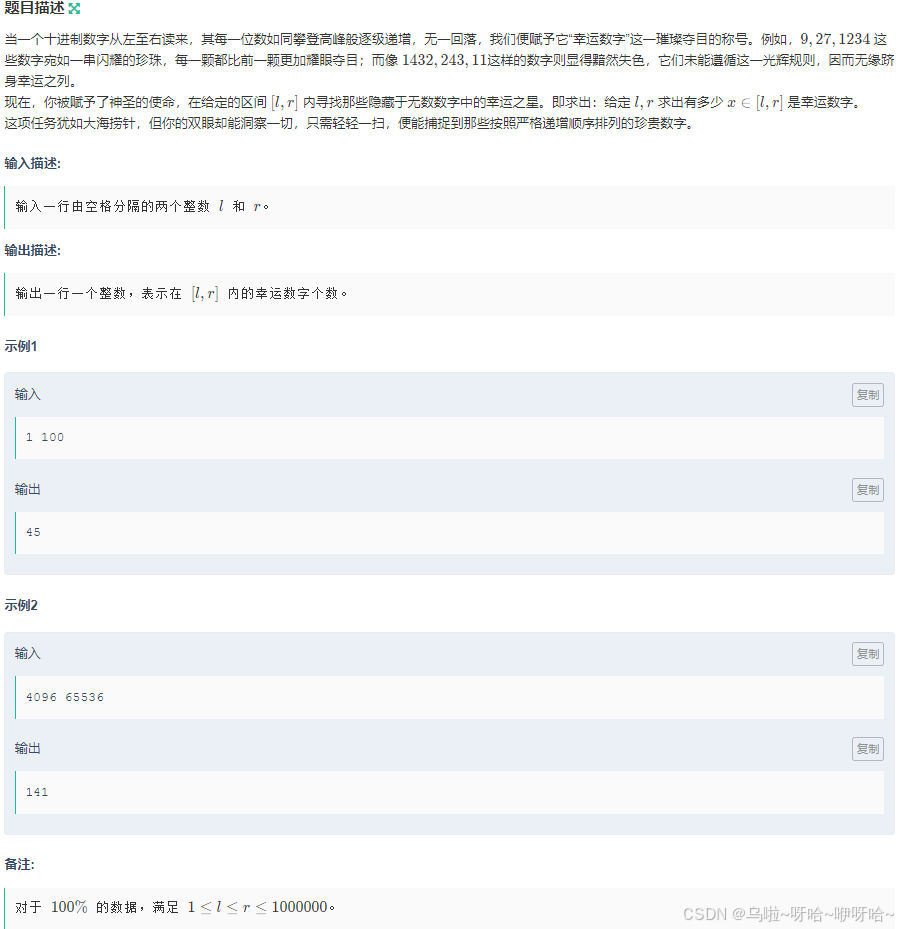
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
bool find(ll num){
	if(num>=1&&num<=9)return true;
	if(num%10==0)return false;
	vector<ll> a;
	while(num--){
		ll temp=num%10;
		a.push_back(temp);
		num/=10;
	}
	for(ll i=0;i<a.size()-1;i++){
		if(a[i]<=a[i+1])return false;
	}
	return true;
}
int main(){
	ll l,r;cin>>l>>r;
	ll sum=0;
	for(ll i=l;i<=r;i++){
		if(find(i)){
			//cout<<i<<endl;
			sum++;
		}
	}
	cout<<sum<<endl;
	return 0;
}

J.sequence

 

 

 


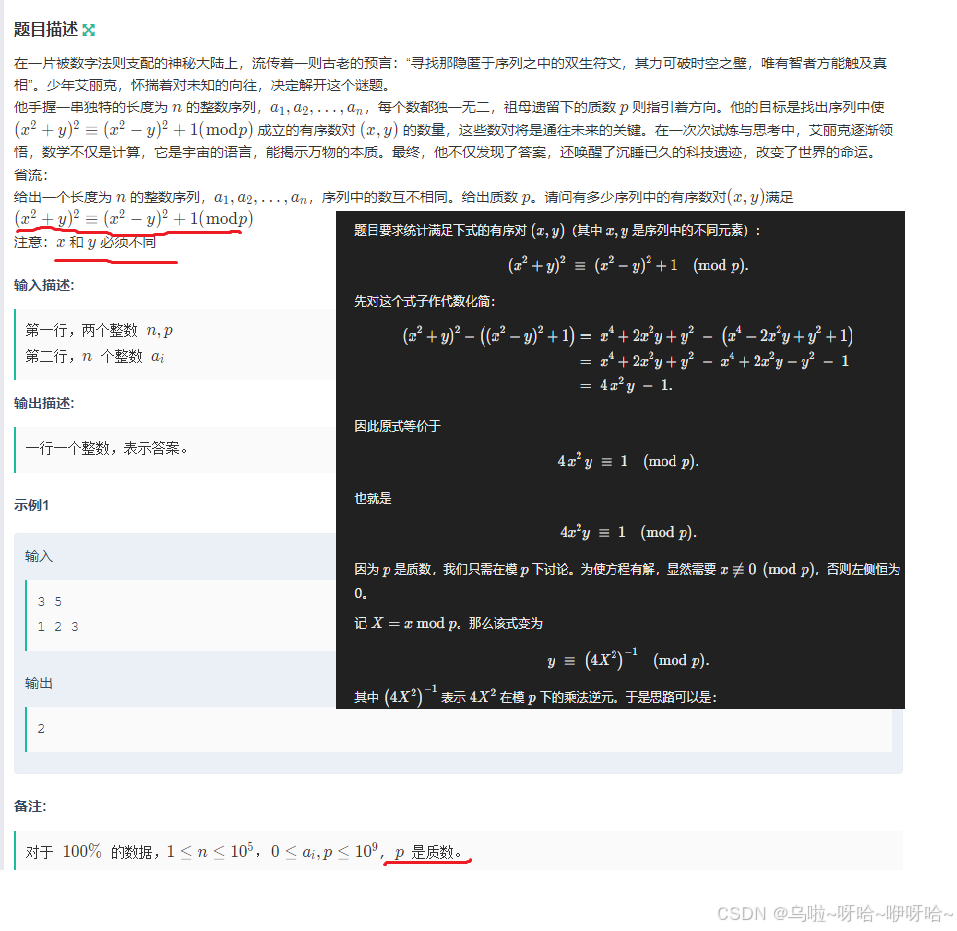
//y, (4x*x)^(-1)  mod  p是同一个余数
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,p;
map<ll,ll> modmod;
ll qsm(ll a,ll b){
	ll res=1;
	a%=p;
	while(b){
		if(b&1)res=a*res%p;
		a=a*a%p;
		b/=2;
	}
	return res;
}
int main(){
	cin>>n>>p;
	vector<ll> a(n);
	for(ll i=0;i<n;i++){
		cin>>a[i];
		modmod[4*a[i]%p*a[i]%p]++;
	}
	ll sum=0;
	for(ll i=0;i<n;i++){
		ll x=qsm(a[i],p-2);
		// 需要确定是否当前的 y 在序列中等于当前的 a[i]
		// 因为 y ≡ (4x^2)^(-1) mod p，且 a[i] ≠ y 仅当 a[i] ≠ y
		// 检查 a[i] 是否恰好等于 y
		// 由于 y 是模 p 的逆元，且序列中元素互不相同
		// 如果 y 在序列中存在且 y == a[i], 则需要减 1
		// 但 y 可能对应多个不同的元素在模 p 下同余于 y
		// 这里我们需要明确 y 是否等于当前 a[i]也即x
		// 因为 y = (4x^2)^(-1) mod p, 且y!=x
		// 所以 y == x 只有当 a[i] ≡ (4a[i]^2)^(-1) mod p 时
		if(x==0)continue;//无逆元，跳过
		if(x==(4*a[i]%p*a[i]%p))sum+=modmod[x]-1;
//括号里条件判断记得要注意优先级，还需要排除自身
		else sum+=modmod[x];
	}
	cout<<sum;
	return 0;
}

#include <bits/stdc++.h>
using namespace std;

using ll = long long;

// 快速幂计算 base^(exp) mod p （p 为质数）
// 用来求逆元时，exp = p-2
ll modExp(ll base, ll exp, ll p) {
    ll result = 1 % p;  // 应对 p=1 情况，不过题意p是质数且>=2
    base = (base % p + p) % p;
    while(exp > 0) {
        if(exp & 1) result = ( (__int128)result * base ) % p;
        base = ( (__int128)base * base ) % p;
        exp >>= 1;
    }
    return result;
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n;
    long long p;
    cin >> n >> p;  // n,p

    vector<long long> arr(n);
    for(int i = 0; i < n; i++){
        cin >> arr[i];
    }

    // 如果 p=1 或 p=2，特殊快速判断
    // - p=1不可能，因为p是质数
    // - p=2也很简单: 4*x^2*y mod 2=0 => 无法等于1 =>答案=0
    if(p == 2){
        cout << 0 << "\n";
        return 0;
    }

    // 统计每个模值出现次数
    // p 可达1e9, 无法直接开数组，只能用unordered_map或 map
    unordered_map<ll,int> freq;
    freq.reserve(n*2);   // 以防止频繁 rehash
    freq.max_load_factor(0.7f);

    auto modVal = [&](long long x){
        long long r = x % p;
        if(r < 0) r += p;
        return r;
    };

    for(auto &x : arr){
        ll r = modVal(x);
        freq[r]++;
    }

    long long ans = 0;
    // 遍历每个 x，计算可配对的 y 数量
    for(auto &x : arr){
        ll X = modVal(x);
        if(X == 0) {
            // 4*x^2 = 0 (mod p) => 不可能=1 => 跳过
            continue;
        }
        // T = 4 * X^2 mod p
        // 注意可能溢出，用 128 位中间量或先做 modMul
        // 这里做一步一步:
        long long X2 = ( (long long)X * X ) % p;    // x^2 mod p
        long long T  = (4LL * X2) % p;             // 4 x^2 mod p
        if(T == 0) {
            // 依然不可能得到1
            continue;
        }
        // T_inv = T^(p-2) mod p
        long long T_inv = modExp(T, p-2, p);

        // freq[T_inv] => 多少 y 的值 mod p = T_inv
        // 如果 X == T_inv, 需要排除 x 本身
        auto it = freq.find(T_inv);
        if(it == freq.end()){
            // 没有任何元素 y 满足 y mod p= T_inv
            continue;
        }
        long long cnt = it->second;
        if(X == T_inv) {
            // 要排除 x 本身(1个)
            cnt -= 1;
        }
        ans += cnt;
    }

    cout << ans << "\n";
    return 0;
}

path仔细看看，其他大部分转换一下不是很难，请继续前进。

 

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值