（二叉搜索树6-10）The Kth Largest in BST--C语言

Given a binary search tree, you are supposed to find the node that contains the K-th largest key.

Format of function:

BinTree KthLargest ( BinTree T, int K );

where BinTree is defined as the following:

typedef struct TNode *BinTree;
struct TNode{
int Key;
BinTree Left;
BinTree Right;
};

The function KthLargest is supposed to return the pointer that points to the node that contains the K-th largest key in the binary search tree T.

Here T is not empty and all its keys are distinct positive integers. K is positive and is never more than the total number of nodes in the tree.

Sample program of judge:

#include <stdio.h>
#include <stdlib.h>

typedef struct TNode *BinTree;
struct TNode{
    int Key;
    BinTree Left;
    BinTree Right;
};

BinTree BuildTree(); /* details omitted */
BinTree KthLargest ( BinTree T, int K );

int main()
{
    BinTree T, P;
    int K;

    T = BuildTree();
    scanf("%d", &K);
    P = KthLargest(T, K);
    printf("%d\n", P->Key);
    if (P->Left) printf("%d\n", P->Left->Key);
    else printf("NULL\n");
    if (P->Right) printf("%d\n", P->Right->Key);
    else printf("NULL\n");

    return 0;
}
/* Your function will be put here */

Sample Input: (for the following tree)

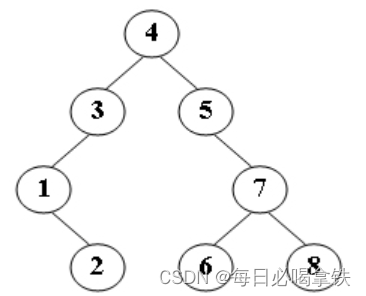
4

Sample Output:

5
NULL
7

Analysis:

用中序遍历得到序列，因为是二叉搜索树，则该序列一定是递增的，所以直接返回序列中倒数第k个数（下标为count-k），count为序列总数。

Notice：

• 如果不知道怎么用中序遍历得到序列，可以去看是否二叉搜索树，在这篇文章中，我具体分析了中序遍历得到序列。
• 序列中储存的是地址，因此直接返回即可。

Code:

BinTree KthLargest ( BinTree T, int K )
{
    BinTree BT=T; 
    BinTree a[100]={NULL},b[100]={NULL};
    int ai=0,bi=0;
    while(BT||ai!=0)
    {
        while(BT)
        {
            a[ai++]=BT;
            BT=BT->Left;
        }
        if(a[ai-1]==NULL)
            ai--;
        int top=--ai;
        b[bi++]=a[top];
        BT=a[top];
        a[top]=NULL;
        BT=BT->Right;
    }
    return b[bi-K];
}