最全总结【时间序列】时间序列的预处理和特征工程

本次分享的内容主要是时间序列，什么是时间序列，时间序列的预处理应该怎么做，时间序列的特征工程都有什么操作。包含了季节性分解，平稳性检验，滑动窗口等

时间序列数据预处理与分析

什么是时间序列？

时间序列（Time Series）是按时间顺序排列的一组数据点，通常用于描述和分析随时间变化的现象。时间序列数据在许多领域中都有广泛应用，如金融市场、气象学、经济学、医学等。

时间序列的组成

时间序列通常包含以下几部分组成：

1. 趋势（Trend）：时间序列的长期变化方向，表示数据随时间的整体上升或下降趋势。
2. 季节性（Seasonality）：时间序列中随季节变化的周期性波动，通常是年、月或季度等周期性的波动。
3. 周期性（Cyclicality）：时间序列中较长周期的波动，通常与经济周期、社会周期等相关，但与季节性不同，周期的时间长度不固定。
4. 随机波动（Noise）：时间序列中的随机成分，表示无法预测的变化。

解释

1. 趋势（Trend）
   趋势指的是时间序列数据在长时间跨度内的整体上升或下降方向。例如，股票市场的长期上涨趋势、气温的季节性变化等，都是趋势的一种表现。
   趋势通常表现为一种持续的、方向性变化，且与季节、周期等因素无关。因此，在建模时，去除趋势成分可以使得模型更加专注于数据的短期波动和周期性特征。

2. 季节性（Seasonality）
   季节性是指数据在固定周期内的规律性波动。例如，零售销售数据在每年的假日季节通常会大幅上升，或者气温在每年春夏秋冬季节之间会有规律的波动。季节性波动往往与年度、季度、月度或周度等时间周期密切相关。
   季节性可以通过周期性的模式来预测，因此对季节性进行建模有助于提高模型的准确性。

3. 周期性（Cyclicality）
   与季节性类似，周期性是指时间序列中较长周期的波动，但其周期长度不固定。周期性波动通常与宏观经济周期、社会活动周期等因素相关。周期性波动的时间跨度不固定，可能持续数年。
   周期性的变化往往比较复杂，且难以精确预测，因为其波动周期不如季节性那样固定。

4. 随机波动（Noise）
   随机波动是指时间序列中无法通过其他成分（如趋势、季节性或周期性）解释的随机成分。它代表了无法预测的部分，可能由测量误差、外部不可控因素或自然波动所导致。
   去除噪声和无关的随机波动是时间序列分析中非常重要的步骤，因为噪声往往会干扰模型的学习和预测。

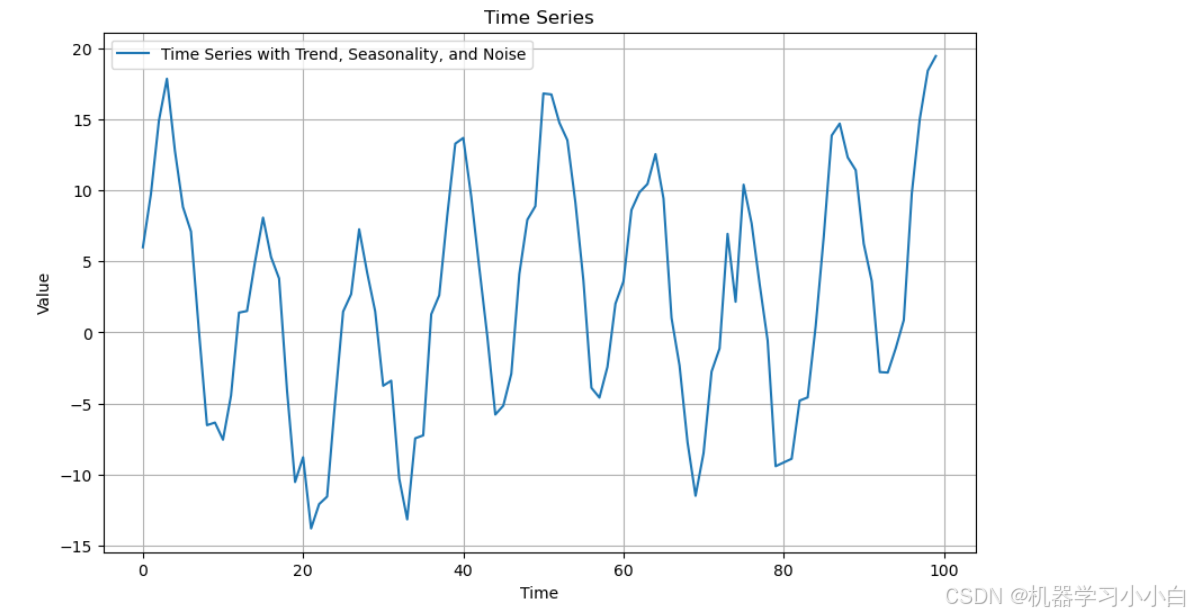
以下就是一个时间序列，包含了趋势，周期性，季节性和随机波动

import numpy as np
import matplotlib.pyplot as plt

# 设置随机种子，确保每次生成相同的结果
np.random.seed(42)

# 生成时间序列的时间范围
time = np.arange(0, 100, 1)

# 定义趋势部分 (线性趋势)
trend = 0.05 * time

# 定义季节性部分 (周期性波动)
seasonal = 10 * np.sin(2 * np.pi * time / 12)

# 定义周期性部分 (更长周期的波动)
cycle = 5 * np.cos(2 * np.pi * time / 50)

# 定义随机波动 (噪声)
noise = np.random.normal(0, 2, size=len(time))

# 将所有部分合成一个时间序列
data = trend + seasonal + cycle + noise

# 绘制图像
plt.figure(figsize=(10, 6))
plt.plot(time, data, label='Time Series with Trend, Seasonality, and Noise')
plt.title('Time Series')
plt.xlabel('Time')
plt.ylabel('Value')
plt.legend(loc='upper left')
plt.grid(True)
plt.show()

时间序列的数学模型

假设时间序列 $(y_t)$ 可以由以下几个部分组成：
$$y_t=T_t+S_t+C_t+{ϵ}_t$$

• $(T_t)$是趋势成分，表示时间序列中的长期变化；
• $(S_t)$ 是季节性成分，表示随季节变化的波动；
• $(C_t)$ 是周期性成分，表示与时间周期相关的波动；
• $({ϵ}_t)$ 是随机波动（噪声），表示无法预测的变化。

在某些情况下，如果没有周期性成分，模型可以简化为：

$$y_t=T_t+S_t+{ϵ}_t$$

一 时间序列数据预处理的必要步骤

时间序列数据的预处理是建立有效模型的基础。预处理的目标是通过清洗、转换和特征生成等步骤，增强数据的可用性，去除噪音，帮助模型捕捉更有价值的模式。常见的时间序列数据预处理步骤包括：数据清洗、缺失值处理、平稳化、特征生成等。

1. 数据清洗

1.1 去除重复值

去除时间序列中的重复值是第一步，确保每个时间戳对应唯一的观测值。

df = df.drop_duplicates(subset=['timestamp'], keep='last')

1.2 处理异常值

时间序列中的异常值可能导致模型误差。使用Z-Score或箱型图等方法可以帮助我们检测和处理异常值。

from scipy import stats
z_scores = stats.zscore(df['value'])
df = df[(z_scores < 3) & (z_scores > -3)]

1.3 处理缺失值

时间序列数据中缺失值的处理方法有多种，可以选择删除、插值或填充等策略。

2. 时间戳处理

2.1 确保时间格式一致

统一时间戳的格式非常重要，确保时间列可以被正确解析。

df['timestamp'] = pd.to_datetime(df['timestamp'])

2.2 设置时间索引

为了方便时间序列分析和可视化，可以将时间戳设置为 DataFrame 的索引。

df.set_index('timestamp', inplace=True)

二、时间序列预处理的关键步骤

大多数时间序列模型（如ARIMA）要求数据是平稳的，意味着数据的均值和方差是常数，且没有季节性或趋势。接下来将基于常用的 LSTM（长短期记忆网络） 进行数据平稳化的讨论，并解释如何在深度学习模型中处理时间序列的平稳性问题。

数据平稳化与LSTM

在时间序列建模中，LSTM（Long Short-Term Memory）是一种常用于处理时间序列数据的递归神经网络（RNN）。LSTM特别适用于捕捉时间序列数据中的长期依赖关系。然而，尽管LSTM有很强的建模能力，但它并不能自动处理时间序列数据的平稳性问题。平稳性是时间序列分析的一个关键概念，对于某些模型（如ARIMA），要求数据是平稳的，但对于LSTM等深度学习模型，虽然它能捕捉趋势、季节性和周期性，但仍然需要进行一定的平稳化处理以提高模型的效果。

单位根检验

我们可以通过Augmented Dickey-Fuller（ADF）检验来测试时间序列是否平稳。平稳的时间序列应当通过检验。

from statsmodels.tsa.stattools import adfuller
result = adfuller(df['value'])
print(f'p-value: {result[1]}')

一般情况下认为如果 p-value 小于0.05，则认为数据是平稳的。

1. 为什么需要平稳化？

平稳性指的是时间序列的统计特性（如均值、方差）随时间变化保持不变。对于非平稳时间序列，直接应用LSTM进行训练可能会导致模型过拟合或预测不准确。因此，通常需要对数据进行平稳化处理。

2. LSTM的平稳化方法

对于LSTM而言，数据的平稳化步骤通常包括以下几种常见方式：

• 差分（Differencing）
• 对数变换（Log Transformation）
• 去趋势（Detrending）
• 标准化（Normalization）或归一化（Scaling）

3. 使用LSTM的时间序列预处理

以下是通过 LSTM 进行时间序列预测时，如何处理平稳化的步骤及其示例代码。

3.1 差分

差分是一种常用的平稳化方法，它通过计算当前值与前一时刻值之间的差异来去除时间序列中的趋势。一次差分的公式为：

$$y_t^{\prime }=y_t-y_{t-1}$$
在LSTM应用中，差分处理后通常有助于消除数据中的长期趋势，使得序列更加平稳。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

df['value'] = df['value'].diff().dropna()  # 进行一次差分

# 绘制差分后的数据
plt.figure(figsize=(10,6))
plt.plot(df['value'])
plt.title('Differenced Time Series')
plt.show()

3.2 对数变换

对于具有指数增长趋势的时间序列，使用对数变换可以使得数据变得更加平稳。例如，使用对数变换后，数据的变化通常变得更加线性。

$$y_t^{\prime }=\log (y_t)$$

df['value'] = np.log(df['value'])  # 对数变换

3.3 去趋势（Detrending）

去趋势是指从时间序列中去除长期的趋势成分。去趋势的目的是为了消除时间序列中的长期变化，使数据更加平稳。常见的去趋势方法包括：

• 差分法：计算时间序列中相邻数据点之间的差值，用来消除趋势成分。
• 滚动平均法：通过计算滚动窗口内的数据均值，作为趋势成分并将其从数据中减去。
  例如，使用滚动窗口来计算趋势并去除它：

# 使用滚动窗口计算趋势
df['trend'] = df['value'].rolling(window=12).mean()
df['detrended'] = df['value'] - df['trend']

3.4 去季节性（Deseasonalizing）

去季节性是指消除时间序列中的季节性成分。季节性成分通常表现为固定周期的波动，可以使用 季节性分解 技术（如 STL 分解、X-12-ARIMA）将时间序列分解为趋势、季节性和残差成分。去季节性的过程通常包括以下步骤：

提取季节性模式。
从原始数据中减去季节性成分，得到去季节性后的数据。

3.5 标准化与归一化

标准化和归一化是数据预处理中的重要步骤，目的是将数据缩放到一个统一的范围内。标准化的目的是使得数据的均值为0，方差为1；而归一化通常是将数据缩放到0到1的范围内。
标准化公式为：

$$y_t^{\prime }=\frac{y_t-\mu }{\sigma }$$

其中，$\mu$ 是数据的均值，$\sigma$ 是标准差。

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
df['value_scaled'] = scaler.fit_transform(df[['value']])

# 绘制标准化后的数据
plt.figure(figsize=(10,6))
plt.plot(df['value_scaled'])
plt.title('Standardized Time Series')
plt.show()

三、时间序列的特征工程

特征工程是提升模型性能的关键步骤。对于时间序列数据，特征工程主要包括以下几方面：

1. 滞后特征（Lag Features）

滞后特征是指基于过去的时间点创建的特征。这些特征能够捕捉时间序列中的自相关性，有助于模型了解当前值与过去值之间的关系。常见的滞后特征包括：

• 滞后1期（Lag-1）：前一时刻的值。
• 滞后2期（Lag-2）：前两时刻的值。
• 滞后N期（Lag-N）：前N时刻的值。
  例如，创建一个滞后特征的代码示例如下：

# 创建滞后特征
df['lag1'] = df['value'].shift(1)
df['lag2'] = df['value'].shift(2)

2. 滚动统计量（Rolling Statistics）

滚动统计量是通过滑动窗口计算时间序列的统计特征，例如滚动均值、滚动标准差等。这些特征能够捕捉局部的趋势和波动，对于揭示时间序列的动态特征非常有用。

# 计算滚动均值和滚动标准差
df['rolling_mean'] = df['value'].rolling(window=12).mean()
df['rolling_std'] = df['value'].rolling(window=12).std()

3. 季节性特征

如果时间序列存在季节性波动，可以基于日期或时间戳创建季节性特征。例如，提取年份、月份、季度等特征，帮助模型学习季节性波动。

# 提取季节性特征
df['month'] = df['date'].dt.month
df['quarter'] = df['date'].dt.quarter

4. 时间窗口特征

时间窗口特征是指在特定时间窗口内（例如过去7天或过去30天）计算统计量。通过这些统计量，模型可以捕捉数据的短期波动。

# 计算过去7天的移动平均
df['7_day_avg'] = df['value'].rolling(window=7).mean()

四、总结

时间序列的预处理和特征工程是提高时间序列预测模型效果的关键步骤。通过对数据进行去趋势、去季节性、平稳化等预处理操作，可以有效减少噪声并突出数据的规律性。同时，通过滞后特征、滚动统计量、季节性特征等特征工程方法，可以更好地捕捉时间序列的动态变化。掌握这些技巧将帮助你在时间序列分析中取得更好的效果，为预测模型提供有力的支持。

五 答疑

看到最后，相信很多小伙伴心里会有疑问，为什么在时间序列预处理时要去除趋势、季节性等操作，而在特征工程中又要通过时间窗口特征、滚动统计量、滞后特征等方法捕获这些趋势、季节性和周期性？

这个问题看似有些矛盾，但实际上两者的操作是基于不同的目标和需求。在时间序列预处理阶段，我们希望将数据转换为更加适合建模的形式；而在特征工程阶段，我们则通过引入一些特征来提升模型的预测能力。下面将分别详细分析这两者之间的差异及其原因。

一、时间序列预处理：去除趋势、季节性等操作

在时间序列的预处理阶段，主要目标是将数据转化为更加平稳且适合建模的形式。以下是去除趋势和季节性的一些关键原因：

1. 去除趋势

趋势是数据中的长期变化（例如股市的长期上涨或下跌）。去除趋势的原因有：

减少长期波动的干扰：对于很多时间序列模型（如ARIMA），如果数据中有强烈的趋势成分，模型可能会忽略短期的波动，导致预测结果不准确。
满足平稳性假设：许多经典的时间序列模型（例如ARIMA）要求数据必须是平稳的。去除趋势有助于使数据的均值和方差不随时间变化，从而满足平稳性要求。

2. 去除季节性

季节性是指数据中在某一固定周期内的规律性波动（如每年的天气变化或节假日效应）。去除季节性的操作主要是为了：

减少周期性波动的干扰：季节性波动可能掩盖其他类型的波动，去季节性处理可以让模型专注于非季节性的模式。
保持平稳性：如果数据的季节性较强，均值和方差会在不同的季节内变化，从而不满足平稳性要求。去除季节性有助于使数据更加平稳。

3. 去除噪声

噪声是指数据中随机、不规则的波动，去除噪声有助于清理数据，让模型能够专注于更有意义的信号。

二、特征工程：捕获趋势、季节性等特征

在特征工程阶段，我们的目标是通过提取有意义的特征来增强模型的预测能力。在这个阶段，趋势、季节性和周期性成分是有价值的信息，因此我们通过一些方法再次捕获这些成分。以下是特征工程中常用的一些方法：

1. 滞后特征（Lag Features）

滞后特征是通过参考过去的观测值来生成的新特征。例如，过去一段时间的观测值对当前时刻的预测可能具有重要作用。

即使数据中存在趋势或季节性，过去的数据仍包含了有价值的信息。通过滞后特征，我们可以捕捉到数据的自相关性（即，过去的值对未来的影响）。

2. 时间窗口特征

时间窗口特征通过计算过去一段时间内的统计量（如均值、标准差等），帮助模型捕捉局部波动和短期趋势。例如，过去7天的平均销售额可能对今天的销售额预测有帮助。

这些特征帮助模型理解数据的短期动态变化，尤其是在存在季节性和周期性波动时，时间窗口特征能够揭示这些规律。

3. 滚动统计量（Rolling Statistics）

滚动统计量是对时间序列数据进行滑动窗口操作，计算出每个时间点的窗口内统计值（如滚动平均、滚动标准差等）。这种方法能够：

捕捉数据中的局部趋势和波动，尤其在存在季节性变化时，能够帮助模型理解短期内的波动性。

4. 季节性特征

季节性特征是通过编码时间周期信息（如月份、季度、星期几等）来增强模型对周期性波动的理解。

在许多应用场景中（例如零售、气象等），季节性变化对数据有重要影响，模型通过加入季节性特征能够捕捉到这些周期性的波动，从而提高预测的准确性。
三、总结
预处理阶段：目标是简化数据，去除不必要的复杂性，通常通过去除趋势、季节性等成分来使数据更加平稳，并减少无关成分的干扰。这有助于一些模型（如ARIMA）更好地拟合数据。

特征工程阶段：目标是构建新的特征，增强模型的预测能力。在这个阶段，趋势、季节性和周期性是有价值的信息，我们通过滞后特征、时间窗口特征、滚动统计量和季节性特征等方法来捕捉这些模式。

通过这两者的结合，我们能够有效地处理时间序列数据，从而在模型训练时提升预测的准确性和鲁棒性。

拓展----滤波器

时间序列中的滤波器（Filter）是一种数学工具，通常用于平滑或去除数据中的噪声，或者提取信号的特定特征，如趋势、季节性或周期性。滤波器的目标是通过消除不需要的波动（如随机噪声）或强调特定模式（如趋势或周期性）来改善时间序列数据的质量，从而使分析更加准确。

在时间序列分析中，滤波器主要有以下几种常见类型：

1. 低通滤波器（Low-pass filter）

作用：去除数据中的高频噪声，保留较低频率的信号。
应用：用于平滑时间序列数据，去除随机波动，保留长期趋势或季节性模式。
例子：常见的平滑滤波器（如移动平均），它通过取一定范围内的平均值来去除短期波动。

2. 高通滤波器（High-pass filter）

作用：去除时间序列中的低频部分，保留高频成分。
应用：用于提取数据中的变化趋势或突变，去除长期趋势部分。
例子：常用在分析周期性数据时，去掉长期趋势，只关注周期性变化。

3. 带通滤波器（Band-pass filter）

作用：保留特定频段内的信号，去除低于和高于该频段的成分。
应用：用于分析特定频率范围内的周期性波动，通常用于周期性的时间序列数据分析。

4. 加权移动平均滤波器（Weighted Moving Average Filter）

作用：通过给时间序列中的不同数据点分配不同的权重，对数据进行平滑。
应用：常用于消除短期波动，平滑数据并突出长期趋势。

5. 指数加权移动平均（Exponential Moving Average, EMA）

作用：与传统的移动平均不同，EMA给近期数据赋予更高的权重，适应性更强。
应用：特别适用于金融时间序列数据，可以有效捕捉短期波动。

6. 中值滤波器（Median Filter）

作用：通过取滑动窗口内的中位数来代替窗口内的每个数据点，从而去除异常值或尖锐的噪声。
应用：常用于去除时间序列中的极端异常值，尤其是在信号中有突发噪声时。

滤波器的主要用途：

1. 平滑时间序列：去除噪声，保留信号的整体趋势或季节性变化。
2. 去除趋势或季节性：通过使用高通或带通滤波器，可以去除时间序列中的长期趋势或季节性，帮助专注于周期性成分。
3. 数据降噪：通过去除随机波动或高频噪声，提供更清晰的信号。
4. 特征提取：帮助从复杂的时间序列中提取感兴趣的特征（如趋势、周期等）。

滤波器的选择：

滤波器的类型和参数选择通常取决于数据的性质以及分析的目标。例如，如果你希望保留一个时间序列中的长期趋势，可能会选择低通滤波器；如果你希望提取周期性的变化，带通滤波器或高通滤波器可能更适合。
总结来说，滤波器在时间序列分析中扮演着至关重要的角色，可以帮助我们提取和理解数据中的重要模式，同时去除干扰因素。

代码示例

import statsmodels.api as sm

# 使用标准的 λ = 1600 进行 HP 滤波
cycle, trend = sm.tsa.filters.hpfilter(train_df1['y'], lamb=1600)

# 导入绘图所需的库
import matplotlib.pyplot as plt
from matplotlib import rcParams

# 创建一个指定大小的图形
plt.figure(figsize=(20, 6))

# 绘制原始数据
plt.plot(train_df1['y'], label='Original Data')

# 绘制去趋势后的趋势部分
plt.plot(trend, label='Detrended Trend Component', color='red')

# 添加图例，标注每个数据线
plt.legend()

# 添加图表标题
plt.title('HP Filter Detrending')

# 显示图表
plt.show()