💫二叉树的结点结构定义
typedef struct BinaryTreeNode
{
int val;
struct BinaryNode* left;
struct BinaryNode* right;
}BTNode;
💫创建一个二叉树结点
我们来写一个函数BuyNode(x)函数用于创建二叉树结点。
用动态开辟函数malloc函数进行动态开辟,并强制转换为BTNode型,用变量node来去管理开辟的空间。
我们初始化结点,其val即为传入的参数x,左右指针left和right都设为NULL。
//创建一个二叉树结点
BTNode* BuyNode(int x)
{
BTNode* node = (BTNode*)malloc(sizeof(BTNode));
if (node == NULL)
{
perror("malloc fail");
}
else
{
node->val = x;
node->left = NULL;
node->right = NULL;
}
}
💫在主函数中手动创建一颗二叉树

我们在主函数中创建上面这样一颗二叉树。
首先,我们需要开辟6个结点,但此时6个结点之间没有任何的联系,我们需要改变其中一些结点的指针域left和right,来使得结点之间产生联系。
int main()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
node1->left = node2;
node1->right = node4;
node1->right=node3;
node2->left = node4;
node3->left = node5;
node3->right = node6;
return 0;
}
💫二叉树的前序遍历
首先,我们先要了解以下二叉树前序的前序遍历。
二叉树的前序遍历:
根-->左子树-->右子树
对于我们上面的这颗二叉树:
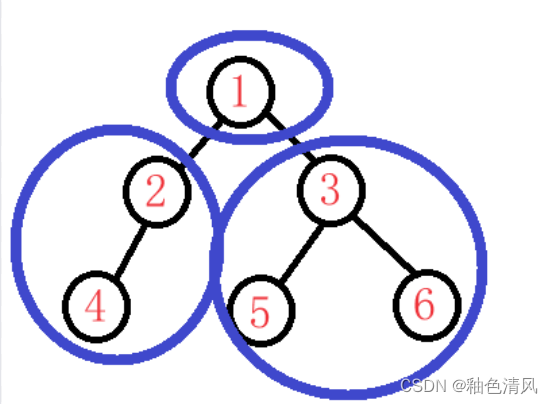
1-->左-->右
左子树和右子树也采用前序遍历的方式:

左子树:
2-->4
右子树
3-->5-->6
所以这颗二叉树的前序遍历为:
1-->2-->4-->3-->5-->6
正是由于这样的思想,将一个树根-->左-->右的左和右仍然是一颗树,接着再拆分…直到左子树和右子树的左右结点为空时。
所以这样的思想,我们就利用递归的想法就可以完成一颗二叉树的遍历。
💫调用栈递归——实现前序遍历
调用栈:程序在执行时,如果程序调用一个函数,它会先把这个函数压入栈中,等到这个函数返回结果(return )后,它才会从栈中弹出。
递归程序在执行时,会不断地调用自身,把函数压入栈中,当最后一个函数,也就是基线条件出现时,再逐渐清空栈空间。
下面我们根据这段代码来画图理解一些递归的思想。
//递归前序遍历一棵树
void PreOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL");
return;
}
printf("%d", root->val);
PreOrder(root->left);
PreOrder(root->right);
return 0;
}

我们按照步骤来执行以下程序:
①主函数中进行了函数调用,参数为node1
压栈:

node1不为空,打印结点:

②执行PreOrder(root->left),再次调用函数,参数为node2
进行压栈:

node2不为空,打印

③执行PreOrder(root->left),再次调用函数,参数为node4,压栈:

node4不为空,打印:

④执行PreOrder(root->left),再次调用函数,参数为NULL,压栈:

这是函数参数为NULL,进入if语句,进行打印 ,并return返回,这时出栈。



⑤y由于这段代码,当函数的参数为node4时,PreOrder(node4->left)已经有return,所以这时,程序会接着往下面执行PreOrder(node4->right)
这时再次调用函数,函数参数为NULL,压栈,打印,再出栈。



⑥ 这时对于函数PreOrder (node4)已经执行完语句 PreOrder(node4->left)和语句PreOrder(node4->right)了,后执行 return 0,函数有返回结果,所以出栈。
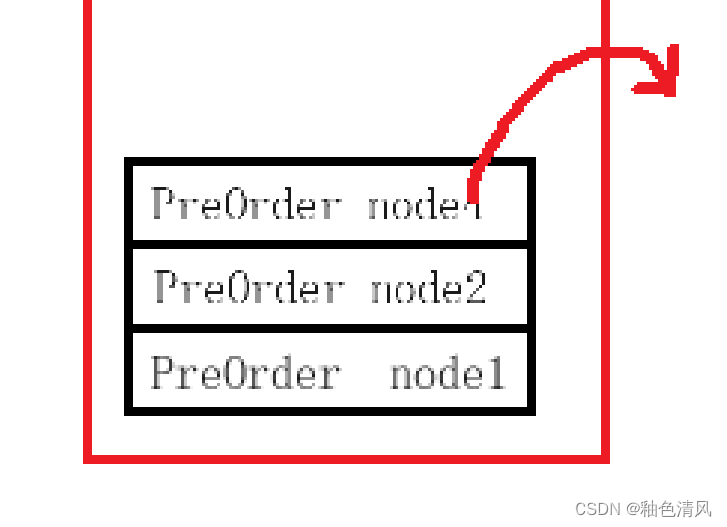

⑦此时,我们该执行 node2的右结点了。
对于PreOrder(node2->right)中,函数函数即是NULL,所以先压栈,然后打印,然后出栈。




⑧此时,函数PreOrder(node2) 的PreOrder(node2->left) 和PreOrder(node2->right) 都已经执行完了,即已经对node2结点的左右子树遍历完成,执行return 0 返回,这时PreOrder(node2) 出栈。


在此时,我们已经对node1的左子树遍历完成,接下来同遍历左子树一样,我们对右子树进行遍历。




这时输出为:

💫递归实现中序和后序遍历
根据上面前序的递归,我觉得最重要的代码是:
if (root == NULL)
{
printf("NULL");
return;
}
它是递归中能否回溯的一个关键。
下面写中序遍历:
//递归中序遍历二叉树
void Order(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
Order(root->left);
printf("%d ", root->val);
Order(root->right);
return 0;
}
递归后序遍历一棵树:
//递归后序遍历一颗二叉树
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->val);
return 0;
}
前中后序遍历结果分别为:
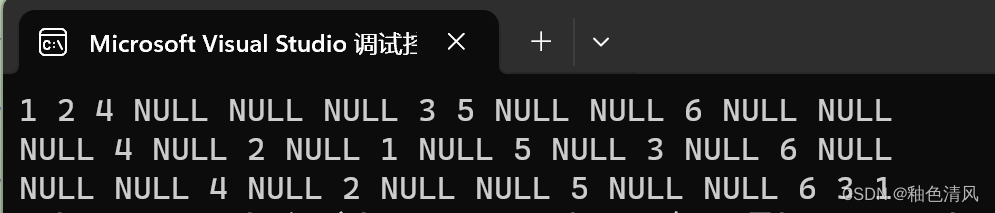








 本文详细介绍了二叉树的节点结构,动态创建二叉树节点,以及前序、中序和后序遍历的递归实现过程。通过实例展示了如何在主函数中手动构建二叉树,并通过调用栈理解递归遍历的逻辑。
本文详细介绍了二叉树的节点结构,动态创建二叉树节点,以及前序、中序和后序遍历的递归实现过程。通过实例展示了如何在主函数中手动构建二叉树,并通过调用栈理解递归遍历的逻辑。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










