*线性回归



w称为权重,决定了每个特征对我们预测值的影响 b称为偏置

*神经网络


 *损失函数
*损失函数

*训练数据集越大越好

*训练损失(最小化损失决定参数)

*梯度法(最小值)
神经网络在学习时找到最优的参数(权重和偏置)——指损失函数取最小值时的参数。
梯度指示的反向是各点处的函数值减小最多的方向
*基础优化算法(最低处,箭头越大)
像这样的由全部变量的偏导数汇总而成的向量称为梯度(gradient)。
我们发现梯度指向函数的“最低处”(最小值),就像指南针一样,所有的箭头都指向同一点。其次,我们发现离“最低处”越远,箭头越大。

*!!!
梯度指示的反向是各点处的函数值减小最多的方向,所以无法保证梯度所指的方向就是函数的最小值或者真正应该前进的方向。 但沿着它的方向能最大限度的减小函数的值。所以在寻找函数的最小值的位置任务中,以梯度的信息为线索,决定前进的方向。
流程:在梯度法中,函数的取值从当前位置沿着梯度方向前进一定的距离,然后在新的方向重新求梯度,再沿着新梯度的方向前进,如此反复,不断的沿梯度方向前进。
*随机梯度下降
不断的在损失函数递减的方向上更新参数来降低误差。


*小批量随机梯度下降

*选择批量值

*总结
梯度下降通过不断的沿着反梯度方向更新参数求解 小批量随机梯度下降是深度学习默认的求解算法 两个重要的超参数是批量大小和学习率
*softmax回归

*回归和分类
回归估计一个连续值
分类预测一个离散类别
MNIST:手写数字进行分类 (10 类)

ImageNet:对自然对象进行分类 (1000 类)

*kaggle上的分类任务

将维基百科上的恶语评论分为7类

*回归到分类多类
回归 单个连续数值输出 自然区间 与真实值的区别作为损失

分类 通常多个输出 输出的i表示预测为第i类的置信度

独热编码

使用均方损失训练 最大值作为预测

一个单层神经网络; 由于计算每个输出o1,o2,o3取决于所有输入x1、x2、x3和x4,因此softmax回归层也是全连接层。

输出层的神经元数量需要根据待解决的问题来决定。对于分类问题,输 出层的神经元数量一般设定为类别的数量。
比如:对于某个输入图像,预测是图中的数字0到9中的哪一个的问题( 10类别分类问题),将输出层的神经元设定为10个。
softmax运算(非负为1)

Softmax回归是一个多类分类模型 使用Softmax操作得到每个类的预测置信度

*损失函数

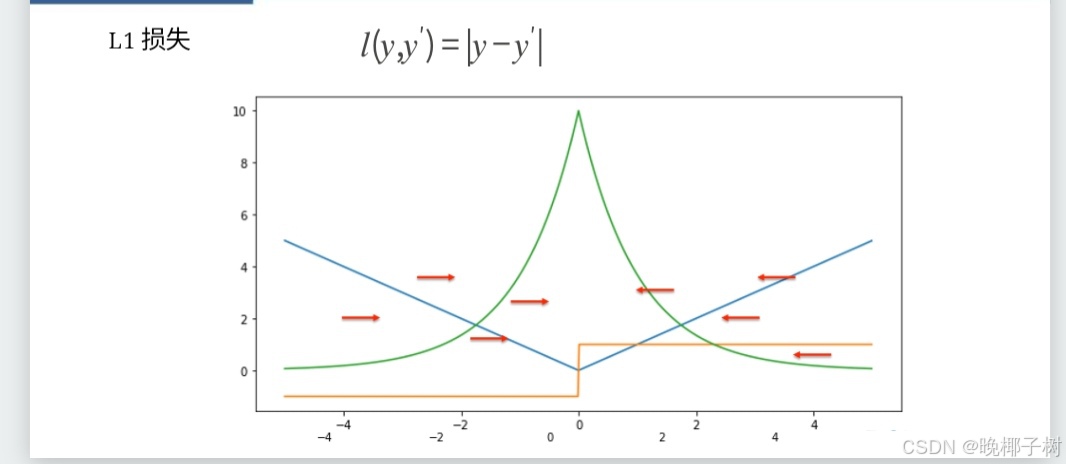
*Huber损失

*交叉熵损失
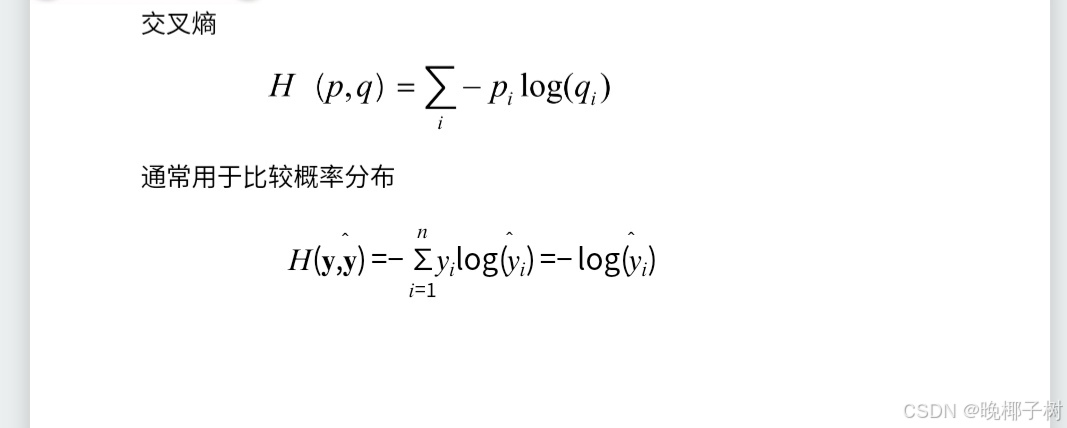





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








