2. 信息的表示和处理
无符号(unsigned)编码,补码(two’s-complement)编码,浮点数(floating-point)编码
当结果太大,无法用规定的有限数量的位表示,某些运算会溢出(overflow)
浮点运算是不可结合的
本章讨论计算机中的数学表示和运算
2.1 信息存储
机器级程序将内存和思维一个非常大的字节数组,称为虚拟内存(virtual memory)
2.1.1 十六进制表示法
C语言中,0xFa1D37b是合法的十六进制数
2.1.2 字数据大小
字长(word size)指明指针数据的标称大小(normal size),决定虚拟地址空间的最大大小
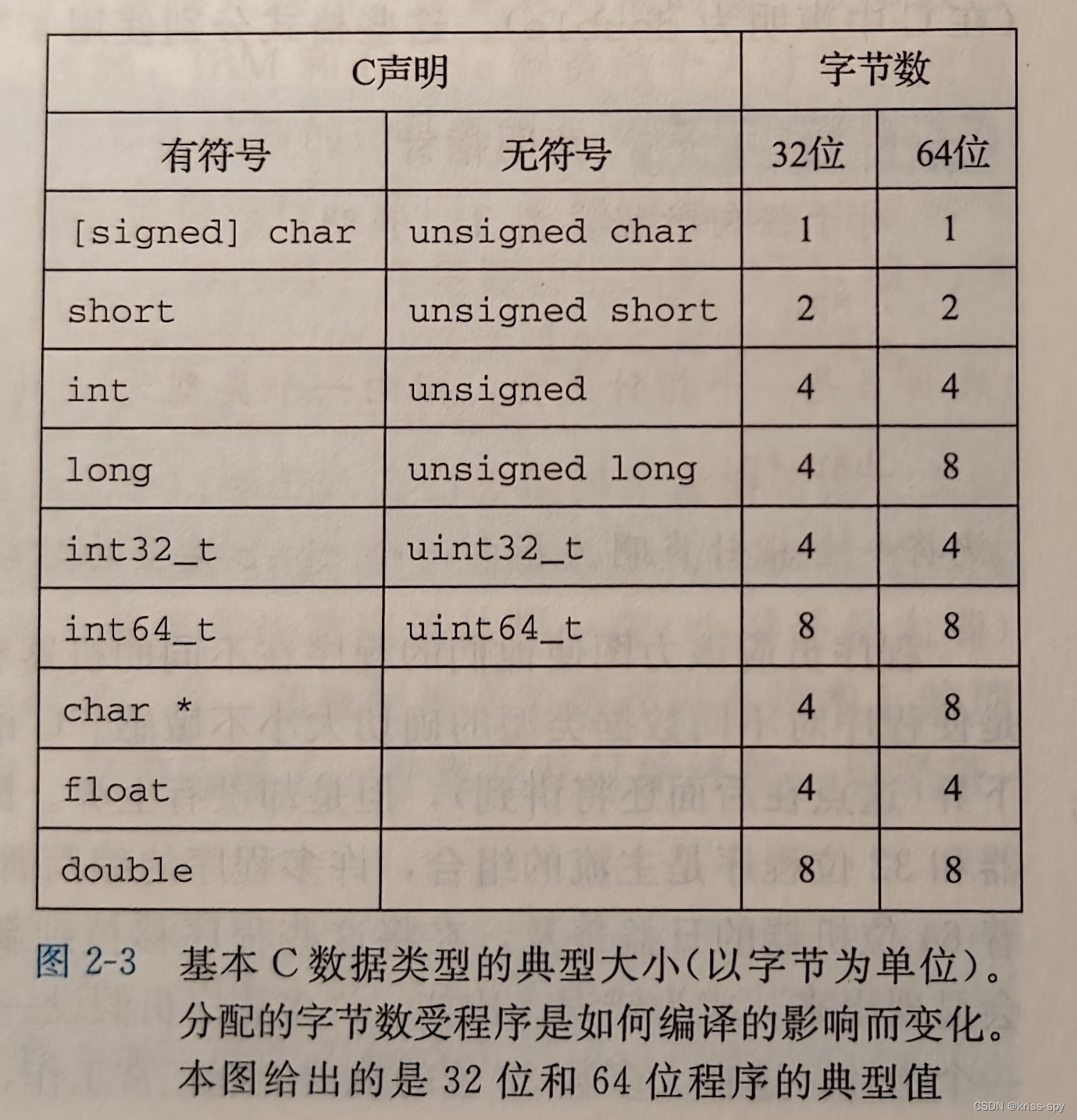
可移植性的一个方面就是使程序程序对不同数据类型的确切大小不敏感
2.1.3 寻址和字节顺序
一般地,多字节对象都被存储为连续的字节序列,对象的地址为所使用的字节中最小的地址
小端法(little endian),最低有效字节在最前面
大端法(big endian),最高有效字节在最前面
大多数Intel兼容机都只用小端模式
实际上两者没有技术上的优劣之分,但要注意兼容方法
例如,网络应用程序的代码编写必须遵守已建立的关于字节顺序的规则
2.1.4 表示字符串
C语言中表示字符串,最常用的是ASCII码
字符串的内容与字节顺序和字大小规则,无关,文本数据比二进制数据具有更强的平台独立性
//ASCII码适合英文,Unicode则包罗万象,C语言也有支持unicode的程序库
2.1.5 表示代码
二进制代码是不兼容的,可移植性较低
2.1.6 布尔代数简介
1850年前后,乔治·布尔(George Boole)注意到通过将逻辑值TRUE和FALSE编码为二进制值1和0,能够设计出一种代数,布尔代数(Boolean algebra),以研究逻辑推理的基本原则
布尔运算可以拓展到位向量的运算
&, |, ^
2.1.7 C语言中的位级运算
位级运算的一个常见用法就是实现掩码运算
//除了x的最低有效字节外,其他的位都取补,最低有效字节保持不变:x^~0xFF
2.1.8 C语言中的逻辑运算
2.1.9 C语言中的移位运算
实际上,几乎所有编译器/机器组合都对有符号数使用算数右移
对于无符号数,右移必须是逻辑的
//注意,+,-的优先级高于>>,<<
2.2 整数表示
2.2.1 整型数据类型
2.2.2 无符号数的编码
原理:无符号数编码的定义
对向量
x
⃗
=
[
x
ω
−
1
,
x
ω
−
2
,
.
.
.
,
x
0
]
\vec{x}=[x_{\omega-1},x_{\omega-2},...,x_0]
x=[xω−1,xω−2,...,x0]
B
2
U
w
(
x
⃗
)
=
.
∑
i
=
0
ω
−
1
x
i
2
i
B2U_w(\vec{x})\overset{.}{=}\sum_{i=0}^{\omega-1}x_i2^i
B2Uw(x)=.i=0∑ω−1xi2i
原理:无符号数编码的唯一性
函数
B
2
U
w
是一个双射
函数B2U_w 是一个双射
函数B2Uw是一个双射
2.2.3 补码编码
原理:有符号数编码的定义
对向量
x
⃗
=
[
x
ω
−
1
,
x
ω
−
2
,
.
.
.
,
x
0
]
\vec{x}=[x_{\omega-1},x_{\omega-2},...,x_0]
x=[xω−1,xω−2,...,x0]
B
2
T
w
(
x
⃗
)
=
.
−
x
ω
−
1
2
ω
−
1
+
∑
i
=
0
ω
−
2
x
i
2
i
B2T_w(\vec{x})\overset{.}{=}-x_{\omega-1}2^{\omega-1}+\sum_{i=0}^{\omega-2}x_i2^i
B2Tw(x)=.−xω−12ω−1+i=0∑ω−2xi2i
原理:补码编码的唯一性
函数
B
2
T
ω
是一个双射
B2T_{\omega}是一个双射
B2Tω是一个双射
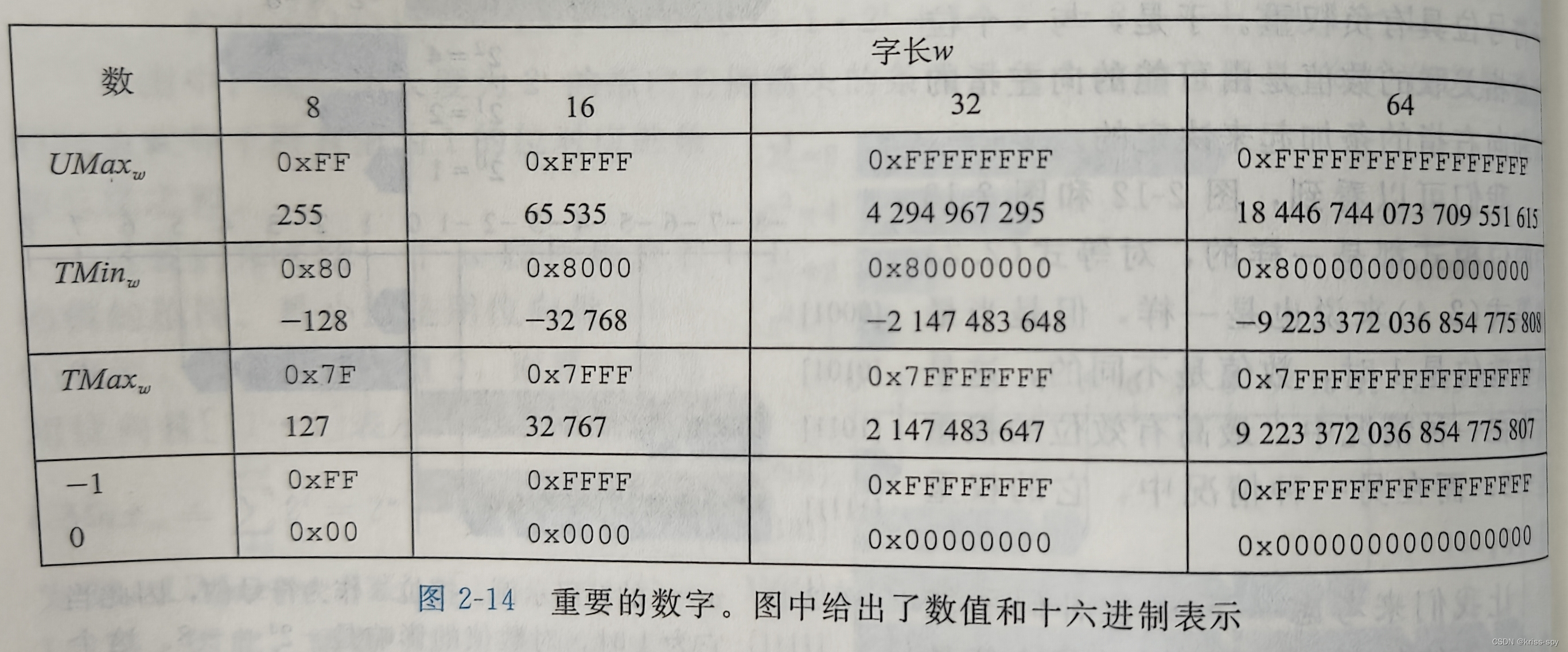
∣
T
M
i
n
∣
=
∣
T
M
a
x
∣
+
1
|TMin|=|TMax|+1
∣TMin∣=∣TMax∣+1,
∣
T
M
i
n
∣
|TMin|
∣TMin∣没有与之对应的正数
∣
U
M
a
x
∣
=
2
∣
T
M
a
x
∣
+
1
|UMax|=2|TMax|+1
∣UMax∣=2∣TMax∣+1
∣
U
M
a
x
∣
+
1
=
2
ω
|UMax|+1=2^{\omega}
∣UMax∣+1=2ω
几乎所有的机器都用补码表示有符号整数
printf(”x = %” PRId32 “, y = %” PRIu64 “\n”, x, y);
-> printf(”x = %d, y = %lu\n”, x, y);
2.2.4 有符号数和无符号数之间的转换
对于大多数C语言的实现,强制类型转换都是从位级角度来看的,不一定符合理想的数学规则
强制转换的结果保持位值不变,只是改变了解释这些位的方式
int tu= (int) UMax;
tu == -1;
原理:补码转换为无符号数
对满足
T
M
i
n
ω
≤
x
≥
T
M
a
x
ω
的
x
有
TMin_{\omega}\le x \ge TMax_{\omega}的x有
TMinω≤x≥TMaxω的x有
T
2
U
ω
(
x
)
=
{
x
+
2
ω
x
<
0
x
,
x
≥
0
T2U_{\omega}(x)=\left\{\begin{aligned} & x+2^{\omega}&x<0\\ & x,&x\ge 0\\ \end{aligned}\right.
T2Uω(x)={x+2ωx,x<0x≥0

2.2.5 C语言中的有符号数与无符号数
创建无符号常量要加上后缀U或u,例如12345u
显式转换:tx = (int) ux;
隐式转换:tx = ux;
printf("x = %d = %u", x, x);合法,但可能非直观
执行一个双目运算时,如果一个是有符号,另一个是无符号,C语言会隐式地将有符号参数强制转换为无符号,并假设这两个数都是非负的,例如
-1 < 0U == FALSE
2.2.6 扩展一个数字的位表示
从一个较小的数据类型转换到一个较大的类型,应该总是可能的
无符号数,零扩展(zero extension)
有符号数,符号拓展(sign extension)
2.2.7 截断数字
截断无符号数:
x
′
⃗
是将
x
⃗
截断为
k
为的结果
\vec{x'}是将\vec{x}截断为k为的结果
x′是将x截断为k为的结果
x
=
B
2
U
ω
(
x
⃗
)
,
x
′
=
B
2
U
k
(
x
′
⃗
)
x=B2U_{\omega}(\vec{x}),\,x'=B2U_{k}(\vec{x'})
x=B2Uω(x),x′=B2Uk(x′)
则
x
′
=
x
m
o
d
2
k
则x'=x\,mod\,2^k
则x′=xmod2k
截断补码数值:
x
′
⃗
是将
x
⃗
截断为
k
为的结果
\vec{x'}是将\vec{x}截断为k为的结果
x′是将x截断为k为的结果
x
=
B
2
T
ω
(
x
⃗
)
,
x
′
=
B
2
T
k
(
x
′
⃗
)
x=B2T_{\omega}(\vec{x}),\,x'=B2T_{k}(\vec{x'})
x=B2Tω(x),x′=B2Tk(x′)
则
x
′
=
U
2
T
k
(
x
m
o
d
2
k
)
则x'=U2T_k\,(x\,mod\,2^k)
则x′=U2Tk(xmod2k)
2.2.8 关于有符号数和无符号数的建议
有符号数到无符号数的隐式强制类型转换导致了某些非直观行为,它导致的错误很难发现,需要警惕
/*strlen() is size_t, and size_t is unsigned int*/
/*This function is buggy*/
int strlonger(char*s, char*t)
{
return strlen(s)-strlen(t) >0;
}
2.3 整数运算
2.3.1 无符号加法
原理:无符号数的加法
x
+
ω
u
y
=
{
x
+
y
,
x
+
y
<
2
ω
正常
x
+
y
−
2
ω
,
2
ω
≤
x
+
y
<
2
ω
+
1
溢出
x+_\omega^u y=\left\{\begin{aligned} & x+y, && x+y<2^\omega &正常\\ & x+y-2^\omega, && 2^\omega \le x+y<2^{\omega+1} &溢出\\ \end{aligned}\right.
x+ωuy={x+y,x+y−2ω,x+y<2ω2ω≤x+y<2ω+1正常溢出
溢出的结果小于任一所加数,可以用来检测溢出
原理:无符号数求反
−
ω
u
x
=
{
x
,
x
=
0
2
ω
−
x
x
>
0
-^u_{\omega}x=\left\{\begin{aligned} &x,&x=0 \\ &2^\omega-x&x>0 \\ \end{aligned}\right.
−ωux={x,2ω−xx=0x>0
2.3.2 补码加法
原理:补码加法
x
+
ω
t
y
=
{
x
+
y
−
2
ω
,
2
ω
≤
x
+
y
正溢出
x
+
y
,
−
2
ω
−
1
≤
x
+
y
<
2
ω
正常
x
+
y
+
2
ω
,
x
+
y
<
−
2
ω
−
1
负溢出
x+^t_\omega y=\left\{\begin{aligned} & x+y-2^\omega,&&2^\omega\le x+y &&正溢出\\ & x+y,&&-2^{\omega-1}\le x+y<2^\omega &&正常\\ & x+y+2^\omega,&&x+y<-2^{\omega-1} &&负溢出\\ \end{aligned}\right.
x+ωty=⎩
⎨
⎧x+y−2ω,x+y,x+y+2ω,2ω≤x+y−2ω−1≤x+y<2ωx+y<−2ω−1正溢出正常负溢出
无论是否溢出,x+y-x==y
2.3.3 补码的非
原理:补码的非
−
ω
t
x
=
{
T
M
i
n
ω
,
x
=
T
M
i
n
ω
−
x
,
x
>
T
M
i
n
ω
-^t_{\omega}x=\left\{\begin{aligned} & TMin_{\omega},&x=TMin_{\omega}\\ & -x,&x>TMin_{\omega}\\ \end{aligned}\right.
−ωtx={TMinω,−x,x=TMinωx>TMinω
2.3.4 无符号乘法
原理:无符号数乘法
x
∗
ω
u
y
=
(
x
⋅
y
)
m
o
d
2
ω
x*^u_{\omega}y=(x\cdot y)\,mod\,2^{\omega}
x∗ωuy=(x⋅y)mod2ω
2.3.5 补码乘法
原理:补码乘法
x
∗
ω
t
y
=
U
2
T
ω
(
(
x
⋅
y
)
m
o
d
2
ω
)
x*^t_{\omega}y=U2T_{\omega}((x\cdot y)\,mod\,2^{\omega})
x∗ωty=U2Tω((x⋅y)mod2ω)
原理:无符号和补码乘法的位级等价性
x
=
B
2
T
ω
(
x
⃗
)
,
y
=
B
2
T
ω
(
y
⃗
)
x=B2T_{\omega}(\vec{x}),y=B2T_{\omega}(\vec{y})
x=B2Tω(x),y=B2Tω(y)
x
′
=
B
2
U
ω
(
x
⃗
)
,
y
=
B
2
U
ω
(
y
⃗
)
x'=B2U_{\omega}(\vec{x}),y=B2U_{\omega}(\vec{y})
x′=B2Uω(x),y=B2Uω(y)
则
T
2
B
ω
(
x
∗
ω
t
y
)
=
U
2
B
ω
(
x
′
∗
ω
u
y
′
)
则T2B_{\omega}(x*^{t}_{\omega}y)=U2B_{\omega}(x'*^u_{\omega}y')
则T2Bω(x∗ωty)=U2Bω(x′∗ωuy′)
2.3.6 乘以常数
由于整数乘法比移位和加法的代价要大得多,许多C编译器试图以移位,加法和减法的组合来消除很多整数乘以常数的情况
x * 14 ==> (x<<3) + (x<<2) + (x<<1)
2.3.7 除以2的幂
同理,除以2的幂也可以用右移运算来实现
2.3.8 关于整数运算的最后思考
计算机执行的“整数运算“,实际上是一种模运算形式
结果运算可能溢出
无符号形式和补码形式的运算数,都有完全一样或者非常类似的位级行为
2.4 浮点数
上世纪80年代,IEEE浮点标准统一了不同的浮点数标准
2.4.1 二进制小数
由于二进制编码的限制,除了0.5这样的数,小数无法被真正精确地表示
例如,
0.111...
1
2
0.111...1_2
0.111...12表示的是刚好小于1的数
2.4.2 IEEE浮点表示
IEEE浮点标准用
V
=
(
−
1
)
s
×
M
×
2
E
V=(-1)^s \times M \times 2^E
V=(−1)s×M×2E的形式来表示一个数
符号(sign)s,尾数(significand)M,阶码(exponent)E
C语言float,32位,1+8+23
C语言double,64位,1+11+52

+0.0和-0.0
NaN(not a number)
2.4.3 数字示例
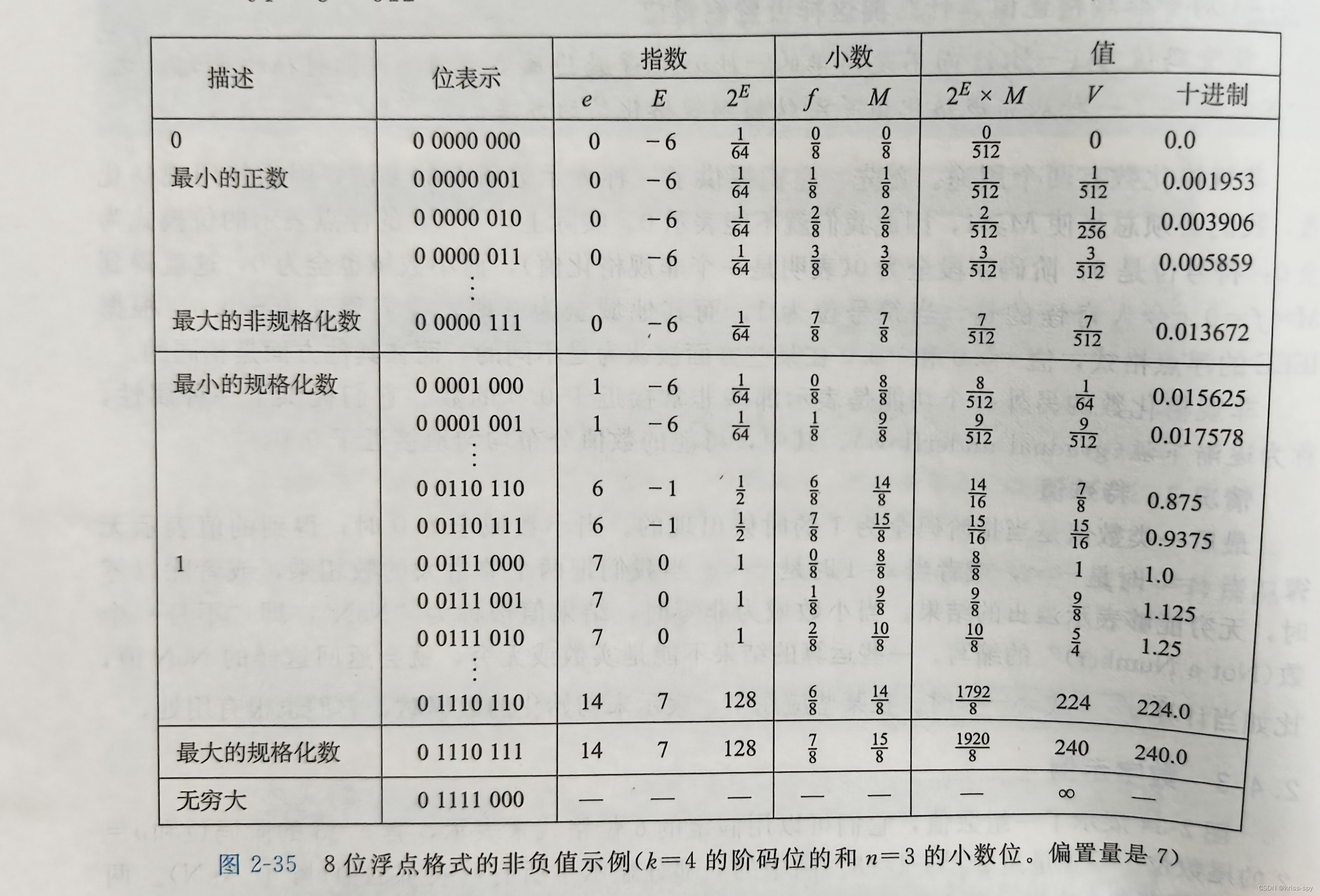
2.4.4 舍入
舍入(rounding)运算的任务,是用一种系统的方法,找到最接近x的,可以用浮点形式表示的x’
向偶数舍入(round-to=even),也被称为向最接近的值舍入(round-to-neareset),是默认的方式
2.4.5 浮点运算
浮点加法不具有结合性
3.14+1e10-1e10 == 0
3.14+(1e10-1e10) == 3.14
浮点加法不具备分配性
1e20*(1e20-1e20) == 0.0
1e20*1e20-1e20*1e20 == NaN
2.4.6 C语言中的浮点数
C语言标准不要求机器使用IEEE标准
C语言中浮点数转换为整数,有较多潜在问题
//将大的浮点数转换为整数是一种常见的程序错误来源,它曾直接导致Ariane 5火箭解体爆炸
2.5 小结
计算机将信息编码为位,通常组织成字节序列
有不同的编码方式用来表示整数、实数和字符串
不同的计算机模型在编码数字和多字节数据中的字节顺序是使用不同的约定
大多数机器对整数使用补码编码,对浮点数使用IEEE标准754编码
从位级上理解编码和运算,对于程序的数据灵活性十分重要
注意C语言的溢出
浮点运算只有有限的范围和精度,而且并不遵守普遍的算术属性,必须小心使用

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








