蓝桥杯备考：背包问题之Shaass 和书架

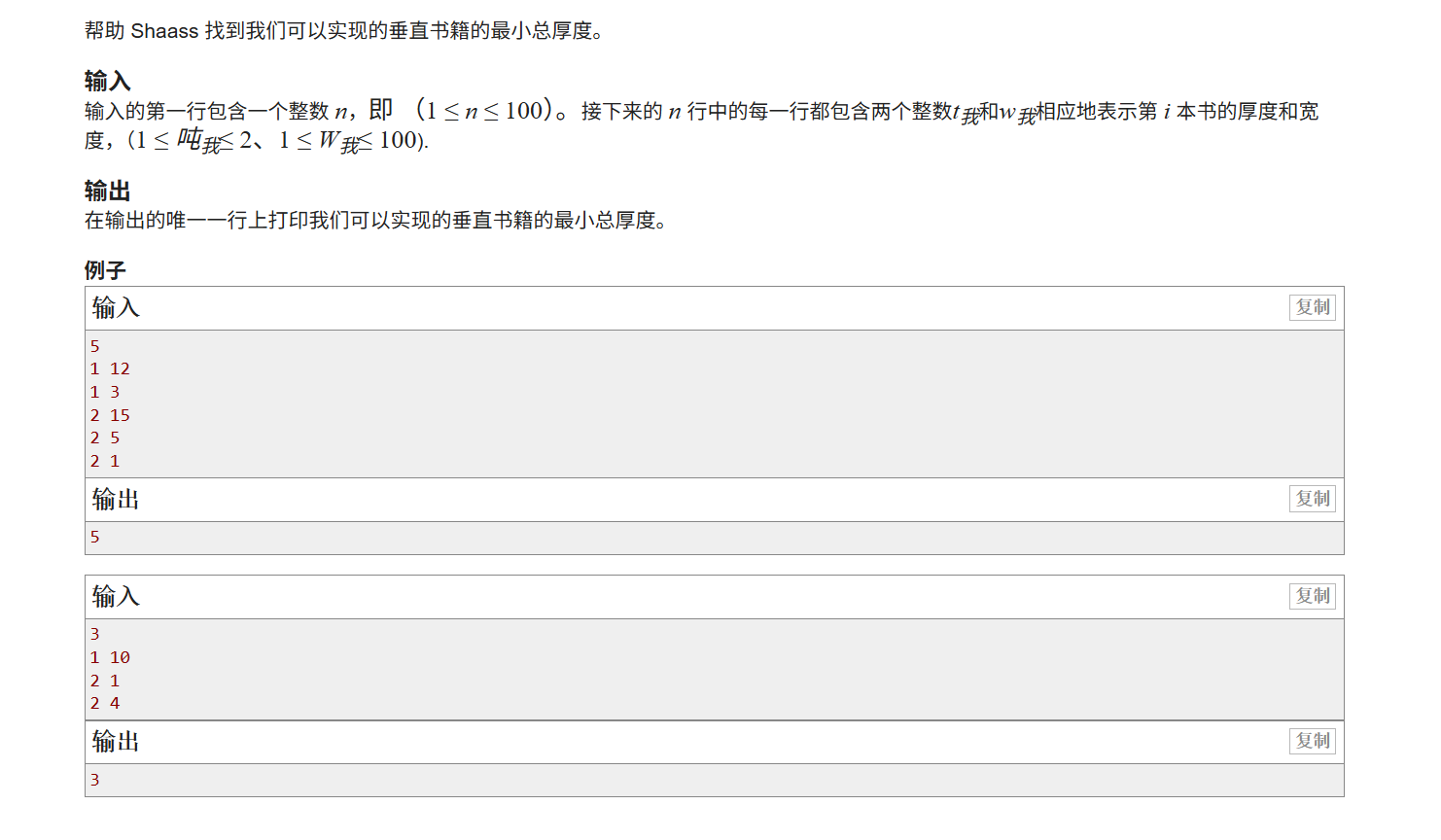
我们可以先求上面放置的书的最小宽度，

1.确定状态表示 

f[i][j]表示从1到i本书里面选出总厚度为j的书放在上面

2.推导状态转移方程

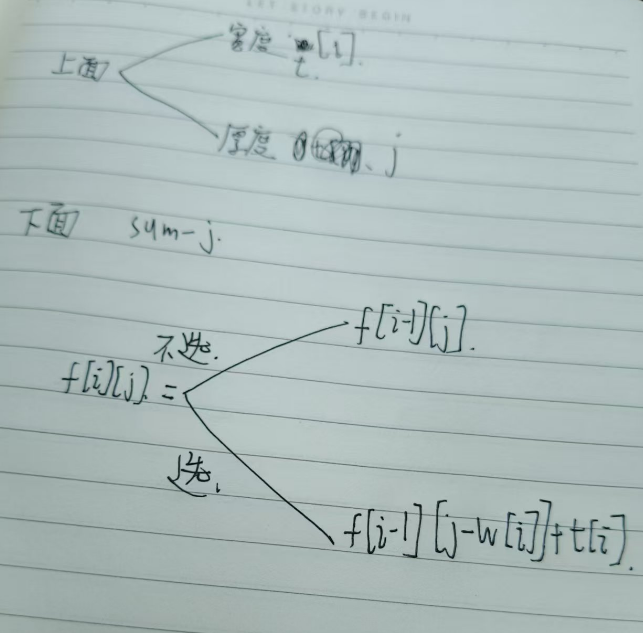
step3:初始化

全部初始化为0x3f3f3f3f，f[0][0]初始化为0

step4:确定 填表顺序

应当是从上到下，优化成一维应该从右到左

step5:结果

结果存储在f[n][j]里面，j是上面书的厚度，j越小，宽度越大，j越大，宽度越小，我们从大到小枚举j，如果有满足题目要求的，直接输出然后break

下面实现代码

#include <iostream>
#include <cstring>
using namespace std;
const int N = 110,M= 510;
int n;
int w[N],t[N];
int f[M];
int main()
{
	cin >> n;
	int sum = 0;
	for(int i = 1;i<=n;i++)
	{
		cin >> t[i] >> w[i];
		sum+=t[i];
	}
	memset(f,0x3f,sizeof f);
	f[0] = 0;
 	for(int i = 1;i<=n;i++)
	{
		for(int j = sum;j>=t[i];j--)
		{
			f[j] = min(f[j],f[j-t[i]]+w[i]);
		}
	}
	for(int j = sum;j>=0;j--)
	{
		if(f[j]<=sum-j)
		{
			cout << sum-j;
			return 0;
		}
	}
	
	
	
	
	
	return 0;
}