排序算法
前言
排序在我们生活中处处可见,例如在考完试后通过成绩划分排名的高低,军训时按身高的高矮战队,打扑克牌时摆牌的顺序等,这些场景都会用到排序。而在我们的计算机中也会使用排序算法堆数据进行比较,接下来就和小编一起用C语言来实现一些计算机中常见的排序把。
1.排序的分类
常见的排序分为四类:插入排序、选择排序、交换排序、归并排序。
(1)插入排序:直接插入排序、希尔排序。
(2)选择排序:直接选择排序、堆排序。
(3)交换排序:冒泡排序、快速排序。
(4)归并排序:归并排序。
2.直接插入排序
<1>直接插入排序算法思想
直接插入排序的算法思想是把待排序数组中的最前面的值插入到有序数组,直到没有待排的数据,我们平时打扑克牌不停地拿牌给扑克牌排序就是利用了类似的思想。
<2>直接插入排序动图演示

<3>直接插入排序的代码演示
//直接插入排序
void InitSort(int* arr, int n)
{
for (int i = 0; i < n - 1; i++)
{
int end = i;
int tmp = arr[end + 1];
//将待排序的元素插入到有序元素中
while (end >= 0)
{
if (arr[end] > tmp)
{
arr[end + 1] = arr[end];
end--;
}
else
{
break;
}
}
arr[end + 1] = tmp;
}
}
<4>直接插入排序时间复杂度与空间复杂度以及稳定性
(1)时间复杂度:o(n^2)。
(2)空间复杂度:o(1)。
(3)稳定性: 稳定。
<5>直接插入排序的注意事项
逆序的时候时间复杂度最差,一般不会用这种情况。
3.希尔排序
<1>希尔排序的算法思想
希尔排序的算法思想是把 一套数据换分成若干组数据,然后对每一组数据进行直接插入排序,然后再划分成若干组进行直接插入排序,直到最后所有数据化分为一组然后在进行直接插入排序(每次分的组都要比前一次每组元素个数要少)。
<2>希尔排序动图演示

<3>希尔排序的代码演示
//希尔排序
void ShellSort(int* arr, int n)
{
int gap = n;
while (gap > 1)
{
//把数据分为gap组,+1是因为要保证最后一次的gap值必须为1。
gap = gap / 3 + 1;
//开始对每组数据进行直接插入排序,需要注意end加或减的值
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = arr[end + gap];
while (end >= 0)
{
if (arr[end] > tmp)
{
arr[end + gap] = arr[end];
end -= gap;
}
else
{
break;
}
}
arr[end + gap] = tmp;
}
}
}
<4>希尔排序的时间复杂度与空间复杂度以及稳定性
(1)时间复杂度:o(n^1.3)。
(2)空间复杂度:o(1)。
(3)稳定性:不稳定。
<5>希尔排序的注意事项
(1)直接插入排序相当于选择排序的优化,把数据划分为多组组进行直接插入排序大大减少了数据需要移动的步数。
(2)组数也不是分的越多越好这里小编推荐每次除以三,不要问为什么。
(3)希尔排序的时间复杂度现在仍然是数学界的一大难题,不必去深究,记住就行。
4.直接选择排序
<1>直接选择排序的算法思想
直接选择排序的算法思想是遍历待排数据,将其中最小的值放到最前该段待排数据的最前面。
<2>直接选择排序动图演示
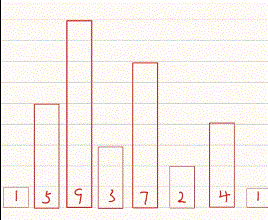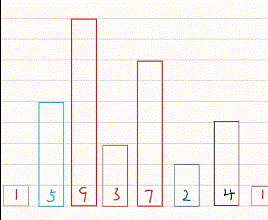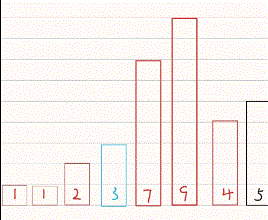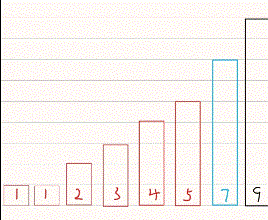
<3>直接选择排序代码演示
//直接选择排序
void SelectSort(int* arr, int n)
{
for (int i = 0; i < n - 1; i++)
{
int min = i;
for (int j = i + 1; j < n; j++)
{
if (arr[j] < arr[min])
{
min = j;
}
}
swap(&arr[i], &arr[min]);
}
}
<4>直接选择排序代码优化
//直接选择排序优化
void SelectSort1(int* arr, int n)
{
int begin = 0;
int end = n - 1;
while (begin < end)
{
int min = begin;
int max = begin;
for (int i = begin; i <= end; i++)
{
if (arr[min] > arr[i])
{
min = i;
}
if (arr[max] < arr[i])
{
max = i;
}
}
swap(&arr[min], &arr[begin]);
if (max == begin)
{
max = min;
}
swap(&arr[max], &arr[end]);
begin++;
end--;
}
}
<5>直接选择排序时间复杂度空间复杂度以及稳定性
(1)时间复杂度:o(n^2)。
(2)空间复杂度:o(1)。
(3)稳定性:不稳定。
<6>直接选择排序的注意事项
(1)代码优化是每次遍历找出最大值和最小值分别放在两边。
(2)不管什么情况直接选择排序时间复杂度的情况都是一样的不存在最好和最坏的区分。
5.堆排序
<1>堆排序的算法思想
堆排序的算法思想是吧堆顶的数据与堆尾的数据进行交换,然后减小堆的长度,利用向下调整建堆或者向上调整建堆,继续调整堆顶的数据,然后重复前面的步骤,直到堆的大小为1,至此排序完成,输出数组即可完成排序。
<2>堆排序的动图演示
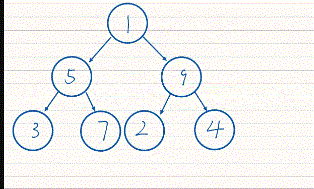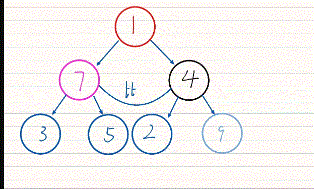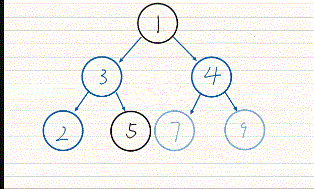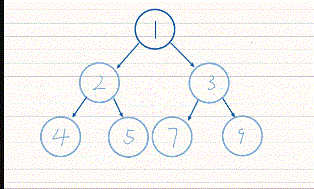
<3>堆排序的向上调整建堆代码演示
//向上调整建堆
void ADjustUp(int* arr, int child)
{
int prent = (child - 1) / 2;
while (child > 0)
{
if (arr[child] > arr[prent])
{
swap(&arr[child], &arr[prent]);
child = prent;
prent = (child - 1) / 2;
}
else
{
break;
}
}
}
<4>堆排序的向下调整建堆代码演示
//向下调整建堆
void ADjustDown(int* arr, int prent, int n)
{
int child = 2 * prent + 1;
while (child < n)
{
if (child + 1 < n && arr[child] < arr[child + 1])
{
child++;
}
if (arr[child] > arr[prent])
{
swap(&arr[prent], &arr[child]);
prent = child;
child = prent * 2 + 1;
}
else
{
break;
}
}
}
<5>堆排序代码演示
//堆排序
void HeapSort(int* arr, int n)
{
int end = n - 1;
for (int i = (end - 1) / 2; i >= 0; i--)
{
ADjustDown(arr, i, n);
}
while (end > 0)
{
swap(&arr[0], &arr[end]);
ADjustDown(arr, 0, end);
end--;
}
}
<6>堆排序的时间复杂度空间复杂度以及稳定性
(1)时间复杂度:o(N*logN)。
(2)空间复杂度:o(1)。
(3)稳定性:不稳定。
<7>堆排序的注意事项
(1)由于向下调整建堆优于向上调整建堆,因此本文所用的都是向下调整建堆的思想。
(2)升序:建大根堆;降序:建小根堆。
(3)孩结点子找双亲结点:prent = (child - 1) / 2;
双结点亲找孩子结点:child = prent * 2 + 1; child < n
child = prent * 2 + 2; child < n
(4)向下调整建堆:前提是除了堆顶其他的子树都必须构成堆,然后从堆顶开始向下比较数据,将最大或最小移动到最上面,直到孩子结点大于或等于堆的个数,从而构成一个新堆。
(5)向上调整建堆:前提是去掉堆尾的数据必须构成一个堆,利用子节点寻找父亲结点,然后比较大小交换,直到结点小于或等于0,从而构成一个新的堆。
(6)堆排序必须是一颗完全二叉树。
6.冒泡排序
<1>冒泡排序的算法思想
冒泡排序的算法思想是多次遍历数组,从头开始比较,如果该数据大于或者小于后一个数据则交换,并且指向该数据的下标加一,否则不用交换但下标依旧加一,这样每次循环就可以把最大的数据排到末尾,循环n-1次就可以排完全部数据。
<2>冒泡排序的动图演示

<3>冒泡排序的代码演示
//冒泡排序
void BubbleSort(int* arr, int n)
{
for (int i = 0; i < n - 1; i++)
{
int index = 0;
//注
for (int j = 0; j < n - i - 1; j++)
{
if (arr[j] > arr[j + 1])
{
index = 1;
swap(&arr[j], &arr[j + 1]);
}
}
if (index == 0)
{
break;
}
}
}
<4>冒泡排序的时间复杂度与空间复杂度以及稳定性
(1)时间复杂度:o(n^2)。
(2)空间复杂度:o(1)。
(3)稳定性:稳定。
<5>冒泡排序的注意事项
(1)冒泡排序效率非常低,只用于教学。
7.快速排序
<1>快速排序的算法思想
快速排序的算法思想是,利用基准值,划分出段区间在区间中继续找基准值划分下去,直到不可划分为止,找基准值我们有三种方法:hoare版本找基准值、挖坑法、双指针法。
<2>快速排序找基准值的动图演示
注:这里找基准值的方法都是单趟演示
(1)hoare版本

(2)挖坑法

(3)双指针法
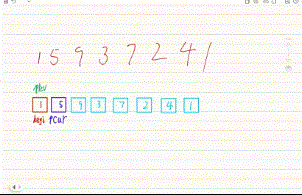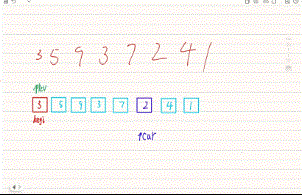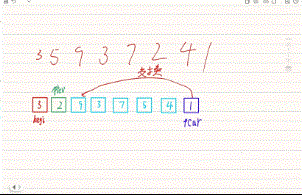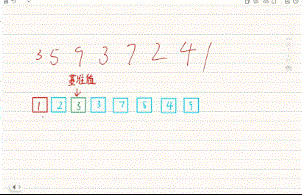
<3>快速排序的代码演示
(1)hoare版本代码
int _QuickSort1(int* arr, int left, int right)
{
int keyi = left;
left++;
while (left <= right)
{
while (left <= right && arr[right] > arr[keyi])
{
right--;
}
while (left <= right && arr[left] < arr[keyi])
{
left++;
}
if (left <= right)
{
swap(&arr[left++], &arr[right--]);
}
}
swap(&arr[right], &arr[keyi]);
return right;
}
(2)挖坑法代码
//挖坑法找基准值
int _QuickSort2(int* arr, int left, int right)
{
int tmp = arr[left];
int hore = left;
while (left < right)
{
while (left < right && arr[right] >= tmp)
{
right--;
}
arr[hore] = arr[right];
hore = right;
while (left < right && arr[left] <= tmp)
{
left++;
}
arr[hore] = arr[left];
hore = left;
}
arr[hore] = tmp;
return hore;
}
(3)双指针法代码
//双指针法找基准值
int _QuickSort3(int* arr, int left, int right)
{
int prev = left;
int pcur = prev + 1;
while (pcur <= right)
{
//注
if (arr[pcur] < arr[left] && ++prev != pcur)
{
swap(&arr[prev], &arr[pcur]);
}
pcur++;
}
swap(&arr[left], &arr[prev]);
return prev;
}
(4)快排代码
//快速排序
void QuickSort1(int* arr, int left, int right)
{
if (left >= right)
{
return;
}
int key = _QuickSort3(arr, left, right);
QuickSort1(arr, left, key - 1);
QuickSort1(arr, key + 1, right);
}
(5)快排非递归版本
注:需要借助栈
//非递归版本的快速排序
void QuickSort2(int* arr, int left,int right)
{
//注意统一栈的判空标准
ST st;
STInit(&st);
StackPush(&st, right);
StackPush(&st, left);
while (!StackEmpty(&st))
{
int begin = StackFront(&st);
StackPop(&st);
int end = StackFront(&st);
StackPop(&st);
int keyi = _QuickSort3(arr, begin, end);
int begin1 = begin, end1 = keyi - 1;
int begin2 = keyi + 1, end2 = end;
if (begin2 < end2)
{
StackPush(&st, end2);
StackPush(&st, begin2);
}
if (begin1 < end1)
{
StackPush(&st, end1);
StackPush(&st, begin1);
}
}
STDestroy(&st);
}
<4>快速排序的时间复杂度与空间复杂度以及稳定性
(1)时间复杂度:o(N*logN)。
(2)空间复杂度:o(logN)。
(3)稳定性:不稳定。
<5>快速排序的注意事项
(1)快速排序是一种效率非常高的排序,需要重点掌握。
(2)快排的非递归版本比递归版更为使用,不会有栈溢出的风险,但要借助栈数据结构要实现,手搓栈的代码还是有点麻烦的。
(3)本文快速排序找基准值的方法并不完善,还有三路区中等方法可以优化,小编会在以后的文章中更新,请大家持续关注。
8.归并排序
<1>归并排序算法思想
归并排序采用了分治的算法思想,把数组区间分成左右两块,类似于二叉树的左子树和右子树,左子树和右子树又可以再分,一直分到不能分割,然后然后开始合并,合并的步骤为两个有序区间合并为一个有序区间。
<2>归并排序动图
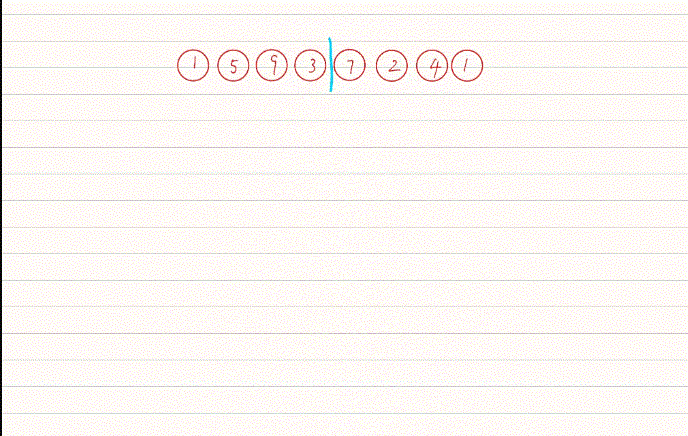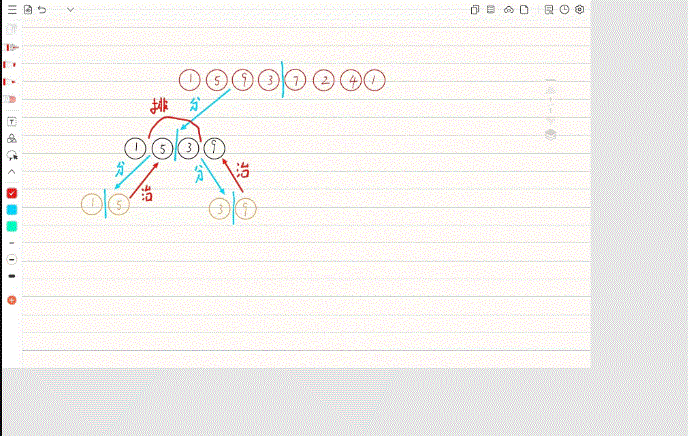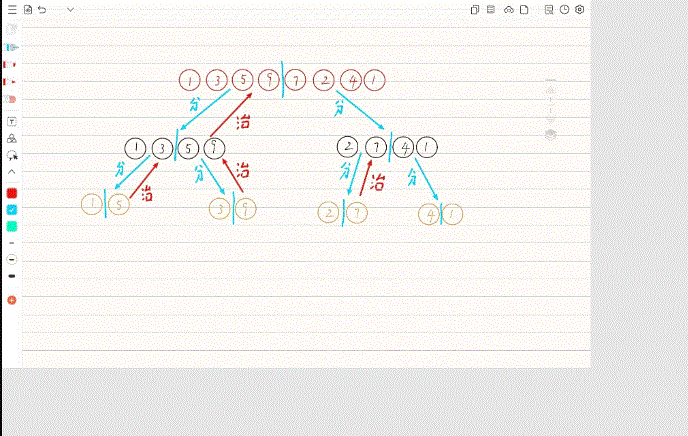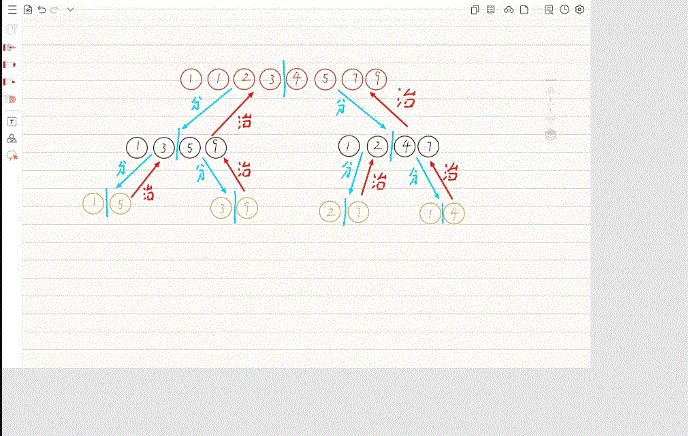
<3>归并排序的代码演示
//归并排序(子)
void _mergeSort(int* arr, int left, int right, int* tmp)
{
if (left >= right)
{
return;
}
int keyi = (left + right) / 2;
_mergeSort(arr, left, keyi, tmp);
_mergeSort(arr, keyi + 1, right, tmp);
int begin1 = left, end1 = keyi;
int begin2 = keyi + 1, end2 = right;
int index = left;
while(begin1<=end1 && begin2 <= end2)
{
//注意复制数组
if (arr[begin1] < arr[begin2])
{
tmp[index++] = arr[begin1++];
}
else
{
tmp[index++] = arr[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = arr[begin2++];
}
for (int i = left; i <= right; i++)
{
arr[i] = tmp[i];
}
}
//归并排序
void mergeSort(int* arr, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
exit(-1);
}
_mergeSort(arr, 0, n - 1, tmp);
free(tmp);
tmp = NULL;
}
<4>归并排序的时间复杂度与空间复杂度以及稳定性
(1)时间复杂度:o(N*logN)。
(2)空间复杂度:o(N)。
(3)稳定性:稳定。
<5>归并排序的注意事项
(1)这里归并排序的动图省略了数组复制,和两数组合并的步骤需要注意。
(2)采用了分支的思想,类似于二叉树。
8.计数排序(适用于部分类型)
<1>计数排序的算法的思想
计数排序的算法思想,是利用数字的出现次数和数字的数字与数组下标的关系而排序的,是一种不用比较的线性的算法思想。
<2>计数排序的代码演示
//计数排序
void CountSort(int* arr, int n)
{
int max = arr[0], min = arr[0];
for (int i = 1; i < n; i++)
{
if (max < arr[i])
{
max = arr[i];
}
if (min > arr[i])
{
min = arr[i];
}
}
int rang = max - min + 1;
int* tmp = (int*)calloc(rang,sizeof(int));
if (tmp == NULL)
{
exit(-1);
}
for (int i = 0; i < n; i++)
{
tmp[arr[i] - min]++;
}
int index = 0;
//数组的小于条件
for (int i = 0; i < rang; i++)
{
while (tmp[i]--)
{
arr[index] = i + min;
index++;
}
}
free(tmp);
tmp = NULL;
}
<3>计数排序的时间复杂度空间复杂度以及稳定性
(1)时间复杂度:o((N+范围)
(2)空间复杂度:o(范围)
(3)稳定性:稳定。
<4>计数排序的注意事项
(1)计数排序只适用于整数。
(2)计数排序不能存在大于或等于整形范围的数组,不然数组下标会越界。
(3)计数排序对于数据集中的排序效率特别高,若数据较为分散则不建议使用计数排序。
总结
这里对于基本的排序类型就讲解完毕,今后也会不定期的更新其它排序,如果大家觉得小编的文章开门(有货)的话留个赞再走吧,下期见,拜拜~~~





















 1万+
1万+










