Codeforces Round 1006 (Div. 3) A-G 题解

xinxin-gg

已于 2025-02-27 18:43:22 修改

阅读量1.7k

点赞数 40

CC 4.0 BY-SA版权

分类专栏： codeforces 文章标签： c++ 算法

于 2025-02-26 13:47:50 首次发布

本文链接：https://blog.youkuaiyun.com/2301_81346065/article/details/145875394

codeforces 专栏收录该内容

1 篇文章

订阅专栏

做题情况：

A. New World, New Me, New Array

模拟+贪心

题意：给一个有 $n$ 个全 $0$ 元素的数组,可以将任一元素修改为 $[-p,p]$ ，求最少操作次数使得数组元素总和为 $k$ 。

思路：每一个数都尽可能改成 $p$ ，符号与 $k$ 相同即可。如果全部元素都改完还不行即 $np<\left | k \right |$ 就输出-1。

时间复杂度： $O(1)$

代码如下：

#include<bits/stdc++.h>
using namespace std;

void solve(){
	int n,k,p;
	cin>>n>>k>>p;
	int res=abs(k)/p;
	if(abs(k)%p) res+=1;
	if(abs(res)>n) cout<<"-1"<<endl;
	else
		cout<<res<<endl;
}

signed main(void){
	ios::sync_with_stdio(false);
	cin.tie(nullptr),cout.tie(nullptr);
	int t;
	cin>>t;
	while(t--)
		solve();
	return 0;
}

B. Having Been a Treasurer in the Past, I Help Goblins Deceive

模拟

题意：给一个字符串，任意重排这个字符串，输出字串哥布林脸的最大个数，哥布林的脸如
$-_--$ 。

思路：把’-‘对称的放在两边，’_'放在中间。结果就是 $(\tfrac{N('-')}{2}) *N('\_')*(N('-')-\tfrac{N('-')}{2})$ 。

这里由于 $N('-')$ 固定，利用和一定相同积最大的性质。

时间复杂度： $O(n)$

代码如下：

#include<bits/stdc++.h>
using namespace std;
#define int long long

void solve(){
	int n;
	cin>>n;
	string s;
	cin>>s;
	int num1=0,num2=0;
	for(int i=0;i<n;i++){
		if(s[i]=='-') num1++;
		if(s[i]=='_') num2++;
	}
	int ans=(num1/2)*num2*(num1-(num1/2));
	cout<<ans<<endl;
}

signed main(void){
	ios::sync_with_stdio(false);
	cin.tie(nullptr),cout.tie(nullptr);
	int t;
	cin>>t;
	while(t--)
		solve();
	return 0;
}

C. Creating Keys for StORages Has Become My Main Skill

构造

题意：给定数组长度 $n$ ，要求数组中所有元素或运算之后结果为 $x$ ，定义 $MEX$ ，可以知道 $MEX$ 即从 $i=0$ 开始逐一递增遍历，数组中第一次未出现的数。输出使 $MEX$ 最大的数组。

思路：考虑 $MEX$ 的特性我们只需要从 $i=0$ 开始往数组中填数，每次保证 $x|i==x$ ，因为或运算可以交换顺序，数组中所有元素或运算之后结果为 $x$ 的必要条件为 $x|i==x(\forall i\subset a)$ 。如果一旦不能填数了那么就终止循环，后面全填 $x$ 即可因为 $x|x==x$ 。

需要特别注意的是循环结束条件为 $i<=2x$ $and$ $cnt<n-1$ 。 $i<2x$ 是因为可能存在比 $x$ 大的数也满足 $x|i==x(\forall i\subset a)$ ；留两个数以防所有数组中的数异或不能等于 $x$ ，即保证充分性。

时间复杂度： $O(n)$

代码如下：

#include<bits/stdc++.h>
using namespace std;
#define int long long

void solve(){
	int n,x;
	cin>>n>>x;
	int res=0;
	int cnt=0;	
	int i;
	int before=0;
	for(i=0;i<=2*x && cnt<n-1;i++){
		if((x|i) == x) {
			cnt++;
			cout<<i<<' ';
			res=res|i;
			if(i>1 && (i-before)!=1) break;
			before=i;
		}
		else{
			if(i>1 && (i-before)!=1) break;
			continue;
		}
		
	}
	while(cnt!=n){
		cnt++;
		if((res|i)==x) cout<<i<<' ';
		else
			cout<<x<<' ';
	}
	cout<<endl;
}

signed main(void){
	ios::sync_with_stdio(false);
	cin.tie(nullptr),cout.tie(nullptr);
	int t;
	cin>>t;
	while(t--)
		solve();
	return 0;
}

D. For Wizards, the Exam Is Easy, but I Couldn't Handle It

变相前缀和+贪心

题意：给定长度 $n$ 的数组，要求进行一次操作：对子数组 $[l,r]$ ，将 $a[l]$ 移动到 $a[r]$ 后面。求如何操作才能使原数组逆序对数目尽可能少。

思路：考虑将将 $a[l]$ 移动到 $a[r]$ 后面，如果 $a[l]>a[r]$ ，会增加一组逆序对，如果 $a[l]<a[r]$ ，会减少一组逆序对。用 $cnt$ 记录答案的优劣程度即逆序对减少的个数，越大越优。两次循环即可，分别枚举左边界与右边界，不断维护前缀和 $cnt$ 。

时间复杂度： $O(n^{2})$

代码如下：

#include <bits/stdc++.h>
using namespace std;

int a[2010];

void solve() {
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	
	int best_l = 1, best_r = 1;
	int min_inv=0;
	
	// 枚举所有可能的子数组 [l, r]
	for (int l = 1; l <= n; l++) {
		int inv=0;
		for (int r = l+1; r <= n; r++) {
			if(a[r]>a[l]) inv++;
			if(a[r]<a[l]) inv--;
			if (inv < min_inv) {
				min_inv = inv;
				best_l = l;
				best_r = r;
			}
		}
	}
	cout<<best_l<<' '<<best_r<<endl;
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr), cout.tie(nullptr);
	int t;
	cin>>t;
	while(t--)
		solve();
	return 0;
}

E. Do You Love Your Hero and His Two-Hit Multi-Target Attacks?

数学+贪心

题意：给定 $k$ ,要求在一个平面坐标系输出 $n(0\leqslant n\leqslant 500)$ 个点,使得有 $k$ 组点满足 $\left | x(a)-x(b) \right |+\left |y(a)-y(b) \right |=\sqrt{(x(a)-x(b)^{2})+(y(a)-y(b)^{2})}$ 。

思路：当且仅当两个点在同一行或者同一列，才满足条件 $\left | x(a)-x(b) \right |+\left |y(a)-y(b) \right |=\sqrt{(x(a)-x(b)^{2})+(y(a)-y(b)^{2})}$ 。

一次尽可能多的在同一行放点，如在同一行放了 $m$ 个点，则会为答案贡献 $C\binom{n}{2}$ 。不断模拟尽可能在同一行放即可，放不了去下一行放。需要注意的是不要使这些点在同一列，否则也会增加贡献而且会变得很难想了。由于棋盘足够大边界有 $10^{^{9}}$ ，所以只在行上做文章即可。

时间复杂度： $O(t\sqrt{k})$

代码如下：

#include <bits/stdc++.h>
using namespace std;

// 计算C(n,2)
int C(int n) {
	return n*(n - 1) / 2;
}

void solve() {	
	int k;
	cin >> k;
	vector<int> p;
	int remain=k;
	
	while (remain>0) {
		int n=1;
		while (C(n+1) <= remain) 
			n++;
		p.push_back(n);
		remain -= C(n);
	}
	
	int total=accumulate(p.begin(),p.end(),0);
	cout<<total<<endl;
	
	int x=0;
	for (int i=0; i<p.size(); i++) {
		for (int j=0; j<p[i]; j++) {
			cout<<x<<" "<<i<<endl;
			x++;
		}
	}
}

int main() {
	int t;
	cin >> t;
	while(t--)
		solve();
	return 0;
}

F. Goodbye, Banker Life

数学

lucas、杨辉三角、异或的性质

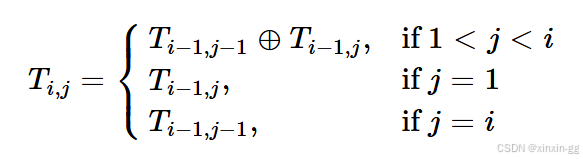
题意：给定满足上述公式的”杨辉三角“，求第 $n$ 行的所有元素，其中每一行首元素和末元素为 $k$ 。

思路：由异或的性质： $x\oplus x=0;x\oplus 0=x$ ，容易知道每一行的元素非 $0$ 即 $k$ ，并且异或操作是加法操作在模2意义上的体现( $0\oplus 0=0;0\oplus 1=1;1\oplus 1=0$ )。

回顾杨辉三角（也叫帕斯卡三角）的性质是： $T_{i,j}=C\binom{i-1}{j-1}$ 。

可以知道对于每一行的中间元素 $T_{i,j}$ ，其等于 $T_{i-1,j}\oplus T_{i-1,j-1}$ 。转换为加法再模2即可。

即 $T_{i,j}=(T_{i-1,j}\oplus T_{i-1,j-1})mod 2 *k = C\binom{i-1}{j-1} mod 2 *k$ 。

由lucas定理 $C\binom{n}{m} mod p =C\binom{nmodp}{mmodp}*C\binom{\left \lfloor n/p \right \rfloor}{\left \lfloor m/p \right \rfloor} mod p$ ，则可以得到 $T_{i,j}$ ，输出每一行的元素即可。

注意：当 $p=2$ 时还有个特别的性质 $C\binom{n}{r} mod 2 = (n \&r == r)$ 。

证明如下：

时间复杂度： $O(nlogn)$

代码如下：

#include <bits/stdc++.h>
using namespace std;

int C(int n,int m){
	int res=1;
	for (int i=m;i>=1;i--) {
		res*=n;
		res/=i;
		n--;
	}
	return res;
}

bool lucus(int n, int k) {
	if(k==0) return 1;
	return ((C(n%2,k%2))*lucus(n/2,k/2))%2;
}

void solve(int n, int k) {
	vector<int> result(n);
	for (int i = 0; i < n; ++i) {
		if (lucus(n-1, i)) 
			result[i] = k;
		else
			result[i] = 0;
	}
	
	for (int i = 0; i < n; ++i) 
		cout << result[i]<<" ";
	cout<<endl;
}

int main() {
	int t;
	cin >> t;
	while (t--) {
		int n, k;
		cin >> n >> k;
		solve(n, k);
	}
	return 0;
}

G. I've Been Flipping Numbers for 300 Years and Calculated the Sum

根号分治整除分块

题意：给定整数 $n$ ，称 $rev(n,p)$ 为 $n$ 在 $p$ 进制下反转后的值。

如6在2进制下为110反转后为011即3， $rev(6,2)=3$ 。现在给定上限 $k$ ，要求 $\sum_{p=2}^{k}rev(n,p)$ 。由于这个值可能非常大，对答案取模 $1e9+7$ 。

思路：题意非常明了，关注数据量 $t=5000$ ， $n=3e5$ ， $k=1e18$ ，显然想到要开 $long long$ 并且时间复杂度要优化到 $O(t\sqrt{n})$ 级别，由于答案是个求和式，显然想到根号分治。

1. 对于 $p\leqslant \sqrt{n}$ 的部分

直接模拟就好, 注意字符串反转即相应位的次放倒过来了。第 $i(0\leqslant i<n)$ 位本来要乘 $p^{i}$ ，现在乘 $p^{n-1-i}$ ，一个循环就可以搞定。如下：

int rev(int n, int p) {
	int res = 0;
	while (n > 0){
		res=res*p+n%p;
		res%=mod;
		n/=p;
	}
	return res;
}

....

for(int p=2;p<=k;p++){
		ans=(ans+rev(n,p))%mod;
	}

2. 对于 $n\geqslant p>\sqrt{n}$ 的部分

可以知道此时 $n$ 在 $p$ 进制下最多只有两位，则 $rev(n,p)=n\%p*p + n/p$ ，但是我们不能直接用这个式子为什么呢？

如果这样模拟 $n\geqslant p>\sqrt{n}$ 的部分，时间复杂度会达到 $O(t\sqrt{n}logn+tn)$ 那么就会TLE了，

~~本人亲测orz。~~

如果对整除分块熟悉的话，利用 $n\%p=n-\left \lfloor \frac{n}{p} \right \rfloor*p$ ，就会想到对上式变形为：

$np-\left \lfloor \frac{n}{p} \right \rfloor*p^{2}+\left \lfloor \frac{n}{p} \right \rfloor$ , 然后把这个式子带入求和项 $\sum_{p=\left \lfloor \sqrt{n} \right \rfloor}^{n}rev(n,p)$ , 得到式子

$\sum_{p=\left \lfloor \sqrt{n} \right \rfloor}^{n}(np-\left \lfloor \frac{n}{p} \right \rfloor*p^{2}+\left \lfloor \frac{n}{p} \right \rfloor )$ 。

然后再利用 $\sum_{l}^{r} i = \frac{(r+l)(r-l+1)}{2}$ 和 $\sum_{l}^{r} i^{2} = \frac{r(r+1)(2r+1)}{6}-\frac{l(l-1)(2l-1)}{6}$ ，将其化简为最简式：

$n\frac{(n+\left \lfloor \sqrt{n} \right \rfloor)(n-\left \lfloor \sqrt{n} \right \rfloor+1)}{2}+\sum_{a_i}^{}(a_i(l_i-r_i+1)-\frac{r(r+1)(2r+1)}{6}+\frac{l(l-1)(2l-1)}{6})$ 。

~~是不是很简单orz~~ 不熟悉整除分块的请去度娘

int sum2(int l,int r) {
	int res=r-l+1;
	return res%mod;
}

int sum3(int x) {
	int res=x*(x+1)*(2*x+1)/6;
	return res%mod;
}

....

if(k>s){
		ans=ans+n*(k+start)%mod*(k-start+1)/2;
		ans%=mod;
		for(int l=start;l<=k;){
			int r=min(n/(n/l),k);
			ans=ans+(n/l)*(sum2(l,r)+2*mod-sum3(r)+sum3(l-1));
			ans%=mod;
			l=r+1;
		}
		k=s;
	}

3. 对于 $p>n$ 的部分

可以知道 $n$ 在 $p$ 进制下反转后还是 $n$ 因为 $n$ 只有一位。答案加上 $(k-n) n$ 即可。

if(k>n) {
		ans+=(k-n)%mod*n%mod;
		k=n;	
	}

需要注意的一个小细节：为了防止溢出，可以将 $mod$ 设置为题目的若干倍，这里我设的 $1e10+70$ 正好是10倍，最后输出 $ans$ 的时候再 $\%(1e9+7)$ 即可，可以避免不必要的麻烦。

~~我就是这样寄了好多次~~

程序跑得飞快~

时间复杂度： $O(t\sqrt{n}logn)$

代码如下：

#include<bits/stdc++.h>
using namespace std;

#define int long long
const int mod=1e10+70;

int rev(int n, int p) {
	int res = 0;
	while (n > 0){
		res=res*p+n%p;
		res%=mod;
		n/=p;
	}
	return res;
}

int sum2(int l,int r) {
	int res=r-l+1;
	return res%mod;
}

int sum3(int x) {
	int res=x*(x+1)*(2*x+1)/6;
	return res%mod;
}

void solve(){
	int n,k;
	cin>>n>>k;
	int ans=0;
	if(k>n) {
		ans+=(k-n)%mod*n%mod;
		k=n;	
	}
	int s=sqrt(n),start=sqrt(n);
	if(s*s<=n) start=s+1;
	if(k>s){
		ans=ans+n*(k+start)%mod*(k-start+1)/2;
		ans%=mod;
		for(int l=start;l<=k;){
			int r=min(n/(n/l),k);
			ans=ans+(n/l)*(sum2(l,r)+2*mod-sum3(r)+sum3(l-1));
			ans%=mod;
			l=r+1;
		}
		k=s;
	}
	for(int p=2;p<=k;p++){
		ans=(ans+rev(n,p))%mod;
	}			
	ans=ans%mod;
	ans=ans%(long long)(1e9+7);
	cout<<ans<<endl;
}

signed main(void){
	ios::sync_with_stdio(false);
	cin.tie(nullptr),cout.tie(nullptr);
	int t;
	cin>>t;
	while(t--)
		solve();
	return 0;
}