艾里 - 贝塞尔子弹（Airy-Bessel bullet）

一、艾里 - 贝塞尔子弹的形成原理

艾里 - 贝塞尔子弹的产生源于复杂的波动光学原理。它通常是在特定的光学系统中，通过对光的振幅、相位和偏振等参量进行精确调控而形成的。从数学角度来看，其光场分布可以用艾里函数和贝塞尔函数的组合来描述，这两种函数在光学领域有着独特的性质，它们的交织使得光场在空间和时间上呈现出高度局域化且稳定传播的特性，宛如一颗飞行的 “子弹” 轨迹，故得名艾里 - 贝塞尔子弹。

例如，在一些实验装置中，利用空间光调制器（SLM）对激光束进行相位调制，将其变换为具有艾里函数横向分布和贝塞尔函数径向分布的光场结构，在合适的传播介质中，这种特殊结构的光场就能维持其独特的形状并稳定传播，形成艾里 - 贝塞尔子弹的形态。

二、特性

1. 无衍射特性：与普通光束在传播过程中会因衍射而逐渐发散不同，艾里 - 贝塞尔子弹具有显著的无衍射特性。这意味着在相当长的传播距离内，它能够保持其初始的光场分布形态，光斑尺寸几乎不发生明显变化。这种特性使得它在长距离光通信、光学成像等领域具有潜在应用价值，能够有效减少信号传输过程中的能量损失和信息失真。
2. 自加速与自愈合能力：艾里 - 贝塞尔子弹具有自加速特性，其传播路径并非直线，而是呈现出一定的弯曲轨迹，并且能够在障碍物或干扰存在的情况下实现自愈合。当它遇到障碍物时，部分光场被遮挡，但在经过障碍物后，光场能够迅速恢复其原有的艾里 - 贝塞尔子弹形态，继续稳定传播，仿佛具有 “生命” 一般能够自我修复，这为其在复杂环境下的光学操控和应用提供了极大的优势。
3. 高能量密度局域化：光场能量高度集中在子弹状的区域内，形成高能量密度的局域化分布。这种特性在诸如激光加工、粒子操控等领域具有重要意义，能够实现对微小目标的高精度、高强度作用，比如可以更精准地对微观生物样本进行光学捕获和操控，或者在超精细的材料加工中实现纳米级别的精准刻蚀和改性。

三、应用领域

1. 光学微操控领域：凭借其高能量密度局域化和自愈合特性，艾里 - 贝塞尔子弹可以用于精确地捕获和操控微小粒子，如生物细胞、纳米颗粒等。在生物医学研究中，能够对细胞进行无损的操控和运输，为细胞生物学研究、基因治疗等提供了一种新的精准操作工具，有助于深入探索细胞内部的奥秘和实现靶向治疗。
2. 光通信领域：其无衍射特性可被应用于构建新型的光通信信道，能够在长距离传输中保持信号的强度和完整性，提高通信容量和质量，减少信号中继的需求，为未来高速、大容量光通信网络的发展提供了新的技术途径，有望突破现有通信技术的带宽限制，满足日益增长的数据传输需求。
3. 激光加工领域：在材料加工方面，艾里 - 贝塞尔子弹的高能量密度局域化使其能够实现对材料的高精度、低损伤加工。例如在半导体芯片制造中，可以对微小的电路结构进行精细雕刻和修整，提高芯片的性能和集成度；在微纳制造领域，能够制造出具有特殊结构和性能的微纳器件，推动微纳技术的发展和应用。

艾里 - 贝塞尔子弹作为光学领域中一种独特而神奇的现象，正逐渐揭开其神秘的面纱，为众多学科和技术领域带来新的机遇和变革，随着研究的不断深入，其必将在更多领域展现出巨大的潜力和价值，推动人类科技的不断进步.

对应的光场表达式

 

 

 

 

 

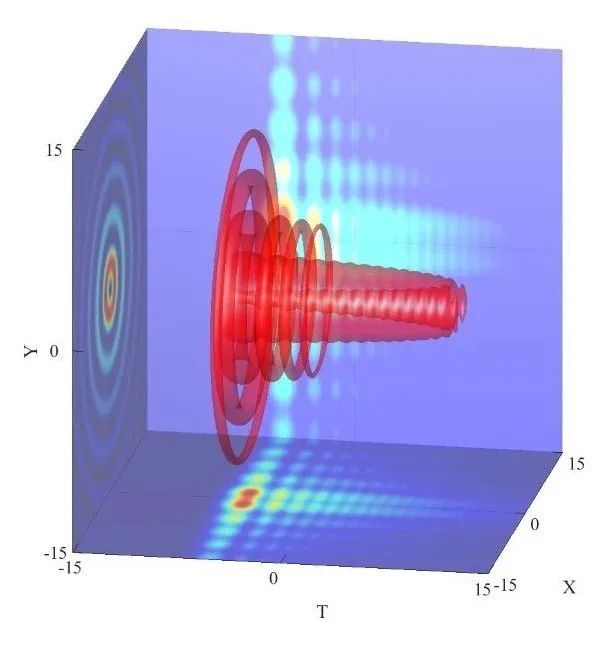
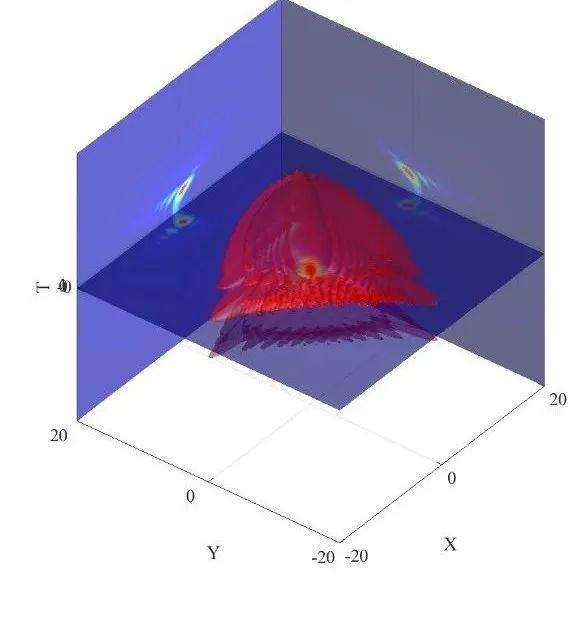
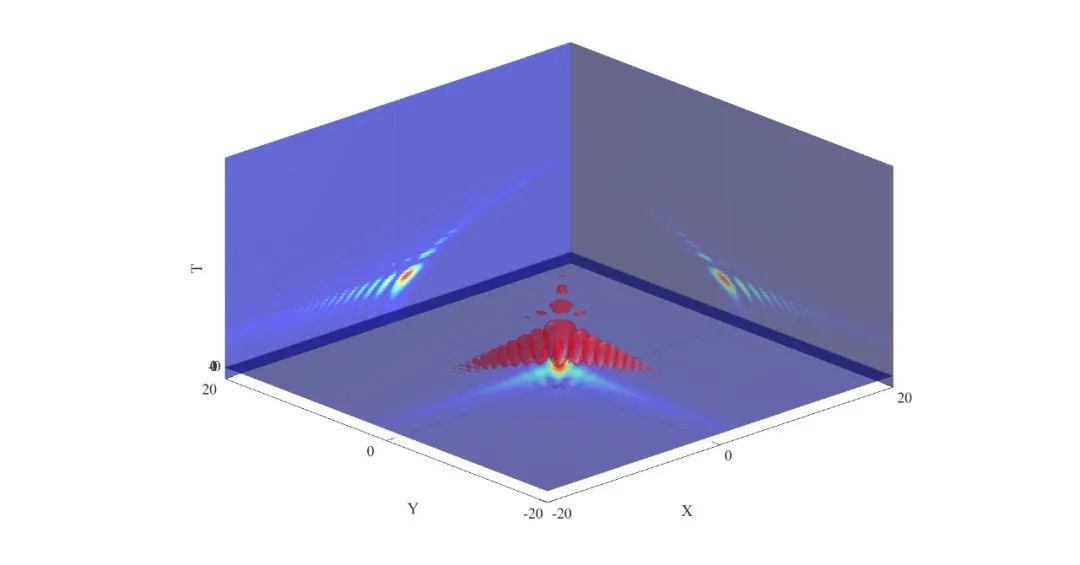
clc;
clear;
close all
%%  产生具有横向OAM的时空涡旋光波包
L0 = 15; t0= 15;
x = linspace(-L0,L0,200); 
y = x'; 
t = linspace(-t0,t0,200);
[T,X,Y] = meshgrid(t,x,y);
[theta,R] = cart2pol(X,Y);
 a = 0.1;b = 5; m = 1; q = 0.02;
lambda = 1/2;
E = besselj(m,R).*airy(-T-b^2/4+1i*a*b).*((1-q)*exp(1i*m*theta)+q.*exp(-1i*m*theta)).*exp(-a*T-1/4*a*b.^2+1i*(lambda*b-1/24*b^3+1/2*a^2*b-1/2*T*b));
I = E.*conj(E); I = I./max(max(max(I)));
scrsz = get(0,'screensize');
figure('Position',[0,0,scrsz(3),scrsz(4)])
hiso = patch(isosurface(T,X,Y,I,0.138));isonormals(T,X,Y,I,hiso) %平滑colormap('pink')hiso.FaceColor = 'red';
 %等值面上色
hiso.EdgeColor = 'none';hiso.FaceAlpha = 0.3;
daspect([1,1,1])view(-10,10);
axis tight
xlabel('T');
ylabel('X');
zlabel('Y')
grid on;
hold on
%% 打光
camlight('headlight');
lighting gouraud;
camlight('right');
lighting gouraud; 
alpha(0.3)
axis([-L0 L0 -L0 L0 -t0 t0])
set(gca,'TickDir','in','Fontname','times new roman','fontsize',20)
set(gca,'xtick',-L0:L0:L0,'xticklabel',ceil(-L0:L0:L0),'ytick',-L0:L0:L0,'yticklabel',ceil(-L0:L0:L0),'ztick',-t0:t0:t0,'zticklabel',ceil(-t0:t0:t0))
%% 平面投影
% XT平面投影%
I1 = I(floor(end/2),:,:); 
%% 截面投影 
XTI1 = sum(I(:,:,:),1); 
I1 = I1./max(max(I1)); 
%% 沿着第一维度求和的投影 （XT面）
%I2 = I(:,floor(end/2),:); 
%% 截面投影 
YTI2 = sum(I(:,:,:),2); I2 = I2./max(max(I2)); 
%% 沿着第二维度求和的投影 （YT面）
%I3 = I(:,:,floor(end/2)); 
%% 截面投影 
XYI3 = sum(I(:,:,:),3); 
I3 = I3./max(max(I3)); 
%% 沿着第三维度求和的投影 （XY面）
[XT_T, XT_X] = meshgrid(t,x); h1 = surf(XT_X,L0*ones(size(XT_T)),XT_T,squeeze(I1),'EdgeColor','none');
colormap('jet')% YT平面投影
[YT_Y,YT_T] = meshgrid(t,y);
h2 = surf(-L0*ones(size(YT_T)),YT_T, YT_Y,squeeze(I2),'EdgeColor','none');
colormap('jet')% XY平面投影
[XY_Y,XY_X] = meshgrid(y,x);
h3 = surf(XY_Y,XY_X,-t0*ones(size(XY_Y)),squeeze(I3),'EdgeColor','none');
colormap('jet')
set(h1,'Facealpha',0.6);
set(h2,'Facealpha',0.6);
set(h3,'Facealpha',0.6);