数据结构复习笔记5.5：二叉平衡树

SGCGYU_Tan

已于 2024-06-07 00:14:03 修改

阅读量1.7k

点赞数 47

分类专栏：数据结构笔记文章标签：数据结构笔记 c++

于 2024-06-06 23:56:32 首次发布

本文链接：https://blog.youkuaiyun.com/2301_81070376/article/details/139512292

版权

笔记同时被 2 个专栏收录

13 篇文章

订阅专栏

数据结构

12 篇文章

订阅专栏

1.为什么要有二叉平衡树

由上一节笔记，我们学习了二叉排序树，知道了他的缺点，当二叉排序树是一棵斜树的时候，插⼊和删除操作的时间复杂度将可能变为O（n）。⼆叉搜索树的查找效率取决于树的高度，因此保持树的⾼度最⼩，即可保证树的查找效率。

2.二叉平衡树

AVL树是最早被发明的⾃平衡⼆叉查找树。在AVL树中，任⼀节点对应的两棵⼦树的最⼤⾼度差为 1，因此它也被称为⾼度平衡树。查找、插⼊和删除在平均和最坏情况下的时间复杂度都是 O(logn）。增加和删除元素的操作则可能需要借由⼀次或多次树旋转，以实现树的重新平衡。

定义：

平衡⼆叉查找树：简称平衡⼆叉树。

由前苏联的数学家 Adelse-Velskil 和 Landis 在 1962 年提出的⾼度平衡的⼆叉树，根据科学家的英⽂名也称为 AVL 树。它具有如下⼏个性质：

1、可以是空树。

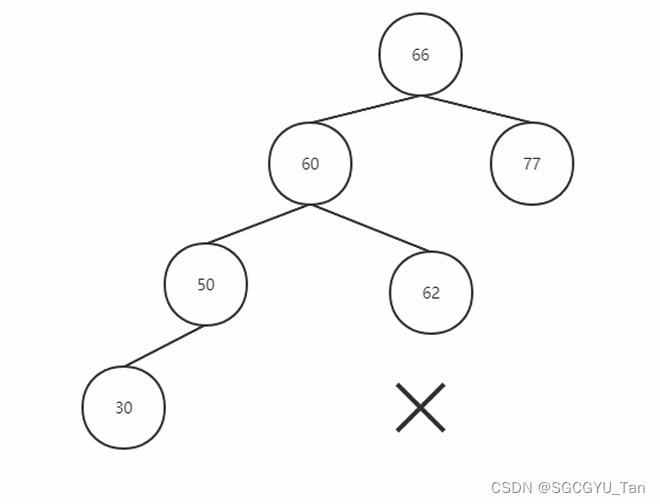
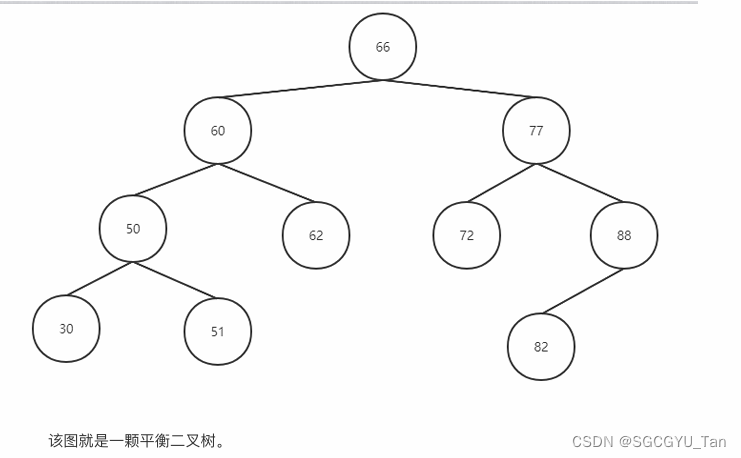
2、假如不是空树，任何⼀个节点的左⼦树与右⼦树都是平衡⼆叉树，并且⾼度之差的绝对值不超过 1。

如图：

3.平衡因子

某节点的左⼦树与右⼦树的⾼度(深度)差即为该节点的平衡因⼦（BF,Balance Factor），平衡⼆叉树中不存在平衡因大于 1 的节点。在⼀棵平衡⼆叉树中，节点的平衡因⼦只能取 0 、1 或者 -1 ，分别对应着左右⼦树等⾼，左⼦树⽐较⾼，右⼦树⽐较⾼。

4.代码展示

1.结点结构

typedef struct AVLnode
{
	int data;
	struct AVLnode * l;
	struct AVLnode * r;
	int h;
}AVLNode,*AVLTree;

2.插入操作

1.先查找同BST
2.后插入：

①先执行BST的插入操作

//递归版本 get_h是获得结点高度的函数
AVLTree AVL_insert(AVLTree ro, int k)
{
	if (ro == NULL)
	{
		AVLNode *s = new AVLNode;
		s->data = k;
		s->l = s->r = NULL;
		s->h = 1;
		return s;//递归尽头
	}
	if (k < ro->data)
	{
		ro->l = AVL_insert(ro->l, k);
		//有可能导致ro左子树的高度-右子树的高度>1
		if (get_h(ro->l) - get_h(ro->r) > 1)
		{
			//失衡 判断LL还是LR
			AVLNode * n = ro->l;
			if (n->data > k)
			{
				//LL 此时失衡结点是ro
				ro = LL_rotation(ro);

			}
			else
			{
				//LR
				ro = LR_rotation(ro);
			}
		}
	}
	else
	{
		ro->r = AVL_insert(ro->r, k);
		if (get_h(ro->r) - get_h(ro->l) > 1)
		{
			//失衡 判断RR还是RL
			AVLNode * n = ro->r;
			if (n->data < k)
			{
				//RR 此时失衡结点是ro
				ro = RR_rotation(ro);

			}
			else
			{
				//RL
				ro = RL_rotation(ro);
			}
		}
	}
	ro->h= Max(get_h(ro->l), get_h(ro->r)) + 1;
	return ro;
}

②判断有没有失衡结点，若有则调整为平衡状态
调整方式为左右旋转

0.旋转操作展示

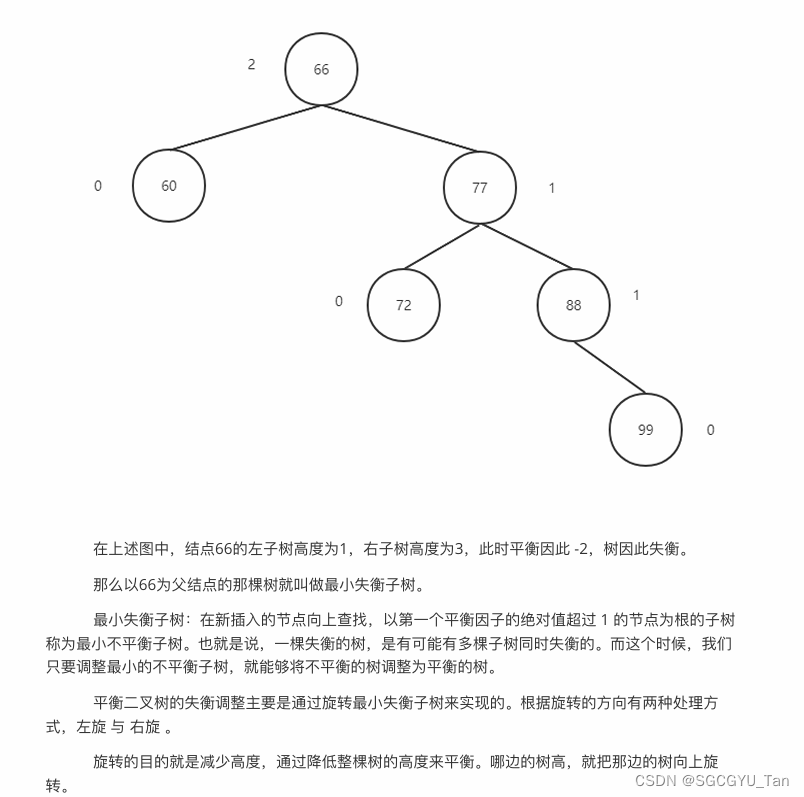
左旋：

以上图为例，加⼊新节点 99 后，节点 66 的左⼦树⾼度为 1，右⼦树⾼度为 3，此时平衡因⼦为 -2。为保证树的平衡，此时需要对节点 66 做出旋转，因为右⼦树⾼度⾼于左⼦树，对节点进⾏左旋操作，流程如下：

1、结点的右孩⼦结点替代此结点的位置

2、右孩⼦的左⼦树变成该结点的右⼦树

3、结点本身变成右孩⼦的左⼦树

右旋：

右旋操作与左旋类似，操作流程为：

1. 节点的左孩⼦代表此节点

2. 节点的左孩⼦的右⼦树变为节点的左⼦树

3. 将此节点作为左孩⼦节点的右⼦树。

假设⼀颗AVL树的某个节点为A，有四种操作会使得A的左右⼦树⾼度差⼤于1，从⽽破坏AVL树的平衡。平衡⼆叉树的插⼊有以下四种情况。

1.LL平衡旋转

//调整函数
AVLTree LL_rotation(AVLTree x)//LL是指左子树左孩子，右旋
{
	AVLNode * y = x->l;
	x->l = y->r;
	y->r = x;
	x->h = Max(get_h(x->l), get_h(x->r)) + 1;
	y->h = Max(get_h(y->l), get_h(y->r)) + 1;
	return y;
}

2.RR平衡旋转


AVLTree RR_rotation(AVLTree x)//LL是指右子树右孩子，左旋
{
	AVLNode * y = x->r;
	x->r = y->l;
	y->l = x;
	x->h = Max(get_h(x->l), get_h(x->r)) + 1;
	y->h = Max(get_h(y->l), get_h(y->r)) + 1;
	return y;
}

3.LR平衡旋转


AVLTree LR_rotation(AVLTree x)
{
	x->l = RR_rotation(x->l);
	x = LL_rotation(x);
	
	return x;
}

4.RL平衡旋转

AVLTree RL_rotation(AVLTree x)
{
	x->r = LL_rotation(x->r);
	x = RR_rotation(x);

	return x;
}

5.总结

1. 在所有的不平衡情况中，都是按照先寻找最⼩不平衡树，然后寻找所属的不平衡类别，再根据 4 种类别进⾏固定化程序的操作。

2. LL , LR ，RR ，RL其实已经为我们提供了最后哪个节点作为新的根指明了⽅向。如 LR 型最后的根节点为原来的根的左孩⼦的右孩⼦，RL 型最后的根节点为原来的根的右孩⼦的左孩⼦。只要记住这四种情况，可以很快地推导出所有的情况。

3. 维护平衡⼆叉树，最麻烦的地方在于平衡因⼦的维护。⼀定要多画。多理解。

3.删除操作

AVL树的删除操作和二叉排序树的删除操作相同，只是多了确保平衡因子的操作。

都分成了四种情况：

1. 删除叶⼦结点

2. 删除的结点只有左⼦树

3. 删除的结点只有右⼦树

4. 删除的节点既有左⼦树⼜有右⼦树只不过对于AVL树来说，你要删除⼀个结点后需要重新检查平衡性并修正。同时，删除操作与插⼊操作后的平衡修正区别在于，插⼊操作后只需要对第⼀个⾮平衡节点进⾏修正，⽽删除操作需要修正所有的⾮平衡结点。

删除操作的⼤致步骤如下：以前三种情况为基础尝试删除节点，并将访问节点⼊栈。

如果尝试删除成功，则依次检查栈顶节点的平衡状态，遇到⾮平衡节点，即进⾏旋转平衡，直到栈空。

如果尝试删除失败，证明是第四种情况。这时先找到被删除节点的右⼦树最⼩节点并删除它，将访问节点继续⼊栈。

再依次检查栈顶节点的平衡状态和修正直到栈空。

对于删除操作造成的⾮平衡状态的修正，可以这样理解：对左或者右⼦树的删除操作相当于对右或者左⼦树的插⼊操作，然后再对应上插⼊的四种情况选择相应的旋转就好了。

//删除
//1.先执行BST删除操作
//2.x的长辈可能失衡 此时先调整最小失衡子树
//调整： 1.左边删除相当于（右边h-左边h 增大了1）右边插入 2.右边删除相当于（左边h-右边h 增大了1）左边插入
//谁失衡了它就是三个结点中最高的点
//左边删除：失衡结点的右孩子r，r的右子树高度>=r左子树高度(RR) r的右子树高度<r的左子树高度(RL)
//右边删除：失衡结点的左孩子l，l的左子树高度>=l右子树高度(LL) l的左子树高度<r的右子树高度(LR)


AVLNode* find_re(AVLNode *p)//找到某结点的前驱
{
	while (p->l != NULL)
	{
		p = p->l;
	}
	return p;
}

AVLTree AVL_delete(AVLTree ro, int x)
{
	if (ro == NULL)
	{
		return NULL;
	}
	if (x < ro->data)
	{
		ro->l = AVL_delete(ro->l, x);
		//删除就可能存在失衡(失衡结点是ro->l)
		if (get_h(ro->r) - get_h(ro->l) > 1)
		{//RR RL
			AVLNode * t = ro->r;
			if (get_h(t->r) >= get_h(t->l))
			{//RR
				ro = RR_rotation(ro);
			}
			else
			{//RL
				ro = RL_rotation(ro);
			}
		}
	}
	else if (x > ro->data)
	{
		ro->r = AVL_delete(ro->r, x);
		if (get_h(ro->l) - get_h(ro->r) > 1)
		{//LL LR
			AVLNode * t = ro->l;
			if (get_h(t->l) >= get_h(t->r))
			{//LL
				ro = LL_rotation(ro);
			}
			else
			{//LR
				ro = LR_rotation(ro);
			}
		}
	}
	else
	{
		if (ro->l != NULL &&ro->r != NULL)
		{
			//度为2
			//找后继
			AVLNode * re = find_re(ro->r);
			ro->data = re->data;
			ro->r = AVL_delete(ro->r, re->data);//以ro->r为根的子树中删除值为re->data的结点
			if (get_h(ro->l) - get_h(ro->r) > 1)
			{//LL LR
				AVLNode * t = ro->l;
				if (get_h(t->l) >= get_h(t->r))
				{//LL
					ro = LL_rotation(ro);
				}
				else
				{//LR
					ro = LR_rotation(ro);
				}
			}
		}
		else
		{
			AVLNode * s = ro;
			//度为1或0
			if (ro->l == NULL)
			{
				ro = ro->r;
			}
			else
			{
				ro = ro->l;
			}
			delete s;
			s = NULL;
			
		}
	}
	if (ro != NULL)//root为空时不需要计算高度
	{
		ro->h = Max(get_h(ro->l), get_h(ro->r)) + 1;
	}
	return ro;
}

5.算法分析

本⽂主要介绍了平衡⼆叉树的相关内容，AVL平衡⼆叉树很好的解决了⼆叉搜索树在遇到有序序列性能退化为O（N）的情况，使得在最坏情况下的搜索效率仍然能够达到O（logN），但这种优化是牺牲了插⼊和删除的性能换来的，故⽽AVL树并不适合需要频繁插⼊和删除的场景，⽽红黑树则是权衡了这种情况，其并不强调严格的平衡性，⽽是保持⼀定的平衡性，从⽽使得在搜索，插⼊，删除的场景下均有⼀个不错的速度，这个会在后续的学习中分析